BME100 f2014:Group20 L2

BME 100 Fall 2014	Home People Lab Write-Up 1 | Lab Write-Up 2 | Lab Write-Up 3 Lab Write-Up 4 | Lab Write-Up 5 | Lab Write-Up 6 Course Logistics For Instructors Photos Wiki Editing Help
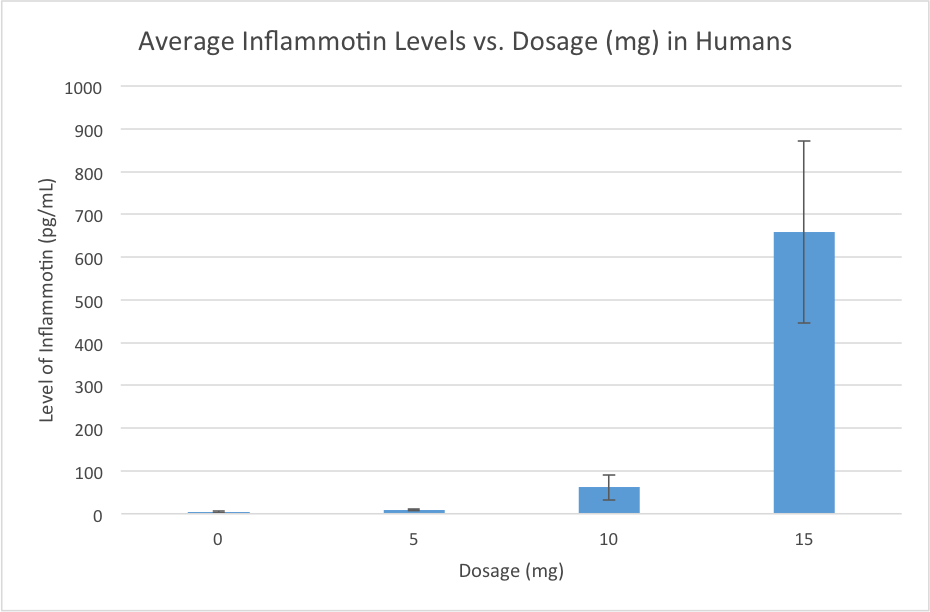
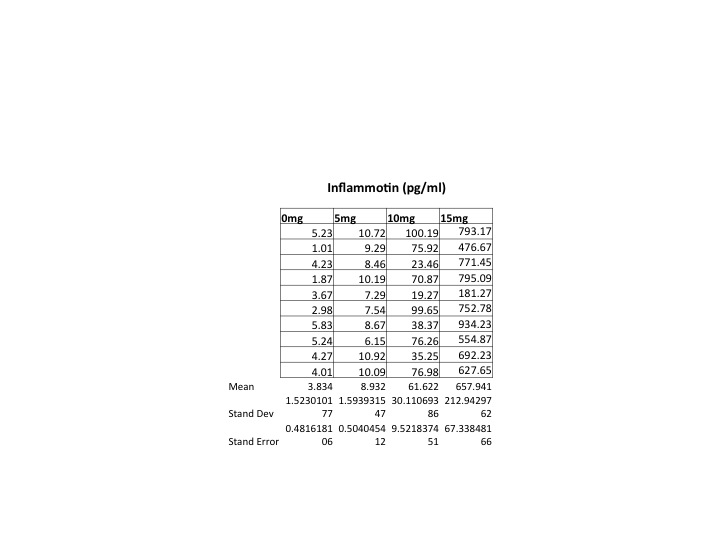
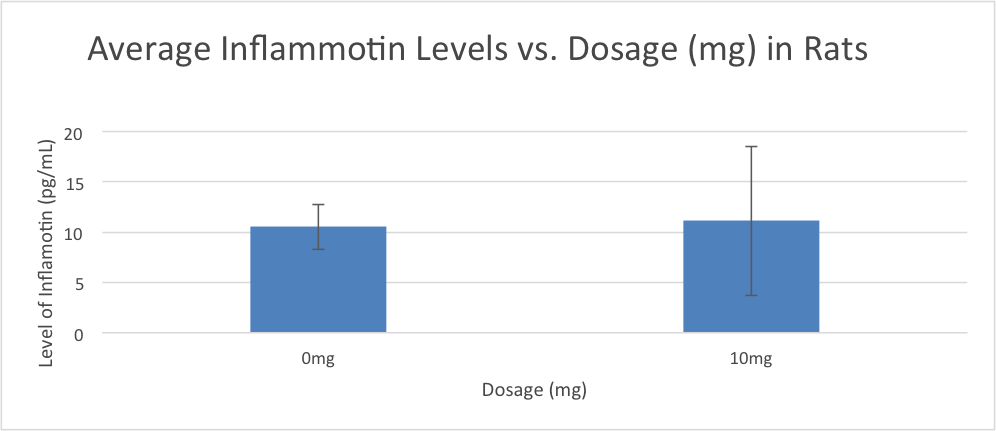
OUR TEAM Ryan Giudice Jeremy Ellis Connor Seiferth Bjorn Houman Karthik Nambiar Name: Your name LAB 2 WRITE-UP Descriptive Statistics Human Trial Average Inflammotin Level= 183.08 pg/ml Average per Dose- 0 mg= 3.834 pg/ml 5 mg= 8.932 pg/ml 10 mg= 61.622 pg/ml 15mg= 657.941 pg/ml Standard Deviation= 6.023 Standard Deviation per Dose- 0 mg= 1.52 5 mg= 1.59 10 mg= 30.11 15 mg= 212.95 Standard Error= 46.98 Standard Error per Dose- 0 mg= 0.48 5 mg= .50 10 mg= 9.5 15 mg= 67.34 Rat Trial Average Inflammotin Level= 10.81 pg/ml Average per Dose- 0 mg= 10.52 pg/mg 10 mg= 11.11 pg/mg Standard Deviation= 5.16 Standard Deviation per Dose- 0 mg= 2.23 10 mg= 7.40 Standard Error= 1.6 Standard Error per Dose- 0mg= .995 10mg= 3.31 Graphs Human Trials Results ‎Rat Trials Results 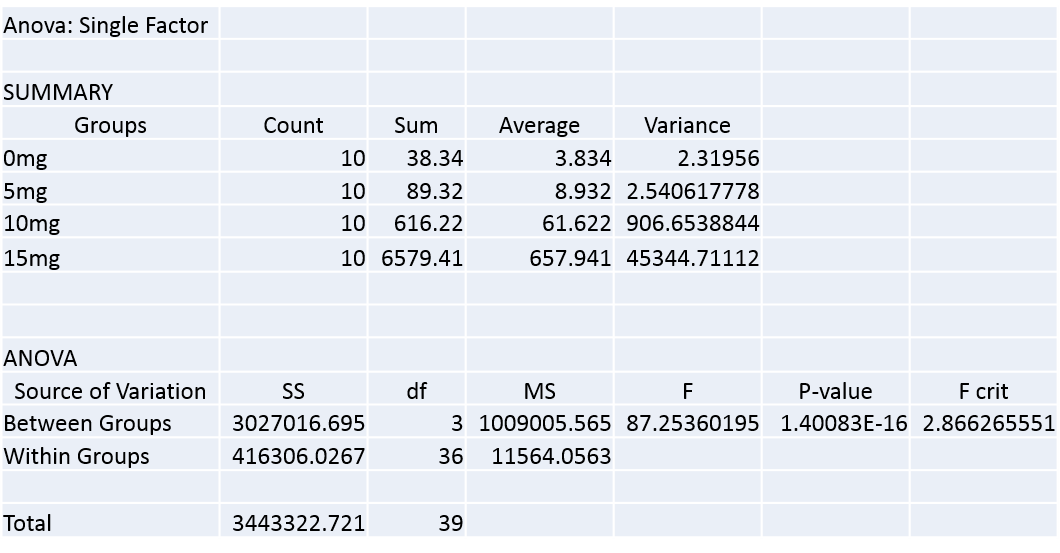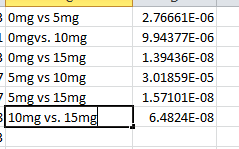Inferential Statistics ANOVA of Human Trials ANOVA Post Test We see from the 1-way ANOVA that the p-value of 1.4*10^-16 fell well under .05 (the standard threshold for rejecting the null hypothesis), and that the F statistic is large. These are both signs of significant variance and reason to reject the null hypothesis (which is that Lipopolysaccharide has no effect on the level of Inflammotin). Unfortunately however, these do not tell us which of the relationships between adjacent doses are significant. To check for that, a Bonferroni Correction is done (as shown in the picture), which in essence, is a t-test for each of the groups. For it to be statistically sound, p-value for Bonferroni must be below (.05)(#samples), or in this case, .0125. This is a characteristic shared by all 2 groups, or in other words, all relations are significant. T.Test of Rat Trials P-value = 0.8120 Our p-value is not less than 0.05 and indicating the difference between groups isn't statistically significant. Summary/Discussion The drug, Lipopolysaccharide, had a significant effect on the subjects in the human experiment; when the doses passed the 5mg mark, the relationship between doses and Inflammotin levels appeared to be exponential, as the growth of the Inflammotin levels increased at a significantly higher rate for every subsequent addition of 5mg to the previous dose. The p-value we calculated from the 1-way ANOVA test of the relationship between dosage and the Inflammotin levels in humans is 1.11 x 10^-16, and that value being so small indicates a statistically significant relationship between the dosage and Inflammotin levels. Regarding the rat experiment, the Inflammotin levels did not seem to have any correlation to doses did, however, it should be noted that the standard deviation was much larger in the 10mg experiment compared to the 0mg. This means that when rats are given LPS, their Inlammotin levels will likely stray from their natural levels. The-p value calculated for the rat experiment was 0.8120; because the p-value is greater than the standard 0.05, there is no statistical difference between groups. In this test, the mean of Inflammotin levels in the rats minutely increased between no dose and the highest dose by 6% , whereas, in the human experiment it increased by a whopping 17061%; indication that there was a significantly different result from the two tests. This might suggest some intrinsic difference in rat biochemistry and human biochemistry, perhaps even an issue of scaling that is not easily perceived right now. This leads us to believe that it might also be age-related, and reduced amount of Inflammotin in the elderly could allow for larger growths as shown in the graphs. Perhaps, for this reason, rat age might have been necessary to measure to show the issues properly. It becomes important to note the ages of the patients in the human test and whatever effect that could have caused. While those prescribed 0 mg had a mean of 70 years old and a Std. Dev of 4.372, 5 mg had 67.44 +/03.643822 yo, 10 mg had 68+/- 8.02772972 yo, and 15 mg had 69.6 +/- 7.40535521 yo. This shows that in general the patient group was good, in that they all were of similar age. It's forth noting that some of the higher groups had higher age variance, which might explain some part of the higher standard deviations in that case.