User:Ginevra Cochran/Formal Report/Final Draft
Steve Koch 23:27, 14 December 2010 (EST):Overall, very nice report! Many great additions from the rough draft and good idea for the new way to take data.
The Balmer series: Determining the Rydberg constant for hydrogen and deuterium
Experimentalists: Ginevra Cochran and Cristhian Carrillo
Junior Laboratory, Department of Physics & Astronomy, University of New Mexico
1919 Lomas Blvd NE
Albuquerque, NM 87131
serenity@unm.eduAbstract
SJK 22:49, 14 December 2010 (EST)

Very nice abstract
The Balmer series is the set of spectral lines produced by the transition of orbital electrons to the second energy level from above it. The Rydberg constant, the most precisely measured quantity in quantum mechanics (Pohl et al, [3]), can be determined from the wavelengths of these spectral lines. We measured these wavelengths using a constant-deviation spectrometer and obtained a Rydberg constant for hydrogen of 1.103(4) * 107 1/m, with an error of 0.6% from the accepted value for hydrogen. For deuterium, we obtained a Rydberg constant of 1.100(2) * 107 1/m, with an error of 0.2% from the accepted value for deuterium. The accepted values for the Rydberg constant of hydrogen and deuterium differ slightly, but our experiment was not precise enough to reliably detect this difference.
Introduction
SJK 23:00, 14 December 2010 (EST)

Excellent introduction.
The Balmer series is the set of spectral lines produced by the transition of orbital electrons to the second energy level from above it. The Rydberg constant can be determined from the wavelengths of these spectral lines and used to find the wavelengths of invisible spectral lines.
Johannes Rydberg, a Swedish physicist, presented the Rydberg formula in the 1880s as a relation between wavelength and differing integers (Martinson and Curtis [8]).
- [math]\displaystyle{ \frac{1}{\lambda} = R_\infty \left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right) }[/math]
This relation was determined experimentally and predated the discovery of quantum mechanics. The Balmer series is the set of spectral lines produced by the Rydberg formula for n2=2, which led to the prediction of non-visible spectral lines (Banet, [5]).
- [math]\displaystyle{ \frac{1}{\lambda} = R_\infty \left(\frac{1}{n_1^2}-\frac{1}{4}\right) }[/math]
Hydrogen has four easily visible spectral lines, and deuterium has three - the fourth is too faint to be measured with much accuracy, and so we did not attempt it.
The measurement of the Rydberg constant has become more and more sophisticated with the passage of time. In 1914, Curtis [11] utilized a hydrogen vacuum tube, a large concave grating, and photography to make measurements of the Balmer series spectrum, and by 1940, Drinkwater et al [2] had constructed an apparatus called a reflexion echelon which could be kept in an evacuated chamber, had two plane mirrors, and could be used to measure wavenumbers (and thus the Rydberg constant) more accurately. A tremendous improvement in the technique used to measure the Rydberg constant came in 1974, when Hänsch et al [6] used a saturation spectrometer (involving a dye-laser) and a Fabry Perot interferometer in a novel approach. In 1981, this experiment had been further refined by Amin et al [7]. The use of crossed-beam spectroscopy, a laser at right angles to the hydrogen beam, which has been substantially heated, contributed to the success of this method, as did the use of an addition Fabry Perot interferometer to regulate and stabilize the cross-laser. As stated in Jentschura et al's 2010 paper [10], the observation of circular Rydberg states in hydrogen-like ions may be used in an even more accurate future determination of the Rydberg constant. According to CODATA [9], the currently accepted value of the Rydberg constant is 10973731.568527(73) m-1.
In this report we will measure the Rydberg constants for hydrogen and deuterium using a Constant-Deviation Spectrometer and hydrogen, deuterium, and mercury spectrum tubes, calibrating the spectrometer for each individual wavelength by adjusting the interior prism manually. We will also attempt to determine whether this method and equipment is capable of distinguishing between the two isotopes' Rydberg constants.
Methods
SJK 23:05, 14 December 2010 (EST)

Excellent methods



Calibration of the constant-deviation spectrometer using mercury
Before commencing our measurements, we adjusted the Adam Hilger, London, Constant-Deviation Spectrometer (SER #12610) to suit the vision of the experimenters. We focused the cross-hairs by adjusting the position of the ocular and focused at the slit using the large knob near the center of the apparatus, eliminating parallax between the two. We elevated the Electro-Technic Products Spectrum Tube Power Supply (Model SP200, 5000V, 10 mA) to align the narrow section of the our spectrum tubes with the slit which allowed light to enter the prism at the center of the Constant-Deviation Spectrometer (see Figure 1). We slotted an Electro-Technic Products mercury spectrum tube (S-68755-30-K) into the Spectrum Tube Power Supply. We switched on the Spectrum Tube Power Supply and allowed it to heat for 5 minutes. We then opened the slit as wide as possible, focused on a spectral line, and narrowed the slit until the line was as sharp as possible without disappearing (see Figure 3). We adjusted the screw drive to the first red wavelength listed in Table 1, removed the cover of the Constant-Deviation Spectrometer's prism (as in Figure 2), and loosened the screw holding it in place, rotating the prism until the given line is directly in the cross-hairs of the Constant-Deviation Spectrometer's ocular. We then retightened the screw securing the prism, returned the cover to the prism, and replaced the mercury spectrum tube with an Electro-Technic Products hydrogen spectrum tube (S-68755-30-G).
We used these values to calibrate the constant-deviation spectrometer, obtained from Gold [1].
Color Accepted Wavelength (nm) Violet (very hard to see) 404.7 Violet 435.8 Weak Blue-Green 491.6 Green 546.1 Yellow 1 577.0 Yellow 2 579.0 Red 690.75
Measurement of the Balmer spectrum of hydrogen and deuterium
We took five measurements of the red spectral line for hydrogen, making sure to turn the screw drive a quarter-turn right past the line before each successive measurement to avoid gear backlash. We then removed the hydrogen spectrum tube from the Spectrum Tube Power Supply and replaced it with an Electro-Technic Products deuterium spectrum tube (S-68755-30-E), where we made the same series of measurements. We repeated the prism calibration of the Constant-Deviation Spectrometer with the mercury spectrum tube for one blue-green and two violet wavelengths, and recorded five measurements of each spectral line for hydrogen and deuterium, with one exception. Deuterium has only one violet spectral line, so we did not attempt to measure the second.
Calculation of the Rydberg constant
We averaged our measured wavelengths for each color and element and used Equation 1 to find the Rydberg constant for each average wavelength.
- Equation 1:
- [math]\displaystyle{ \frac{1}{\lambda }=R(\frac{1}{2^2}-\frac{1}{n^2}), n=3,4,5,6\,\! }[/math]
or
- [math]\displaystyle{ R = \frac{\frac{1}{\lambda }}{(\frac{1}{2^2}-\frac{1}{n^2})}, n=3,4,5,6\,\! }[/math]
The accepted Rydberg constant is derived from quantum mechanics and has the following formulation:
- [math]\displaystyle{ R=\frac{\mu e^4}{8\epsilon _0^2ch^3}\,\! }[/math]
- Where [math]\displaystyle{ \mu\,\! }[/math] is the reduced mass.
[math]\displaystyle{ \mu = \frac{m_e*M}{m_e+M}\,\! }[/math] where M is the mass of the nucleus, as in Coffman [4].
We calculated our percent error for hydrogen's and deuterium's Rydberg constants using this formula and the definition of percent error:
- [math]\displaystyle{ \% error=\frac{R_{accepted}-R_{measured}}{R_{accepted}} }[/math]
All these calculations took place in Google Docs, using the SUM, ABS, STDEV, and SQRT functions, in addition to basic arithmetic.
Results and Discussion
SJK 23:11, 14 December 2010 (EST)

Nice addition of figures and captions. I don't agree with the linear fits. I like the additional figure to show the overlap of the hydrogen and deuterium measurements.
Element Accepted Rydberg constant (1/m) Calculated average Rydberg constant (1/m) SEM of calculated constant percent error Hydrogen 1.0967*107 1.103*107 0.004*107 0.6% Deuterium 1.0971*107 1.100*107 0.002*107 0.2%
- Our calculations are visible here, and our raw data here. SJK 23:07, 14 December 2010 (EST)

23:07, 14 December 2010 (EST)
I think these accidentally link to the same sheet
Also for the figures, it's not really supposed to be a linear relationship, unless you plot 1/lambda versus the 1/n^2-1/n^2 factor
-
Figure 4: Hydrogen. The Balmer series wavelengths versus corresponding quantum numbers.
The best-fit line shows the linear nature of the relationship between wavelength and quantum number. -
Figure 5: Deuterium. The Balmer series wavelengths versus corresponding quantum numbers.
The best-fit line shows the linear nature of the relationship between wavelength and quantum number.
- Figures 4 and 5 show the measured wavelengths (in nanometers) of hydrogen and deuterium versus the Balmer series' quantum numbers, as well as their best-fit lines. Error bars were added to these figures, but our standard errors of the mean were so small that they did not show up well in these figures. Figures 4 and 5 do demonstrate, however, the linear nature of the relationship between quantum number and wavelength, which bears out our measurement of the Rydberg constant.
'x' indicated hydrogen data, 'o' indicated deuterium data.
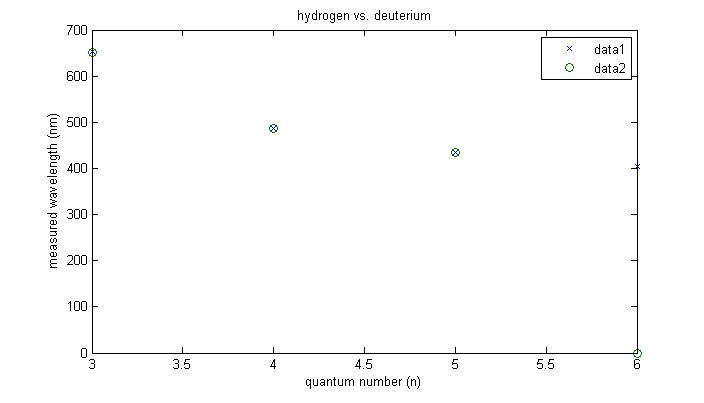
- Figure 6 shows the wavelengths (in nanometers) for hydrogen and deuterium together versus the Balmer series' quantum numbers. Hydrogen is indicated by an 'x', deuterium by an 'o'. As in Figures 4 and 5, it is not evident from this graph exactly how the two isotopes compare,though they seem very close.
Each trio of markers indicates an average wavelength plus and minus a standard error of the mean; red 'x's are hydrogen data, blue 'o's are deuterium.
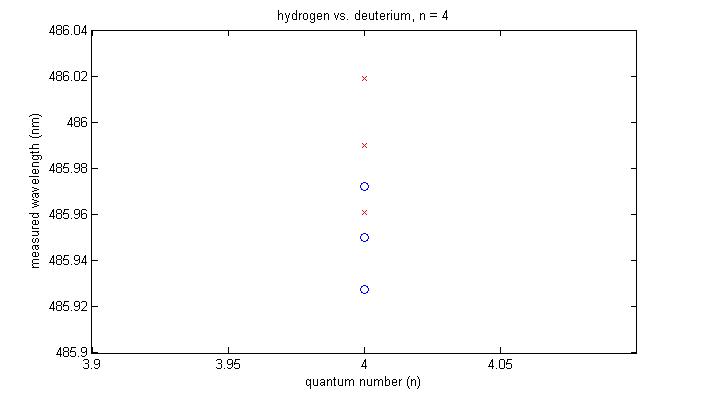
- Figure 7 shows the average wavelength and standard errors of the mean for hydrogen and deuterium at n = 4. The red 'x's are hydrogen data, blue 'o's are deuterium. Each trio of markers consist of an upper and lower error bar and a central average wavelength. We observed that the lower error bar for hydrogen overlapped with the upper error bar for deuterium, showing that our instrument and experiment were not precise enough to detect the difference in the wavelengths or Rydberg constants for hydrogen and deuterium.
Conclusions
The values we obtained in this experiment were very close to the accepted values, as seen in Table 2. Figures 4, 5, and 6 show the linear nature of the relationship between emitted wavelength and level of quantum transition, confirming that the Rydberg constant is indeed a constant. The error inherent in the equipment and experiment prevented us from being able to reliably distinguish between the Rydberg constant for hydrogen and deuterium (as seen in Figure 7), because our standard error of the mean were wide enough that they overlapped for the two isotopes. This may have been partly due to the similarity of their masses. Further experimentation comparing the hydrogen constant of hydrogen to that of sodium, for example, could be enlightening as to the exact accuracy of our equipment because the discrepancy in the masses and thus in the accepted Rydberg constants would be larger. We could also take several sets of measurements for the Rydberg constant of hydrogen and compare the differences between them to the difference between the Rydberg constants for hydrogen and deuterium; it seems likely that these two differences would be similar in magnitude.
Acknowledgments
I would like to thank my lab partner, Cristhian Carrillo, Katie Richardson, and Professor Koch for all their help in the execution of this lab and all the other labs this semester, and Alexandra Andrego for the use of her photos documenting the experiment setup. We used Google Docs to calculate our results and MATLAB 7.8.0 (R2009a) to generate Figures 4, 5, 6, and 7. A sample of our MATLAB code is visible here.
References
- [1] Gold, Michael. The University of New Mexico Dept. of Physics and Astronomy PHYSICS 307L: 'Junior Laboratory Manual Fall 2006'. http://www-hep.phys.unm.edu/~gold/phys307L/manual.pdf.
- [2] Drinkwater, J. W.; Owen Richardson; W. Ewart Williams. "Determinations of the Rydberg Constants, e/m, and the Fine Structures of Hα and Dα by means of a Reflexion Echelon". Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences. Vol. 174, No. 957 (Feb. 1, 1940), pp. 164-188. Published by: The Royal Society http://www.jstor.org/stable/97359.
- [3] Pohl, Randolf; Antognini, Aldo; Nex, François; Amaro, Fernando D.; Biraben, François; Cardoso, João M. R.; Covita, Daniel S.; Dax, Andreas et al. (2010). "The size of the proton". Nature 466 (7303): 213–216. doi:10.1038/nature09250.
- [4] Coffman, Moody L. "Correction to the Rydberg Constant for Finite Nuclear Mass". American Journal of Physics 33 (10): 820–823. 1965. doi:10.1119/1.1970992.
- [5] Banet, Leo. "Evolution of the Balmer Series". Am. J. Phys. 34, 496 (1966), DOI:10.1119/1.1973077 http://scitation.aip.org/getabs/servlet/GetabsServlet?prog=normal&id=AJPIAS000034000006000496000001&idtype=cvips&gifs=yes&ref=no.
- [6] Hänsch, T. W.; Nayfeh, M. H.; Lee, S. A.; Curry, S. M.; Shahin, I. S. "Precision Measurement of the Rydberg Constant by Laser Saturation Spectroscopy of the Balmer Line in Hydrogen and Deuterium". Phys. Rev. Lett. 32(24), 1336-1340 (1974).http://prl.aps.org/abstract/PRL/v32/i24/p1336_1.
- [7] Amin, S. R.; Caldwell, C. D.; Lichten, W. "Crossed-Beam Spectroscopy of Hydrogen: A new Value for the Rydberg Constant". Phys. Rev. Lett. 47(18), 1234-1238 (1981). http://prl.aps.org/abstract/PRL/v47/i18/p1234_1.
- [8] Martinson, Indrek; Curtis, L.J. "Janne Rydberg – his life and work". NIM B 235: 17–22. 2005. doi:10.1016/j.nimb.2005.03.137.
- [9] "CODATA Value: Rydberg Constant". The NIST Reference on Constants, Units, and Uncertainty. 2006. http://physics.nist.gov/cgi-bin/cuu/Value?ryd.
- [10] Jentschura, U. D.; Mohr, P. J.; Tan, J. N. "Fundamental constants and tests of theory in Rydberg states of one-electron ions". J. Phys. B 43, 074002, p.5 2010. http://iopscience.iop.org/0953-4075/43/7/074002.
- [11] Curtis, W. E. "Wave-Lengths of Hydrogen Lines and Determination of the Series Constant". Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character. Vol. 90, No. 622 (Sep. 7, 1914), pp. 605-620. Published by: The Royal Society http://www.jstor.org/stable/93534.

