Physics307L F09:People/Andrego/FormalReport
From OpenWetWare
Jump to navigationJump to search
Balmer Series: Observing the Visible Spectra of Hydrogen
Experimentalists: Alexandra S. Andrego & Anastasia A. Ierides
Junior Lab, Department of Physics & Astronomy, University of New Mexico
Albuquerque, NM 87131
aandrego@unm.edu

Abstract
- On June 25th 1884, J.J. Balmer claimed that he could accurately determine the wavelengths of spectral lines of Hydrogen using a series he developed and named the "Balmer Series". The discovery of the quantitative relationship between wavelengths and the Rydberg constant paved the way for further advancement and experimentation in atomic spectrum theory and quantum physics. The Balmer Series lead to the ability to predict spectral lines beyond the observable for hydrogen atoms [4]. The Balmer series can be described as the designation of visible spectral lines of the emission of hydrogen atoms. The Balmer series for the Hydrogen atom contains eight visual spectral lines (32 in total) though only four are observable under the conditions of this experiment [7]. The four observable spectral lines are categorized by Ultra Violet, Violet, Blue-Green, and Red, depending on the value of the light wavelength. The use of a spectrometer allows the observation and classification of spectra lines of the hydrogen atom. By using electrical stimulation to excite the hydrogen atoms to higher energy levels, measurements of the emitted photons with wavelengths equivalent to the energy of our excited electrons can be made. Through such measurements it is possible to experimentally determine Rydberg's constant, R, that is used in the Balmer-Rydberg equation for hydrogen:
- [math]\displaystyle{ \frac{1}{\lambda}=R(\frac{1}{2^2}-\frac{1}{n^2}), n=3,4,5,..\,\! }[/math]
- [math]\displaystyle{ \frac{1}{\lambda}=R(\frac{1}{2^2}-\frac{1}{n^2}), n=3,4,5,..\,\! }[/math]
- In this experiment our data gave us an experimental value of the Rydberg constant to be
- [math]\displaystyle{ R_{experimental mean}\approx1.0973\pm 0.0025\times10^7 m^{-1}\,\! }[/math]
Introduction
- The Rydberg constant, named for Johannes Rydberg, a Swedish physicist, is an important stepping stone for the evaluation of many other fundamental physical constants and spectroscopic transitions [10]. The Rydberg constant is most notable for its contribution to the measurement of absolute wavelengths in spectrum transitions like those found in the Balmer series observed in this report [9]. The Balmer series is one of the most important developments in the field of quantum mechanics. It denotes the discovery of the systematic pattern observed in the wavelengths of the emitted spectrum from hydrogen atoms [11]. The four visible lines of the hydrogen spectrum, described by the Balmer series and the Balmer-Rydberg equation, were first observed and characterized by Bohr using an assumption of quantized orbits in a classical physics argument. Later the introduction and wide acceptance of the Balmer series allowed Neils Bohr to develop his quantum theory of atoms [8]. Five years after Johann Jakob Balmer published his Balmer Series equation for the hydrogen atom, Rydberg, without previous knowledge of Balmer's work, created a more general form of the Balmer equation for different spectra of atoms in alkali metals. The Balmer series is just a special case for the Balmer-Rydberg equation where m (the quantized transition number) is two [12].
- [math]\displaystyle{ \frac{1}{\lambda }=R(\frac{1}{m^2}-\frac{1}{n^2}) }[/math]
- [math]\displaystyle{ m=1,2,3,...\,\! }[/math]
- [math]\displaystyle{ n=2,3,4,5,...\,\! }[/math]
- [math]\displaystyle{ n\gt m\,\! }[/math]
- [math]\displaystyle{ \frac{1}{\lambda }=R(\frac{1}{m^2}-\frac{1}{n^2}) }[/math]
- In this lab we used the Balmer-Rydberg equation to determine experimental values of the Rydberg Constant, R. In this experiment we were able to excite hydrogen and deuterium atoms of vapor form and view their emitted spectrum through the use of a spectrometer. Through analysis of the Balmer-Rydberg equation and the use of a linear fit function on our data we were able to discern two different values of the Rydberg constant, one for the hydrogen spectrum and one for the deuterium spectrum. The deuterium atom contains both a proton and a neutron in its atomic structure, unlike the hydrogen atom of which only carries a proton. This difference in structure also causes there to be a difference in mass between the two particles [9]. In our experimentation we attempted to observe any noticeable difference between our calculated Rydberg constants due to this difference in mass.
Methods



Calibration of the Spectrometer
- To begin this experiment a few preliminary steps were taken to prepare for our experimentation. First we adjusted the Constant-Deviation Spectrometer (SER #12610) by bringing the cross-hairs into focus and sliding the ocular to a position that suited our vision and allowed for no parallax to exist between the cross-hairs and the slit of the spectrometer when it was focused sharply. We brought the slit into focus while looking through the eye piece by turning the large ring near the center of the viewing telescope called the spectrometer dial. We then attached and positioned the mercury bulb (Mercury Vapor Spectrum Tube (S-68755-30-K)) into the spectrum tube power supply (Model SP200) and waited approximately five minutes for the mercury bulb to warm up. Our complete set up can be seen in FIGURE 1. Calibrating the spectrometer is a very important part of the set up for this experiment. The calibration process was made easier by the use of a wide slit setting seen in FIGURE 2. After finding a line of the the mercury spectrum through the eye piece of the spectrometer and narrowing the slit until the line was focused sharply, we were able to use the known values of light wavelengths for the spectral lines of mercury (TABLE 1) to position the prism accurately [2]. The more precise our calibration was the smaller our systematic error was. The positioning of the prism was done by a series of small rotations of the prism and measurements from the spectrometer dial, seen in detail in FIGURE 3. We placed our spectrometer dial on the correct measurement for the spectral line we were observing and then attempted to correctly position our prism so that the corresponding spectral line was aligned on the cross hairs in the eyepiece of the spectrometer with a small slit width. This was best done by starting off with a large slit width and then slowly decreasing its width as we focused in on our spectral line. It is very important to understand the mechanics of a spectrometer to avoid causing unnecessary systematic error. Due to the use of gears in the spectrometer dial, "back lash" caused by the empty space between the teeth of the gears, can cause false data. It is important to always turn the dial back at least a quarter of a turn before rotating to the position at which a measurement needs to be taken. This insures that when the measurement is taken, the gears are continuously in contact and the measurements are more accurate. We repeated this process until the positioning of all components (prism, spectrometer, spectrometer dial, and slit width) yielded the correct measurements for the wavelengths of the corresponding mercury spectral line, for all visible lines. Once the calibration process was complete we were able to remove the mercury bulb and replace it with the hydrogen bulb (Hydrogen Spectrum Tube (S-68755-30-G)), and/or the deuterium bulb (Deuterium Spectrum Tube (S-68755-30-E)), and thus began our experimentation.
TABLE 1
Color Wavelength (nm) Deep Violet (very hard to see) 404.7 Violet 435.8 Very Weak Blue-Green skip this one Green 546.1 Yellow 1 577.0 Yellow 2 579.0 Red 690.75
Measuring the Spectral Lines for Hydrogen and Deuterium
- After replacing the mercury bulb in the experiment with the hydrogen bulb (and again waiting the five minutes to allow the bulb to warm up and keeping in mind the "back lash" effect), we were able to easily take the measurements for the visual spectral lines of hydrogen. We began by rotating the spectrometer dial until a spectral line came into focus through the spectrometer eye piece, we made sure to do this with a wide slit width setting that made the spectral lines more easily viewable. We then narrowed our slit width and rotated our spectrometer dial once more to align the spectral line with cross hairs and to record the measurement. We repeated this process five times for each of the four visible spectral lines for Hydrogen. Anastasia read the measurements off of our spectrometer dial and I did the alignment of each spectral line. Once we felt we had taken sufficient data with the Hydrogen bulb we replaced it with a deuterium bulb and observed and recorded its spectral lines through the same method. Our data taking was spread out over the course of two non consecutive days. All of our hydrogen measurements were taken on the first day of experimentation. However for the Deuterium measurements we had to recalibrate our spectrometer on the second day of experimentation before beginning again. This recalibration could have some effects on our systematic error between our Hydrogen data and our Deuterium data.Our raw data table can be seen in our Primary Lab Notebook [6]. After collecting all of our needed measurements we used the average of all values for each spectral line to determine the best measured wavelength for each spectral color of the respective element. The standard error of mean was calculated to obtain the 68% uncertainty margins for our measurements. Once the average wavelength per spectral line was determined, we took the mean over all spectral lines of the same element and used that average to compute an experimental Rydberg constant ,R, as appears in the Balmer-Rydberg equation discussed earlier in this paper. The use of Microsoft Excel and Google Docs made the analysis of the raw data possible.
Analysis and Results
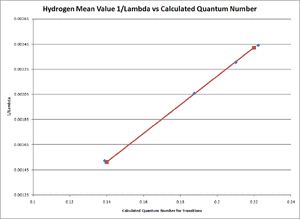
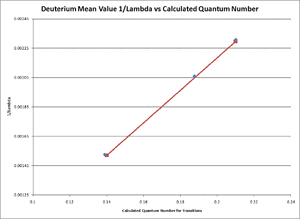
- Our results from this experiment can be seen in TABLE 2 below. The transition column refers to the structure of the Balmer series and the Balmer-Rydberg equation discussed earlier in this paper. All error margins included in the data table are the results of the standard error of mean calculation performed by excel. The excel spreadsheet with these calculations can be refered to in our Primary Lab Notebook under the Analysis section [6].
Error in widget Google Spreadsheet: Unable to load template 'wiki:Google Spreadsheet'
- From the values listed in TABLE 2, a Rydberg's constant was calculated from the Balmer-Rydberg equation as follows:
- [math]\displaystyle{ \frac{1}{\lambda }=R(\frac{1}{2^2}-\frac{1}{n^2}), n=3,4,5,6\,\! }[/math]
- [math]\displaystyle{ \frac{1}{\lambda }=R(\frac{n^2-4}{4n^2})\,\! }[/math]
- [math]\displaystyle{ R=\frac{4n^2}{\lambda(n^2-4)}\,\! }[/math]
- [math]\displaystyle{ \frac{1}{\lambda }=R(\frac{1}{2^2}-\frac{1}{n^2}), n=3,4,5,6\,\! }[/math]
- Where the relationship between [math]\displaystyle{ \frac{1}{\lambda }\,\! }[/math] and the term [math]\displaystyle{ \frac{n^2-4}{4n^2}\,\! }[/math] were graphed using excel and the resulting slope for both the Hydrogen and Deuterium cases was the average experimental value of the Rydberg Constant (see FIGURE 4 for the Hydrogen Linear Fitting and FIGURE 5 for the Deuterium Linear Fitting). Excel was used for the creation of theses graphs and for the linear fit seen on both figures. For any and all excel spreadsheets please refer to our Primary Lab Notebook [6].
- The average values for the measured Rydberg's constants are:
- [math]\displaystyle{ R_{Hydrogen,average}\approx1.0973\pm 0.0025\times10^7 m^{-1}\,\! }[/math]
- [math]\displaystyle{ R_{Deuterium,average}\approx1.0983\pm 0.0007\times10^7 m^{-1}\,\! }[/math]
- We discovered that our experimental Rydberg constant for the Hydrogen Spectrum was approximately off by a small magnitude of the fifth order, and henceforth our experiment proved to be successful in estimating an appropriate value for the Rydberg constant for the Hydrogen Spectrum Balmer Series. However,our experimental mean value for the Deuterium Balmer Series was not as successful. Our uncertainty in our experimental Rydberg constant for the Deuterium spectrum does not put the accepted value in our attained range. This goes to show that our experiement set-up on day two of our data trials (Deuterium data was only taken on the second day of trials and had a different calibration), falls short in statistically minimizing both our random and systematic error. The accepted value of the Rydberg constant, for which we have based all comparisons, is [5]:SJK 13:42, 15 December 2009 (EST)

13:42, 15 December 2009 (EST)
But, that is the constant for an infinitely massive nucleus! You actually want to compare hydrogen to the calculated constant using reduced mass of an electron with one proton, and deuterium to the calculated constant using the reduced mass with one proton and one neutron. You could then comment on whether you could possibly discern this difference with your spectrometer.- [math]\displaystyle{ R_{accepted}=1.0973731568525\times10^7 m^{-1}\,\! }[/math]
Discussion and Conclusion
- In order to fully comprehend the results above, it is beneficial to compare the experimental results with the accepted values. Through such a comparison it is evident that the measured values attained through this experiment were sufficiently close to the accepted value given above. It is evident from results such as these that the systematic error was not completely minimized for this experiment. As stated above, I believe that some of this systematic error could be the result of the two different calibrations for the data taken on the hydrogen spectrum tube versus the data taken for the deuterium spectrum tube. This systematic error could be reduced by retaking data without a second calibration. We did try to achieve this in an extra lab session, but we proved to be unsuccessful in appropriately calibrating our spectrometer. Therefore the extra data was determined to be insufficient in minimizing the systematic error, and was thrown out. In our first two data taking sessions we did not see the need to throw out any of our taken data. When we compared the results from the hydrogen bulb and the deuterium bulb, we noticed that both results had insignificantly different true means for each wavelength of the spectrum and the calculated Rydberg constant. Because our error cannot be said to be minimized any noticeable difference between the true means cannot be said to be purposeful, and hence from our data we cannot discern any difference between the values obtained for hydrogen and deuterium based on their masses. According to the theory behind the Balmer series and Rydberg constant, there should exist a true mean value difference due to the difference in mass that exists between the two atoms, as described above. This should therefore be true for all atoms of varying mass, but was not evident in this experiment.
Acknowledgments
- I would like to extend my greatest gratitude for Anastasia Ierides who was my partner for the Balmer Series Lab. Her enthusiasm and work ethic made this experiment one of my favorites.
- Google Docs and Microsoft Excel were used to format and post our raw data and error analysis to our primary lab notebook and this formal report
- I would also like extend my utmost appreciation to Professor Koch and Pranav for monitoring and providing guidance through this entire process.
References
- [1] 'Hydrogen Energies and Spectrum'. http://hyperphysics.phy-astr.gsu.edu/Hbase/hyde.html#c4
- [2] Gold, Michael. The University of New Mexico Dept. of Physics and Astronomy PHYSICS 307L: 'Junior Laboratory Manual Fall 2006'. http://www-hep.phys.unm.edu/~gold/phys307L/manual.pdf
- [3] Merikanto, 'File:Emission spectrum-H.png'. Wikepedia, May 2006 http://en.wikipedia.org/wiki/File:Emission_spectrum-H.png
- [4] Banet, Leo, 'Evolution of the Balmer Series'. Am. J. Phys. 34, 496 (1966), DOI:10.1119/1.1973077 http://scitation.aip.org/getabs/servlet/GetabsServlet?prog=normal&id=AJPIAS000034000006000496000001&idtype=cvips&gifs=yes&ref=no
- [5] Mohr, Peter J., Taylor, Barry N., and David B. Newell, 'CODATA recommended values of the fundamental physical constants: 2006'. Rev. Mod. Phys. 80, 633 (2008), DOI:10.1103/RevModPhys.80.633 http://physics.nist.gov/cuu/Constants/codata.pdf
- [6] User:Alexandra S. Andrego/Notebook/Physics 307L/2009/09/28, 'Balmer Series'. http://www.openwetware.org/wiki/User:Alexandra_S._Andrego/Notebook/Physics_307L/2009/09/28
- [7] Wood, R. W., 'An Extension of the Balmer Series of Hydrogen and Spectroscopic Phenomena of Very Long Vacuum Tubes'. Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character, Vol. 97, No. 687 (Aug. 3, 1920), pp. 455-470 http://www.jstor.org/stable/93837
- [8] Rigden, John S., James O'Connell, and Reviewer, Am. J., 'Hydrogen: The Essential Element'. American Journal of Physics Phys. 71, 189 (2003), DOI:10.1119/1.1522705 http://scitation.aip.org.libproxy.unm.edu/getpdf/servlet/GetPDFServlet?filetype=pdf&id=AJPIAS000071000002000189000001&idtype=cvips&prog=normal
- [9] Hänsch, T. W., M. H. Nayfeh, S. A. Lee, S. M. Curry, and I. S. Shahin,'Precision Measurement of the Rydberg Constant by Laser Saturation Spectroscopy of the Balmer α Line in Hydrogen and Deuterium'. Department of Physics, Stanford University, Stanford, California 94305. The American Physical Society, Vol 32, 1336-1338. 1974. DOI:10.1103/PhysRevLett.32.1336 http://link.aps.org/doi/10.1103/PhysRevLett.32.1336
- [10] Andreae, T., W. König, R. Wynands, D. Leibfried, F. Schmidt-Kaler, C. Zimmermann, D. Meschede, and T. W. Hänsch, 'Absolute frequency measurement of the hydrogen 1S-2S transition and a new value of the Rydberg constant'. Max-Planck-Institut für Quantenoptik, W-8046 Garching, Germany. The American Physical Society, Vol 69, 1923-1926. 1992. DOI:10.1103/PhysRevLett.69.1923 http://link.aps.org/doi/10.1103/PhysRevLett.69.1923
- [11] Laws, Edward. 'Mathematical Methods for Oceanographers: An Introduction'. John Wiley and Sons Inc. NY, New York. Ed 1, x. 1997. ISBN: 0-471-16221-3.
- [12] Schawlow, Arthur L.. 'Spectroscopy in a New Light'. Department of Physics, Stanford University, Stanford, California 94305. The American Physical Society, Vol 54, 697-707. 1982. DOI: 10.1103/RevModPhys.54.697 http://link.aps.org/doi/10.1103/RevModPhys.54.697