User:David J Weiss/Notebook/people/weiss/Formal
Experimental Determination of the Electron Charge to Mass Ratio
Abstract
The ratio for electric charge to the mass of an electron is a fundamental concept in physics and useful for students interested in the study of physics. From this you can conclude how the electron is hardly effected by gravity and how the electric field governs how the electron behaves. This ratio is important to know because it is one of the most important values in quantum mechanics. We did this by means of observing the trajectory of electrons in a known constant magnetic field. From this observation you can determine the ratio of electric charge to mass for an electron as a function of observed radii, magnetic field, and energy. This can be done using an electron gun, a Helmholtz Coil and a couple of power sources. Using this equipment, we determined how a beam of electrons curves within a magnetic field and thus measured radii and used some mathematical manipulation to find the ratio for electric charge compared to mass for the electrons. From our experimental data, we found that the ratio of e/m is 2.3+/-.23*10 coul/kg. This measurement was within the 68% confidence interval. Our analysis showed some systematic and random errors that were prevalent throughout the experiment. We will later discuss the reasons and sources of these errors.
Introduction
The charge of an electron is one of the most basic concepts in the entire study of electromagnetism and atomic particles. J.J. Thompson was the first person to find an electron in a series of experiments which used cathode ray tubes. He did three different experiments and it wasn't until the third in 1987 that he found the charge to mass ratio for the electron 2. These results led him to formulate his "Plum Pudding Model" of the atom, based on experiments similar to the one detailed here. For these experiments he was awarded the Nobel Prize in Physics in the year 1906.
After Thompson did these experiments, R.A. Millikan discovered through experimentation the charge of the electron. His experiments involved dropping oil droplets in a chamber that could be charged to see how the oil droplets reacted in an electric field. These experiments then led to the discovery of the charge that an electron has on it3. He was later awarded the Nobel Prize in Physics in 1923 for these experiments after some controversy due to Felix Ehrenhaft's claim that he found a smaller charge than Millikan. These claims turned out to be wrong and the prize was given to Millikan.
Without these fundamental experiments, we could have not found the charge of the electron, and without this fundamental constant some of the work would not be possible in chemistry, atomic physics, and quantum mechanics. The experiment that we did was similar to the experiment that Thompson did in that we used an electron gun to "boil" off electrons and measure how they behaved in a magnetic field. We varied the force of the electrons by means of changing the voltage to the electron gun which is the Lorenz Force4 and we varied the magnetic field by means of changing the current applied to the Helmholtz Coils5 to determine how an electron responds to a changing electric field and/or a changing force.
Experiment and Materials
Instrumentation and Assembly
SJK 16:13, 15 December 2009 (EST)

This should also be in past tense. E.g., "The power source was connected to the electron gun."
An electron gun is housed in a bulb containing helium gas that allows the electron beam to be observed. A Helmholtz Coil is attached to this apparatus so that a uniform magnetic field can be generated. Use of this manufactured piece (e/m Experimental Apparatus Model TG-13 Uchida Yoko as shown in Fig. 1) eliminates the need to assemble individual components and properly align them. Three separate power supplies connect to a different part of the e/m apparatus. A connection needs to be made between the 6-9 Vdc 2A power supply (SOAR corporation DC Power Supply Model 7403, 0-36V, 3A, as shown in Fig.3) and the Helmholtz Coil with a multimeter in series (BK PRECISION Digital Multimeter Model 2831B, Fig 3). The 6.3V power supply (Hewlett-Packard DC Power Supply Model 6384A, Fig. 2) is connected to the heater jacks. A power source rated at 150-300V (Gelman Instrument Company Deluxe Regulated Power Supply, Fig.3) is connected to another multimeter (BK PRECISION Digital Multimeter (Model 2831B, Fig. 2) to the electron gun.



Procedure and Methods
We followed the general procedure found in Professor Gold's Lab Manual1. We first turned on the power to the heater and let it warm up for approximately 2 minutes. Our observation of the cathode glowing red indicated it was heated. After we warmed up the heater, we applied a voltage of 200V to the electron gun and we then observed the beam of electrons that was glowing green. A current was applied to the Helmholtz Coils and we observed the electron beam take a circular orbit. We took data on the radii of electron beam, one on the right side and one on the left, in addition to the voltage on the electron gun and the current on the Helmholtz Coils. We collected the data on the radii of the beam by looking at a ruler attached to the back of the e/m apparatus (Fig. 1). We obtained two sets of results on the radii of the beam; one by changing the voltage while holding the current constant, the other by keeping the voltage constant and changing the current.
In our experiment, we held the current along the coils constant at 1.35A while fluctuating the voltage on the electron gun from a max value of 250V to a minimum voltage of 146V. We observed that the radius of the electron beam increased with the more voltage we applied while keeping the current constant. In the next set of experiments, we kept the voltage constant at 143V and changed the range of current from 0.9A to 1.33A. We observed that the radii increased as we decreased the current along the coils. We took data on the radii versus the current and radii versus the voltage and this can be found on my data page for this lab.
Analysis Methods
The theory predicts that there is a relation between the magnetic field and the force at which electrons travel in an electromagnetic field. From this we can use the Boit-Savart Law1 (see Equation 1) to find the magnetic field. The Lorenz Force 4(see Equation 2) can be solved for to find the ratio of e/m by means of knowing the velocity (Equation 3). By knowing this, the theory will predict a linear relationship between the Radii and the velocity when current remains constant (Equation 4) with the ratio of m/e being the slope. The theory also predicts that there is also a liner relationship between the radii and the inverse current squared (Equation 5) where voltage remains constant. We used the Microsoft Excel function LINEST, to find this slope for both the constant current and constant voltage data. [math]\displaystyle{ Equation 1: B=\frac{\mu R^2NI}{\left(R^2+x^2 \right)^2} }[/math]
[math]\displaystyle{ Equation 2: \vec{F}=e(\vec{v} \times \vec{B}) = m \frac{\vec{v}^{2}}{R}=\frac{e}{m}=\frac{|\vec{v}|}{R|\vec{B}|} }[/math]
[math]\displaystyle{ Equation 3: v=\sqrt{\frac{2eV}{m}} }[/math]
[math]\displaystyle{ Equation 4: \frac{m}{e}\times V=\frac{(7.8\times10^{-4}\times I \times R)^2}{2} }[/math]
[math]\displaystyle{ Equation 5: \frac{m}{e}\times \frac{1}{I^2}=\frac{(7.8\times10 ^{-4}\times R)^2}{2\times V} }[/math]
A more detailed method for my calculations can be found here.
Results and Discussion
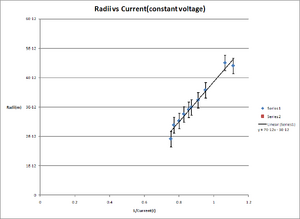
The data given in Table 1(Fig.4) shows the results that were obtained while keeping the voltage constant at 143 volts. The graph of radii vs 1/I^2, showing how the data compares to a best fit line (using Microsoft Excel,Fig. 5) shows that most of the data fulls within one standard deviation of the linear fit. The value of e/v was determined to be 2.74+/-0.38*10^11 coul/kg within 68% confidence interval, which has an error of approximately 55.76% when compared to the value from the paper "The Electronic Atomic Weight and e/m Ratio6" of 1.76*10^11 coul/kg.
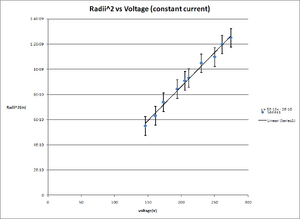
From Table 1(Fig. 4), the value of e/m while holding the current constant at 1.35 amps was 1.85+/-0.12*10^11 coul/kg. Using Microsoft Excel, a plot of our data radii62 vs voltage(Fig. 6) is compared to a liner fit of the data, and as there is no obvious systematic deviation this is a good fit for the data. From our value for e/m the error is 5.27% when compared to the value from "The Electronic Atomic Weight and e/m Ratio6" of 1.76*10^11 coul/kg.
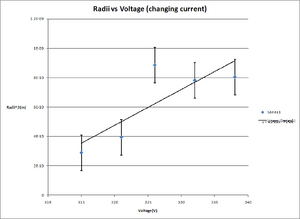
From Table 1(Fig. 4) the value of e/m was calculated while the voltage and current were both being varied. This value was 4.091+/- 0.82*10^11 coul/kg. The liner graph displays the varying values are radii^2 vs voltage(Fig. 7) shows again that even while the voltage and current are varied, a linear fit still holds. An error of 76.8% was found when compared to the value in "The Electronic Atomic Weight and e/m Ratio6" of 1.76*10^11 coul/kg. Therefore the data does not fit the linear approximation when the current and the voltage are not held constant. An even larger error is generated as compared to the accepted value of e/m.
Conclusion
So from our experiment to find the ratio for e/m, the result closest to the accepted value was obtained when we held the voltage constant and varied the current, resulting in a value of [math]\displaystyle{ 1.85\pm.12*10^{11}\frac{coul}{kg} }[/math].
SJK 16:20, 15 December 2009 (EST)

I think you're mixing systematic / random a bit here. For example, losing energy to helium would cause a systematic error (it can only lose energy, not gain).
So based on our calculations from the above section, the best results were obtained while taking the value using constant voltage, resulting in an error of approximately 5.11%. This is not a bad result considering that there is a significant amount of systematic and random errors present in this lab. The sources of random (non-biased) error in this lab are as follows. The collisions that occur between the helium atoms in the bulb and discharged electrons from the electron gun, some of the energy that is used to accelerate the electrons is wasted in the form of visible light due to the collisions so the energy that is measured is an overestimate. Some of the systematic errors are caused by the imprecision of the ruler and in aligning the ruler with the electron beam. We tried to overcome some of this by taking two readings -- one on the left side and one on the right -- and averaging the two. Our average only decreased the error but did not eliminate it completely. Another error happens when either the voltage is raised or the current is lowered and the discharge of the electron beam doesn't line up with where it impacts the electron gun. We adjusted for that effect by means of the focus knob, however, this changes the radii of the electron beam so we needed to adjust the focus every time we changed the voltage and/or current. A lack of adjustment can potentially alter the data and throw off the results.
The experiment showed me that an electron beam when in the presence of a uniform magnetic field creates a circular form. The radii of the circle is directly related to the strength of the magnetic field and the velocity at which the electrons leave the electron gun. If I were to do this experiment again I would not expect to obtain values so close to the actual value for e/m due to the potential of a large amount of systematic and random errors that can be introduced into the experiment. Fundamental constants can be found even with potentially large amounts of systematic and random errors.
Acknowledgments
I would like to thank my lab partner Elizabeth Allen, my lab professor Dr.Steven Koch, and our lab TA Pranav Rathi for their assistance and support in this lab. I would also like to thank my mother (Dixie Colvin) for her assistance in editing this paper thanks mom.
References
1.M. Gold, Physics 307L: Junior Laboratoy, UNM Physics ans Astronomy (2006),[1]
2. J. Thompson, "Cathode Rays". The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, Vol 44, 293-316 (1897).
3.R. A. Millikan, "On the elementary electrical charge and the Avogadro constant". The Physical Review, Series II 2: 109–143 (1913).
4.Darrigol, Olivier, "Electrodynamics from Ampère to Einstein",Oxford University Press, ISBN =0-198-50593-0, 327 (2000)[2]
5.R. Merritt, C. Purcell, and G. Stroink. "Uniform magnetic field produced by three, four, and five square coils". Review of scientific Instruments, Volume 54, Issue 7, 879 (1983).
6.R.C. Gibbs and R.C. Williams, "The Electronic Atomic Weight and e/m Ratio". The Physical Review, Volume 44, Issue 12, 1029 (1933).