User:David J Weiss/Notebook/notes E/m Ratio
E/M Ratio Notes
SJK 17:56, 15 November 2009 (EST)

Excellent primary lab notebook. Except for a little bit of the analysis it was very easy to follow.
In this lab we will be studying the effects of electric and magnetic fields on charged particles with mass, and studying the mass charge ratio of an electron (e/m).
Equipment
Digital Voltmeter BK Precision Model 2831B
Deluxe Regulated Power Supply Gelman Interment CO. Model 38520 115V
DC Power Supply Soar Corporation 7400 Series 117V
Hewlett Packard dc power supply model 6384A
e/m Experimental Apparatus Model TG-13 Uchida Yoko
Safety
The main safety concerns associated with this lab are:
- 1)Electrical die to the fact the you will use a dc power supply that will be 150-300V at 2A
- 2)Equipment Safety do not drop the e/m apparatus due to the fact that it is glass and that it will break and that it is pressurized
- 3)Don't cut your self if you were dumb enough to break the e/m apparatus glass is sharp
Set Up
From Dr Golds Lab Manual
Connect a regulated 6-9 Vdc supply rated at 2 A to the Helmholtz coil jacks. Be sure to observe the color-coded polarity on all input jacks. You will need to connect an ammeter in series between the supply and the coil jacks so that you can measure the current to 1% or better accuracy. A wire wound potentiometer control to the right of the coil jacks on the panel serves to adjust the current in the coils. Now connect a 6.3 V (ac or dc, but do not exceed 6.3 V!) supply rated at 1.5 A to the heater jacks of the electron gun at the right side of the base panel. Besides powering the heating element, this supply also powers the small scale lamps on the coil brackets. Lastly connect a high voltage source of 150-300 Vdc rated at 40 mA to the Electrode jacks of the electron gun. The high voltage applied to the anode of the gun accelerates the electrons boiled off from the cathode to form the necessary electron beam. The value of this voltage determines the average velocity of the electrons in the beam and appears in the final expression for the ratio of e/m. Regardless of the metering on your high voltage supply, the accelerating voltage must be measured with an accurate dc voltmeter connected at the jacks labeled Voltmeter on the base panel.Turn the Current Adjust control to zero and set the switch on the panel to the e/m position. Nothing should be connected to the jacks labeled Deflection Plates at this time. Turn on the Heater supply and allow the electron gun filament to heat up for two minutes. At the end of this time apply a 200 Vdc potential from the high voltage supply to the Electrodes for the initial value of accelerating voltage. With the accelerating voltage on, you should be able to see the violet hue of the electron beam projecting horizontally from the electron gun. For proper viewing of the beam this experiment should be conducted in a darkened room or in subdued lighting using a black cloth hood to mask the tube and to backdrop the beam. Turn on the coil current and increase the Current Adjust control from zero to a current value that bends the beam around into a complete circle on itself. It may be necessary to rotate the tube socket until the end of the curving beam strikes between the two wire leads supplying the heating filament on the left side of the electron gun. This brings the beam and gun into an exact parallel position with the plane of the coils.
Notes
Day 1
- Worked with Elizabeth Allen
- Went through a safety brief with Dr Koch.
- Connected the various cables to their respective ports and let the heater warm up for two minutes.
- Turned on the power supply on the electron gun and set the voltage to 200V
- Having trouble seeing the purple hue of the electron beam adjusting the voltage of the power supply.
- Switched out the power supplies for the heater with the power supply on the Helmholtz coil and letting the electron gun warm up again at 6.3V
- Turned on the electron gun at 200V and saw the purple hue with no problems increased the voltage to 7V on the heater
- Turned on the Helmholtz coil to bend the electron beam around in a circle to do this we have to adjust the current adjust knob on the e/m apparatus
- Got the electron beam to go around in a circle. Adjusting the voltage on the electron gun will decrease the size of the circle (IE its radius) the smaller the voltage the smaller the radii and the larger the voltage the larger the radii. Adjusted the bulb to get the circle of the electron beam centered on the zero mark of the ruler on the back of the e/m gizmo.
- Found out that we can not take readings of the current when the devices are parallel they have to be in series.
- Took readings of radii of the electron ring and current required to bend the electron beam and the voltage to create the electron ring from the electron gun.
- To get the readings for the radii you have to look at the ruler and find the reflection of the electron beam then line it up with the actual electron bream witch is kind of a pain in the ass but whats new.
- We did this number of different 5 times while varying the voltage and current and getting different radii for each change
Day 2
- worked with Elizabeth Allen again
- Replaced the bulb on the e/m experimental apparatus
- Set up the equipment and let the heater warm up
- New bulb seems to give a better image of the electron beam and we found a new feature on the e/m apparatus which is the focus knob which I think is used to create a narrower path for witch the electrons will travel
- We started the experiment with a constant current of 1.35A and varied the voltage to see how the radii change we took 10 readings of data this way
- We then set the voltage constant at 143V and adjusted the current to get different radii and took 10 readings this way
- when we hit the values of .9A and 143V the electron beam starts to change its shape on the left side for reasons that i cannot explain at this time
- Took 10 readings while varying the voltage and current and took 10 readings for the radii
- We then took new sets of data for the readings 143V and 1.1A to try to find the SEM for the radii and for 183v and 1.09A
Data
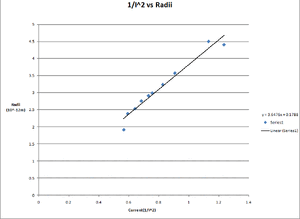
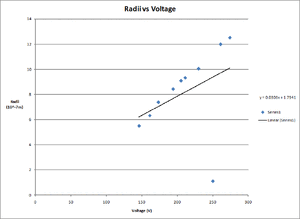
SJK 16:52, 15 November 2009 (EST)

It looks like you forced the fit to go through the origin, causing the fit to be very poor. Do you think this is the best idea? Or have any ideas how to deal with this problem?
Calculations
- The calculations for the magnetic field can be given by [math]\displaystyle{ B=\frac{\mu R^2NI}{(R^2+x^2)^{\frac{3}{2}}} }[/math] which simplifies down to [math]\displaystyle{ B=\frac{7.8*10^{-4}I}{web*A*m^2} }[/math] which olny depends on the current (I).
- After you know the current you can find the ratio of e/m. This comes from the Lorenz Force [math]\displaystyle{ \vec{F}=e(\vec{v}\times \vec{B})=m\frac{\vec{v}^2}{R} }[/math] which implies [math]\displaystyle{ \frac{e}{m}=\frac{\left|\vec{v} \right|}{R\left|\vec{b} \right|} }[/math] and because the electrons are accelerated through a potential [math]\displaystyle{ \frac{1}{2}mv^2=eV }[/math] solving for v gives [math]\displaystyle{ \sqrt{\frac{2eV}{m}} }[/math]. Then substituting in for e/m gives [math]\displaystyle{ \frac{e}{m}=\frac{2V}{(RB)^2} }[/math] so now we can find the value of e/m by knowing the voltage(V) that was applied the current(I) that was used and the radius(R) that the electron beam generated.
- The final equation for constant current can be rewritten as [math]\displaystyle{ \frac{m}{e}\times V=\frac{(7.8\times10^{-4}\times I \times R)^2}{2} }[/math] with radii and voltage being the unknowns when you have a constant current and the ratio of m/e is the slope.
- The final equation for constant voltage can be written as [math]\displaystyle{ \frac{m}{e}\times \frac{1}{I^2}=\frac{(7.8\times10 ^{-4}\times R)^2}{2\times V} }[/math] with voltage being a constant and the radii changing and the current changing
I found these on other Junior Lab Persons pages thanks Bolestaw L. Osinki.
Used the excel function linest to find the slope and the standard error for the graphs above for the e/m ratio. I found the slope for m/e and I then had to take the inverse to find the slope for e/m and i then took that to get the average value for it by taking the value for the first with constant voltage and then taking it for constant current and added them together and divided by 2 to get the average. For the standard deviation I took the values for the slope I found and added them and subtracted them from the average and then converted to the slope for e/m by taking the inverse and then subtracted the value out of the value i got for the e/m value. I did this for both constant current and constant voltage and then added them and divided by 2 to get an average value for the standard deviation.SJK 17:50, 15 November 2009 (EST)

I can almost follow your method here, and it appears that you're developing a method for error propagation and weighted means. I think (but am not sure because it's tough to follow) that your method for propagating error from slope to e/m was correct. However, your method for weighted mean is not correct. I think subsequent to you turning in this lab, we learned how to do a weighted mean, along with calculating the new uncertainty in class. It's not a simple averaging of the uncertainties. In fact, your new uncertainty will be less than your smallest uncertainty. Finally, you should ask your question: does it make sense to average these two values? Do they really represent the same parent mean? Or are they likely statistically significantly different? We discussed this in class too.
For the constant current (I) the slope was 1.8528*10^11 coul/kg and the standard error was .1179*10^11 coul/kg. For constant voltage (V) the slope was 2.741*10^11 coul/Kg and the standard error was .3593*10^-11 coul/kg.
So my average value for [math]\displaystyle{ \frac{e}{m}=2.3(\pm .23)\times 10^{11}\frac{coul}{kg} }[/math]
Taking the accepted value from Dr Golds Lab Manual of 1.76*10^11 coul/kg so using the formula [math]\displaystyle{ \frac{Expernmental-Accepted}{Accepted}= % Error }[/math][math]\displaystyle{ =\frac{2.3\times 10^{11}\frac{coul}{kg}-1.76\times 10^{11}\frac{coul}{kg}}{1.76\times10^{11}\frac{coul}{kg}}=30.68% }[/math]
Error
- The errors that come up in this lab are that of reading the radii from the ruler on the back of the electron gun. One way to reduce the error is to take a measurement from the right and then one from the left and calculate the average of the two and taking the this for all the values of the radii to get a precise reading for the radii. This is an example of a systematic error and we can only do so much to correct this due to the fact that this measurement was done with the naked eye and is only an approximation so we do the best we can.
- Another source of error could come from the multimeter and depending on how precise the readings that are given could tell you how far the error was in determining the voltage and the current seeing that the multimeter was connected to both the current generator and the voltage generator. This is another example of systematic error in that every reading on the multimeter will have the same amount of systematic error and thus the reading are approximately off by a standard amount so the data works in this case.
SJK 17:52, 15 November 2009 (EST)

Check out Elizabeth's writeup for many more ideas about systematic errors in this lab.
Questions
1. Why do we see the electron beam at all?
- The reason we see the electron beam at all is that the excited electrons are in constant collisions with the gas in the electron gun bulb which are exciting the electrons and causing an emitted light to be viewed when the gas goes back to its unexcited state, in the form of an electron beam. then the collisions are bent in terms of making the electrons travel in a certain path. So the collisions are along that certain path so that is why you see the electron beam when you apply the current to the Helmholtz Coil creating the path that the electrons travel.
2. We ignored the Earth’s magnetic field in our procedure. How much error does this introduce into this experiment? (see http://www.ngdc.noaa.gov/seg/geomag/)
- The magnetic field for this location from the (NOAA Geophysical Data Center online calculator http://www.ngdc.noaa.gov/geomagmodels/struts/igrfWmmZip;jsessionid=747B806039AF0A00BD652BBB3A576B02) is 49786.8 nano-Tesla taking this into account the magnetic field would no really change in terms of the field being 1.053*10^-3 Tesla and the field at this altitude being 4.79868*10^-5 Tesla so the effect is minuscule so that introduces very little error in the experiment.
3. Suppose that protons were emitted in the vacuum tube instead of electrons. How would this effect the experiment?
- If protons were emitted in the experiment the results for the ratio for e/m would be lower due to the fact that the proton has a larger mass approximately 1.762*10^3 times bigger than that of the electron so the charge to mass ratio would be 1.762 times smaller for a proton rather than an electron.