User:Alex G. Benedict/Notebook/Physics 307L: Junior Lab/e over m Lab
Steve Koch 04:14, 21 December 2010 (EST):Good primary lab notebook.
e/m Lab
This lab was performed in the junior laboratory in the UNM physics building on October 11, and October 18 with Joseph Frye.
Pictures courtesy of Joseph Frye.
Links
Equipment and Setup
- 3 Power supplies
- Gelman Deluxe Regulated Power Supply, 6-9V 2A
- Soar DC Power Supply model PS 3630, 6.0V 1.5A
- Hewlett Packard 6236B, 150-300V 40mA
- 3 Digital Multimeters
- e/m Experimental Apparatus Uchida model TG-13
Procedure and Data
We followed the procedure in the lab manual linked above. Everything was already assembled so we just took measurements as the lab manual suggested, we took 22 measurements, 11 at constant voltage and 11 at constant current. The second week was spent investigating the behavior of the beam in the low voltage, high current limit.
Download the spreadsheet below, not an image:
Results
As can be seen in the spreadsheet above, the value for the e/m ratio obtained by direct calculation was 217349888422.149 +/- 1940461666.18754. Which has a relative error of 0.23577095674397. Which is pretty high, and so we were going to take more measurements to improve the data, but our fractional error, the mean over the SEM was 0.008927824533402 which is very low. So the model used to analyze the data must be flawed. So there must be something not being accounted for in the model. A source of systematic error was suggested as being the Earth's magnetic field. But if we take the observed value of e/m was a function of voltage and the B field, and expand it in a taylor series about both variables a much larger error would arise from a change in voltage than in the magnetic field. But the voltage is really being used in the simple equation as a simple model for the kinetic energy of the electrons, and it is assumed that the electrons would be moving in a vacuum. But as they move through the loop they lose energy to the helium gas in the tube. Since they are losing kinetic energy, we can model it as them moving in a field with a retarding potential. And their loss of kinetic energy should be proportional to the length of their path through the gas. So we introduce a parameter d and we take the retarding potential to be d*R where R is the radius of curvature. And then we can just subtract the retarding potential from the accelerating voltage to get the net voltage. Using that model and with d=1085.714 we had an average e/m of 177021197987.078 +/- 2285072583.70116 and a relative error of 0.006476961127175.
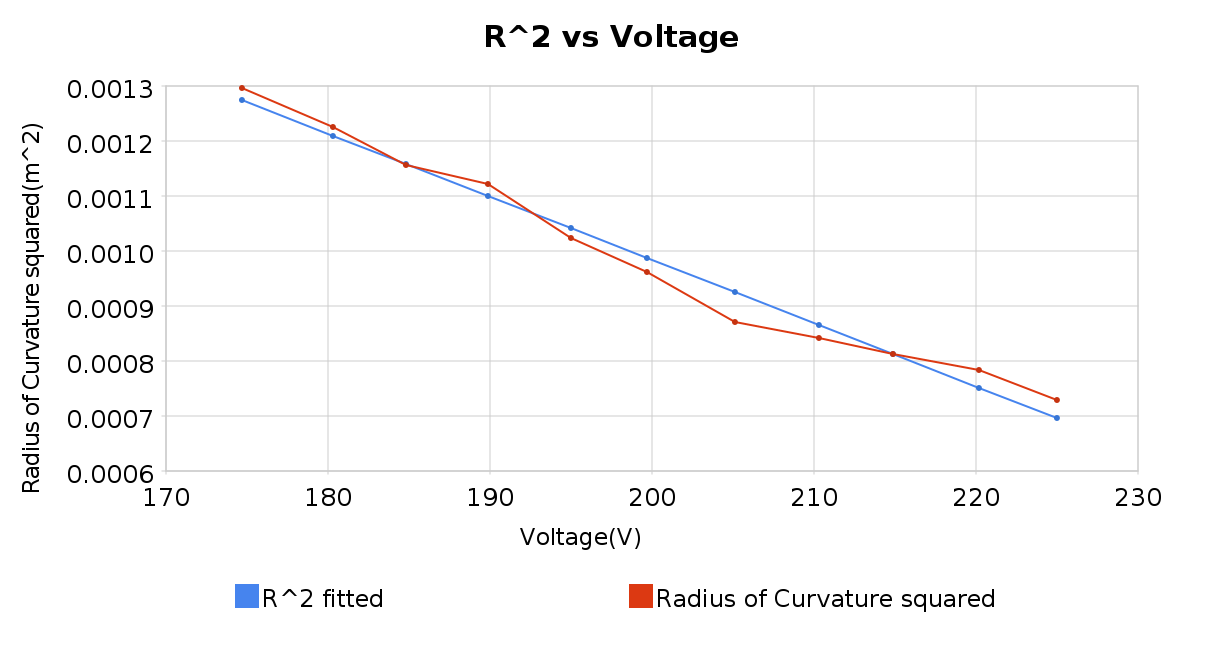
Gold suggested performing two least squares fits one of R vs. B^-1, and one of R^2 vs V. The results are in the spreadsheet above, and have 68% confidence intervals of [204691017245.544,237221836807.536] and [121206094246.381, 133676161824.731]. Since they are both horrible results, but on opposite sides of the accepted value, I took an unreasonable average of the two and got a value with a relative error of 0.012992677653958. or about 1%. The lines are plotted below along with the best fit line for each.