The Benefits of Small Length Scales in Microscale Systems - Telvin Abariga
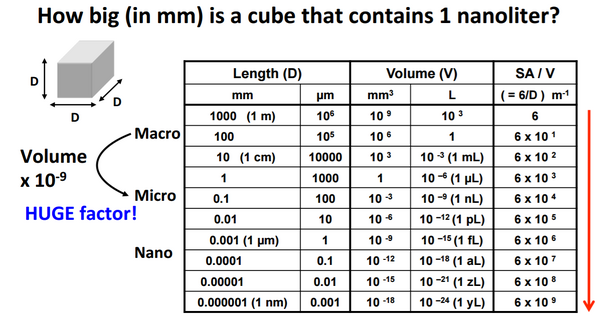
Microfluidics is a technology that pertains to the manipulation of flows at the microscale. The fluid phenomena that govern flows at the macroscale differ greatly from those that govern fluid flow at the microscale, and these impact the heat and mass transfer in different ways. Microfluidics takes advantage of the scaling law, which describes how physical quantities vary as a function of the system size as shown in figure 1. For example, the area of an object scales with the square of its length whereas the volume of an object scales with the cube of its length. [1]
There are a variety of benefits involved with transitioning from the macro scale to the microscale. Chief amongst them are the fact that there is less material consumption, along with greater portability and safety. An additional value of transitioning to the microscale is the opportunity to explore new reaction pathways and find environmentally friendly methods to produce chemicals.
Scientific Background
Gravity, like surface tension, is a force that tends to influence fluids. Since gravity’s effects are generally related to size, its effects diminish at the microscale. Surface tension plays a more dominant role at the microscale and this phenomena can be exploited to direct flow in channels. Furthermore, the diminished effect of gravitational forces at the microscale means that fluid flow is governed by capillary action. The small volume limits the amount of mass in the system, which under the right conditions, is much easier to move. Also, as the volume decreases, the surface area to volume ratio increases drastically. Because heat transfer happens across the surface area, a greater surface area allows a much greater heat gain or loss throughout the entire system. As proven mathematically, the rates of heat and mass transfer increase drastically as the length scale decreases to the point that even very slight changes in length lead to big changes in rate. Due to this large change in heat and mass transfer over small changes in length, very sharp heat and mass gradients form within microscale systems. There are numerous applications for these different gradients in research and industry based processes.
Laminar Flow
Flow in microfluidic systems experience minimal mixing due to the lack of turbulence when working on the micro-scale. The Reynolds number, a dimensionless number that describes the flow regime of the system by relating inertial and viscous forces, is given by:
- [math]\displaystyle{ \mathrm{Re} = \frac{Inertial}{Viscous} = \frac{\rho v L}{\mu} }[/math]
where:
- [math]\displaystyle{ \rho }[/math] is the density of the fluid (kg/m^3)
- [math]\displaystyle{ v }[/math] is the velocity of the fluid (m/s)
- [math]\displaystyle{ L }[/math] is the characteristic length of the channel, which varies for circular pipes, square ducts, and other geometric channels (m)
- [math]\displaystyle{ \mu }[/math] is the dynamic viscosity of the fluid (Pa*s)
Given that the Reynolds number is directly proportional to the characteristic length (L) of the channel, flow in microscale channels often falls under the laminar flow regime as the Reynolds number does not come close to approaching the transition point for turbulent flow, which occurs at around 2300. A macro example of laminar flow is shown in figure 2. In addition, the effects of inertia become minimal as inertia is dependent on mass, which becomes insignificant on the microscale. [2] The significance of viscous effects over the inertial effects of the flow produce very little mixing. Under two-dimensional laminar flow, neighboring streamlines form a distinct boundary where diffusion occurs. This characteristic property of microfluidic channels allows for controlled diffusion rates that can be tailored to specific chemical reactions and other applications. At the same time, the slow nature of passive diffusion, depending on the diffusion coefficient, calls for active mixing methods that require either physical or chemical means.
Mass Transfer
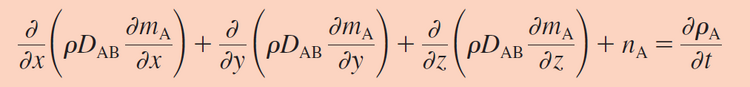
Equation 1. This is the most general form of Fick's First law in three dimensions for mass flux. In this equation, Dab is the binary diffusion coefficient which is an intrinsic property of the mixture of two components (m2/s), [math]\displaystyle{ \rho }[/math]o is the material density (kg/m3), Ma is the mass of a, and Na is equal to the rate of increase of species a. This is all equal to the rate at which the mass concentration of a with respect to time) -
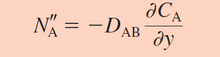
Equation 2. This is the simplified version of Fick's law for one dimension and steady state. This also has been converted into molar concentrations while the one above has been used for mass.
Fick's first law relates the concentration of a solute species to the diffusion flux of that species. This law states that the flux will move along a concentration gradient, from an area of high solute concentration towards one with a lower solute concentration. This concentration gradient is mathematically calculated as the partial derivative of solute concentration with respect to distance. Since distance is once again in the denominator of the governing transfer equation, working on the micro scale compared to the macro scale improves the transfer of mass exponentially. This gradient term is then multiplied by the diffusion coefficient which is specific for each system and conditions.
The mass transport in microreactors is generally dominated by viscous dissipation, and the inertial forces are generally negligible. Since inertia accounts for most of the irregularities in flow, the near absence of this inertia makes the flow in microchannels predominantly laminar. In microreactors, mass is propagated by diffusion, which is governed by Fick’s Law. [3] Fick’s Law is similar to Fourier’s Law in that it governs the rate of diffusion due to the concentration as shown in figure 3. Just as a temperature gradient constitutes the driving potential for heat transfer, the concentration gradient provides the driving potential for the transport of materials from a region of high concentration to a region of lower concentration. Another similarity between Fourier’s Law and Fick’s Law is that the rate of transfer is inversely proportional to the length, therefore, the short distance of microreactors creates sharp diffusion gradients which allows for a shorter diffusion time and also reduces the possibility of side reactions occurring by limiting the residence time in the microreactor.
Heat Transfer
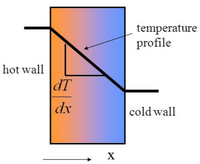
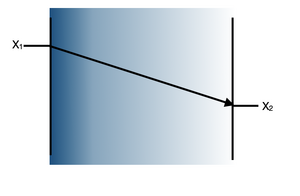
The primary mode of heat transfer in microreactors is conduction. Conduction is the transport of energy in a medium due to a temperature gradient from the hotter region to the cooler region. The physical mechanism is one of random atomic or molecular activity. [3] The small sizes of the channel reduces the resistance to heat. Conduction is governed by Fourier’s law and the use of the law to determine the heat flux depends on knowledge of the temperature distribution in the system. The law relates the rate of the heat transfer to its thermal conductivity coefficient, k. Figure 4 shows the Fourier’s Law and depicts how the law works. Here, T1 is at a higher temperature than T2 therefore heat is transferred from T1 to T2. The law essentially demonstrates that there is an inverse relationship between the rate of heat transfer and the distance. One of the primary reasons why reactions in microreactors have better yields and selectivity rates is because the miniature size of the reactor greatly improves heat transfer and allows for better heat control. [4] Microreactors tend to have surface area-to-volume ratios exceeding 20,000 m2/m3 which is significantly larger than the 1,000 m2/m3 surface area-to-volume ratio conventional reactors tend to have. Furthermore, alternative reaction pathways which may seem impossible to execute in conventional reactors may be carried out in microreactor due to the the aforementioned characteristics.
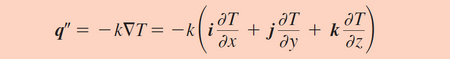
Applications
Mass Transfer
Working on the microscale not only improves the rate of mass transfer across the system it also allows the experimenter to finely tune the experiment by manipulating the concentration gradients. By exploiting the laminar flow in microfluidic systems, it is possible to achieve separation without the use of an adsorbent or separating agent. An example of this is the separation of waste urea from blood without the use of a membrane. The only way that this could even be possible is using a glomerulus microchannel, where the laminar flow profile prevents mixing between the blood and a solution of albumin, urea, and glucose. The large molecule of albumin has difficulty traveling through the two fluids, creating a concentration gradient. This allows almost all of the small molecules within the blood, especially urea, to travel very effectively over a short distance from the blood to the albumin mixture. [5] Another application of a short mass transfer gradient in microfluidics is in protein crystallization and the use of counter diffusion (diffusion of two different species from opposite directions to come into contact) between the protein and precipitants. The only way to fine tune the gradients of both the protein and precipitate (which helps enable the crystallization of the protein to a certain extent) through mass diffusion, without convective mixing and this is only possible at the microscale.
Microfluidics has also been applied to the study and analysis of human organs, particularly, human lungs and liver. A microfluidic device has been designed to study how the toxicity from external stimuli can affect the lungs. In the device, two channels were separated by a porous flexible membrane coated with ECM. Human alveolar epithelial cells were grown on one side of the membrane, and human pulmonary microvascular endothelial cells were grown on the other side. Microfluidic technology made it possible to observe and analyze the transport of nanoparticles across the porous membrane. The result was a transfer of particles across the membrane by a factor of four which is a further testament to the rate of transfer in microfluidic devices.
Heat Transfer
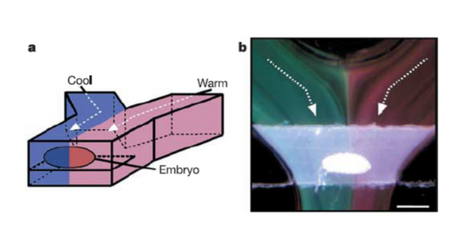
Due to the laminar flow of fluids at the microscale, it can be tricky to achieve mixing in microfluidic devices; however, it makes for easier separation. It is possible to have a hot stream and a cold one exist right next to each other without having a huge temperature gradient, due to the very small distance in between them. For example, a hot temperature and a cold temperature stream can be simultaneously applied to either side of a fruit fly embryo, as shown in Figure 5. [6] Another application for the sharp temperature gradient of microsystems is the vitrification of protein crystals through cryo-cooling. In order to solidify protein crystals without deforming their structure in ice, it is necessary to essentially super-freeze water past the state of ice and into a glass-like state. To do this, the protein crystal in solution must be supercooled instantaneously and the only way to cool something that fast is with the incredibly high rate of heat loss that is characteristic in microscale systems.
References
- Sun, B.; Jiang, J.; Shi, N.; Xu, W. Application of Microfluidics Technology in Chemical Engineering for Enhanced Safety. Process Saf. Prog. 2015, 35 (4), 365–373. https://doi.org/10.1002/prs.11801.
- Squires, T. M.; Quake, S. R. Microfluidics: Fluid Physics at the Nanoliter Scale. Rev. Mod. Phys. 2005, 77 (3), 977–1026. https://doi.org/10.1103/RevModPhys.77.977.
- Bergman, T. L.; Lavine, A. S.; Incropera, F. P.; DeWitt, D. P. Fundamentals of Heat and Mass Transfer, 7th Edition; John Wiley & Sons: Chichester, England, 2011.
- Chambers, R. D.; Spink, R. C. H. Microreactors for Elemental Fluorine. Chem. Commun. (Camb.) 1999, No. 10, 883–884. https://doi.org/10.1039/a901473j.
- Garman, E. Cool Data: Quantity AND Quality. Acta Crystallogr. D Biol. Crystallogr. 1999, 55 (10), 1641–1653. https://doi.org/10.1107/s0907444999008653.
- Lucchetta, E. M.; Lee, J. H.; Fu, L. A.; Patel, N. H.; Ismagilov, R. F. Dynamics of Drosophila Embryonic Patterning Network Perturbed in Space and Time Using Microfluidics. Nature 2005, 434 (7037), 1134–1138. https://doi.org/10.1038/nature03509.
