Péclet number (Pe) - Nishanth Saldanha

Definition

The Péclet number (Pe) is a dimensionless number that represents the ratio of the convection rate over the diffusion rate in the a convection-diffusion transport system. ^[1][2]

[math]\displaystyle{ Pe = \frac{(Convection \, rate)}{(Diffusion \, rate)} = \frac {UL}{D} }[/math] U represents linear flow in a control volume, L represents the length scale of the flow and D is the diffusion constant.

This number can also be represented as a ratio of diffusive to convective time scales.

[math]\displaystyle{ Pe = \frac{(Diffusion \, timescale)}{(Convection \, timescale)} }[/math]

In diffusion dominated regimes, the Peclet number is less than zero. Such is the case with microfluidic systems, where turbulence is low. In convection dominated systems, this number is greater than one.

Derivation

For system as described in Figure 1, with a specie concentration, [math]\displaystyle{ C }[/math] following relations can be made to relate flux in, [math]\displaystyle{ J_{in} }[/math] , flux out,[math]\displaystyle{ J_{out} }[/math] and control volume [math]\displaystyle{ V }[/math]

Figure 1 This is an illustration of a control volume with fluxes in and fluxes out. If sources and sinks can be neglected, these fluxes can be contributed to convection and diffusion

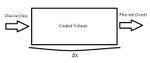
[math]\displaystyle{ V\frac{dC}{dt} = A\cdot J_{in} - A\cdot J_{out} }[/math]

[math]\displaystyle{ \frac{dC}{dt} = \frac{A}{V}\cdot (J_{in} - J_{out}) }[/math]

[math]\displaystyle{ J_{out} = \frac{\partial J}{\partial x}\cdot (\Delta x)+J_{in} }[/math]

[math]\displaystyle{ \frac{dC}{dt} = \frac{A}{V}\cdot \frac{\partial J}{\partial x}\cdot (\Delta x) }[/math]

[math]\displaystyle{ \frac{A}{V} = \frac{1}{\Delta x} }[/math] [math]\displaystyle{ \frac{dC}{dt} = \frac{\partial J}{\partial x}\rightarrow \frac{\partial C}{\partial t} =\triangledown J }[/math]

[math]\displaystyle{ J = J_{convection}+J_{diffusion} }[/math]

[math]\displaystyle{ Convection }[/math] [math]\displaystyle{ Q = C \Delta x\cdot A }[/math]

[math]\displaystyle{ J_{convection} = \frac{Q}{\Delta t\cdot A} = \frac{C \Delta x }{\Delta t} \rightarrow \frac{\partial x}{\partial t}C }[/math]

[math]\displaystyle{ Diffusion }[/math]

[math]\displaystyle{ J_{diffusion} = -D \frac{\partial C }{\partial x} }[/math]

[math]\displaystyle{ \frac{\partial C}{\partial t} = -\frac{\partial \left [ J_{convection}+J_{diffusion} \right ]}{\partial x} = -\frac{\partial \left [ \frac{\partial x}{\partial t}C + -D \frac{\partial C }{\partial x} \right ]}{\partial x} }[/math]

[math]\displaystyle{ \frac{\partial x}{\partial t} = u }[/math]

[math]\displaystyle{ \frac{\partial C}{\partial t} = D\frac{\partial^{2} C}{\partial x^{2}} - u \frac{\partial C}{\partial x}\rightarrow \frac{\partial C}{\partial t} + u \frac{\partial C}{\partial x}= D\frac{\partial^{2} C}{\partial x^{2}} \rightarrow \frac{\partial C}{\partial t} + u \triangledown C= D \triangledown^{2} C }[/math]

[math]\displaystyle{ C^{*} = \frac {C}{C_{max}}; U^{*} = \frac{u}{U}; t^{*} = \frac {t}{t_{0}} }[/math]

[math]\displaystyle{ \frac{C}{t_{0}}\frac{\partial C^{*}}{\partial t} + \frac{UC}{L}u^{*} \frac{\partial C}{\partial x}= \frac{DC}{L^{2}}\frac{\partial^{2} C}{\partial x^{2}} }[/math]

[math]\displaystyle{ \frac{L^{2}}{D\cdot t_{0}}\frac{\partial C^{*}}{\partial t} + \frac{UL}{D}u^{*} \frac{\partial C}{\partial x}= \frac{\partial^{2} C}{\partial x^{2}} }[/math]

[math]\displaystyle{ Pe = \frac {UL}{D} }[/math]

References

[[1]] "Advection and diffusion of an instantaneous release". Heidi Nepf. 1.061 Transport Processes in the Environment. Fall 2008. Massachusetts Institute of Technology: MIT OpenCourseWare, License: Creative Commons BY-NC-SA.

[[2]] Incropera, F., DeWitt, D., Bergman, T., Lavine, A. Fundamentals of Heat and Mass Transfer”; Wiley: New York. 2011

[[3]] "Derivation of basic transport equation". Ali Ertürk. Lagoon Ecosystem Modelling (ECOPATH/ECOSIM): From Hydrodynamics to Fisheries. June 21- 23, 2011, University of Klaipeda and Leibniz Institute for Baltic Sea Research Warnemünde