Sebastian Poisson Statistics
Steve Koch 22:00, 21 December 2010 (EST):This lab, you could have benefited from an iteration, and upping the PMT voltage to recommended level, in order to get more counts in reasonable time frame.
Partner
Purpose
- The purpose of this lab was to explore and understand the properties of a Poisson Distribution by observing/recording the background radiation in the lab. The events (radiations or counts) should occur randomly and independently, but have an average value. We used an scintillator-PMT device to detect the background radiation and the computer software (UCS 30 Software) to keep track of the radiations or counts.
- The probability for a Poisson distribution is given by:
"[math]\displaystyle{ P_\mu (\nu) = e^{-\mu} \frac {\mu^{\nu}} {\nu !} }[/math]
Where:
- P is the probability of ν counts in any definite interval,
- μ is the expected mean number of counts, and
- ν is the number of counts in the interval." - taken from Brian Josey's Lab Summary for Poisson Distribution.
Lab Data
My Lab Notebook
Poisson Statistics - November 10, 2010
Equipment
- Combined Scintillator and PMT
- Computer running UCS 30 software
- Lead Bricks
- Spectech Universal Computer Spectrometer Power Supply
Lab Summary
My partner and I used our time in the lab simply collecting data. This consisted of turning on the power supply that supplied the scintillator-PMT, and then starting the software that recorded the radiation. We did not have to set any of the equipment up, but we did have to do some minor setting up in the software. More about this setup can be found in my primary lab notebook. We were basically recording the number of counts or radiations in a specified amount of time. Each specified time was divided into 256 equal "bins." So for our 10ms trial, each of the 256 bins had a time width of 10ms. The most complicated part of this lab was the data analysis. We had to save the files that contained our counts for each bin as a .csv file. After doing some research on the second day of lab, I found out that Google Docs could import these types of files. I imported each set of data and analyzed it as shown in my lab notebook.
Calculations and Results
As specified in the lab manual, Prof. Gold's Lab Manual, I calculated the standard deviation for each set of data (meaning the standard deviation of the counts column in the raw data that can be found in my primary lab notebook). Because we are analyzing experimental results, we would expect something that is not a true Poisson Distribution. A true distribution should have a standard deviation that is equal to square root of the mean of the data. So we also calculated the mean, and then the square root of the mean. Finally, the % error between these two values is reported.
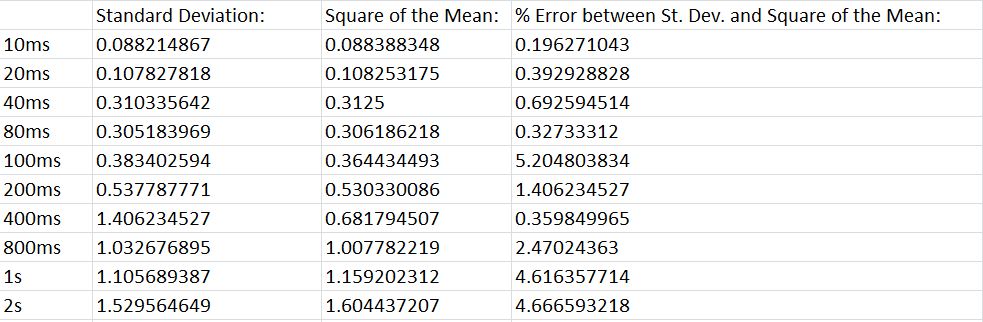
This graph summarizes the results for a few time intervals. All the time intervals can be seen in my primary lab notebook.
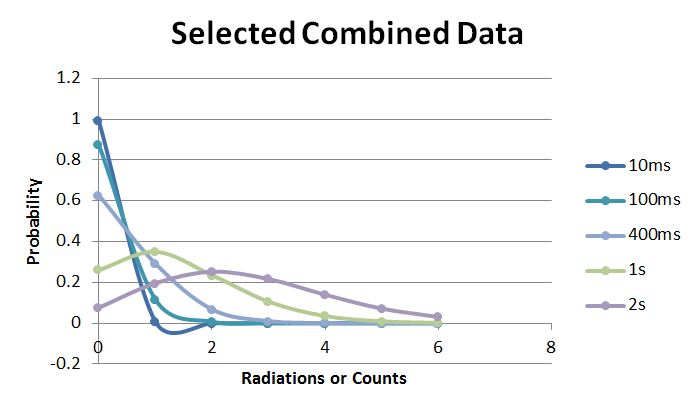
- From the table, we can see that the square root of the mean is always pretty close to the standard deviation. This is what we would expect though because it is a fundamental property of the Poisson Distribution. I am not sure why our percent error rises as the dwell time increases. After checking other groups data, I saw that they had lower percent errors, but a much higher number of bins. So, if we would have collected more data, I would expect our percent error to decrease somewhat.
- Note: One of the curves dips below the horizontal axis and this should not be the case. The data does not ever go negative so I think it was an error on the computer's part. (Steve Koch 21:56, 21 December 2010 (EST):Yes, definitely not possible to have negative probability here. Probably you used a spline fit or something like that.)
