Physics307L F08:People/Mondragon
This is my page for Junior Lab, Fall 2007. Links to my notebook and my main OWW page, where you can find contact info, below
[http://www-hep.phys.unm.edu/~gold/phys307L/manual.pdf Quick link to lab manual here]
The Poisson fit accuracy tests
Oscilloscope Lab Summary
Main notebook entry here.
see comment

To get practice in using an oscilloscope, I adjusted the volts/div, time/div, and trigger settings on the oscilloscope to get the oscilloscope to display a ~200Hz sine wave, triangle wave, and square wave. Adjusting the time and voltage settings improved how well the wave form were displayed on screen, and adjusting the trigger appropriately made the waveform displayed on the screen steady.
To gain experience taking measurements with an oscilloscope, I measured the amplitudes of these waveforms using the grid on the scope's display, the scope's horizontal cursors, and the scope's peak-to-peak measurement function. I then used the scope's vertical cursors to measure the scope's characteristic AC coupling fall time. The voltage the oscilloscope measured under AC coupling after a DC voltage step up declined to 10% after about 32ms meaning the characteristic fall time was about 14ms
e/m ratio summary
This experiment worked better than I initially expected. I haven't done any proper number crunching yet, but the e/m ratio that Lorenzo and I measured seems to float around [math]\displaystyle{ 2.9\pm0.2\times 10^{11} \tfrac{\mbox{coulombs}}{\mbox{kilogram}} }[/math]
Further investigation can be done in how electrons lose energy to the helium in the bulb and how this effects radius.
Poisson Statistics summary
SJK 01:46, 22 October 2007 (CDT)

Outstanding work, Tomas! Your work in getting the experiment working was a huge help, and the care and time you spent on data analysis are very evident. Also, I am intrigued about the weird 27 count event you saw. If you have a chance, get together with Nik and Bradley to see how their multi-day experiment turned out.
notebook entries Physics307L F08:People/Mondragon/Notebook/070926 and Physics307L F08:People/Mondragon/Notebook/071003
Poisson distributions model count data of an experiment that count events during a dwell time that happen at random but do so at a definite average rate. (Nuclear decay, photon detection, etc.) Lorenzo Trujillo and I set up some gamma ray detection equipment inside of a lead shielded cavity and counted the events the equipment detected in 256 10ms, 20ms, 40ms, 80ms, 100ms, 200ms, 400ms, 800ms, 1s, and 10s time intervals. The data we collected fit Poisson distributions very well, and the average count numbers fit on a line on a average count number versus dwell time very well just like anything following a Poisson distribution should. We were counting, on average, 7.39 events per second. There was an interesting instance were we counted 27 events in a 200ms period, though. I wonder what caused that. Could it be some weird particle creation and annihilation event?
Planck's Constant
Physics307L F08:People/Mondragon/Notebook/071010 Physics307L F08:People/Mondragon/Notebook/071017
We calculated [math]\displaystyle{ h=3.77989*10^{-15}\pm 0.14521*10^{-15} \,eV*s }[/math] based on data collected from our experiment that took advantage of the photoelectric effect and the emmision spectrum of mercury vapor. The accepted value of [math]\displaystyle{ h =\,\,\, 6.626\ 068\ 96(33) \times 10^{-34}\ \mbox{J}\cdot\mbox{s} \,\,\, = \,\,\, 4.135\ 667\ 33(10) \times10^{-15}\ \mbox{eV}\cdot\mbox{s} }[/math] is within three standard deviations of my calculated value. Looks like a systematic error.
Speed of Light
Physics307L F08:People/Mondragon/Notebook/071024 Physics307L F08:People/Mondragon/Notebook/071031
Excitation Levels of Neon
Physics307L F08:People/Mondragon/Notebook/071107 Physics307L F08:People/Mondragon/Notebook/071114
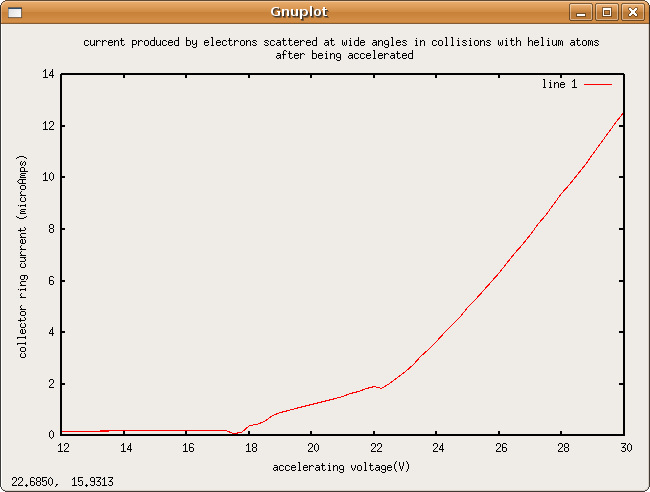
Not much usefull data was gathered, probably the wiring was wrong.
I think this may be a graph of whats supposed to happen with reversed collector ring bias, bot its flipped around an only shows some nubs. No peaks.
Our resolution was 0.25 V. No peaks found.
Rydberg constant/Balmer Series summary
Notebook entry here
The Balmer series is a sequence of lines in hydrogen's absorption/emission spectrum in the optical range that follows the relationship
- [math]\displaystyle{ \frac{1}{\lambda} = \frac{4}{B}\left(\frac{1}{2^2} - \frac{1}{n^2}\right) = R_\mathrm{H}\left(\frac{1}{2^2} - \frac{1}{n^2}\right), n=3,4,5,... }[/math].
This relation was found by Johann Balmer and was later generalized by Johannes Rydberg. RH is the Rydberg constant for hydrogen, [math]\displaystyle{ \lambda }[/math] is the observed wavelength of one of the lines, and n is an integer corresponding to that particular line as well as the principal quantum number of the excited electron state that produces the line. The Balmer lines are produced by absorption or emission of electromagnetic energy due to changes in the excitation level of the hydrogen atom between the first excited state and higher energy states.
To make meaningful measurements, we calibrated our instrument by taking wavelength measurements of emission lines of mercury vapor. The emission lines of mercury vapor are well known so we compared the values we measured to the accepted values for the emission spectrum of mercury to come up with a calibration curve that related the values our instrument gave us to an actual wavelength.
Next, we measured the wavelength of hydrogen's spectral lines. After converting our measurements to actual wavelengths, we used Rydbergs's generalization of the Balmer equation to figure out the Rydberg constant for hydrogen. Our data and calculations showed that [math]\displaystyle{ R_\mathrm{H} = 1.10592*10^7 \pm 9.64*10^5\,\mathrm{m}^{-1} }[/math] in excelent agreement with the accepted value [math]\displaystyle{ 10 967 758.341 \pm 0.001\,\mathrm{m}^{-1} }[/math]