Physics307L F07:People/Joseph/Formal Lab Report

Determination of the Charge of a Single Electron, by way of Millikan's Oil Drop Experiment

Nikolai Joseph University of New Mexico Albuquerque, NM njoseph@unm.edu

Abstract

^{SJK 00:56, 7 December 2007 (CST)}

The Millikan Oil Drop Experiment was a landmark experiment in physics because it was the first time the charge of the electron was experimentally found. The experiment consists of measuring the time it takes for one drop of oil to fall some distance under the influence of gravity and then the time it takes to rise when subjected to an electric potential. With that data and some theoretical backup, the charge of the electron can be found. We took the data and measured the charge of the electron to be [math]\displaystyle{ e=1.85\times10^{-19} C }[/math], which differs slightly from the accepted value of [math]\displaystyle{ 1.602\times10^{-19}C }[/math], possibly due to human mental strain and inexact pressure determinations.

Introduction

^{SJK 02:06, 29 November 2007 (CST)}

The electron sits high in the world of particles and is fundamental to understanding the physical universe. Understanding the charge gives an explanation of how particles interact and the structure of matter. Determining the charge allows accurate calculations of fundamental interactions between matter and electro-magnetic fields. Determining the charge can be done by allowing droplets of oil to fall through an electric potential and measuring how much the potential moves the droplet. Through using values and are known (or can be easily determined from experiment), we can deduce the true charge of the electron.

Method

^{SJK 01:30, 29 November 2007 (CST)}

To measure the charge of the electron the influence on the electron by a known electric potential was used. We measured the times that it took for the droplet of oil to fall a known distance ([math]\displaystyle{ l=1.0\times10^{-3}m }[/math]) solely under the influence of gravity. We then applied the electric potential ([math]\displaystyle{ V=500 volts }[/math]) and measured the time it took for the droplet to rise over that same distance. Doing this multiple times generated the data necessary to compute the charge of the electron.

Equipment

^{SJK 01:33, 29 November 2007 (CST)}

01:33, 29 November 2007 (CST)
For everything that is possible, you need to put the company and model # (Millikan apparatus, power supplies, etc.)

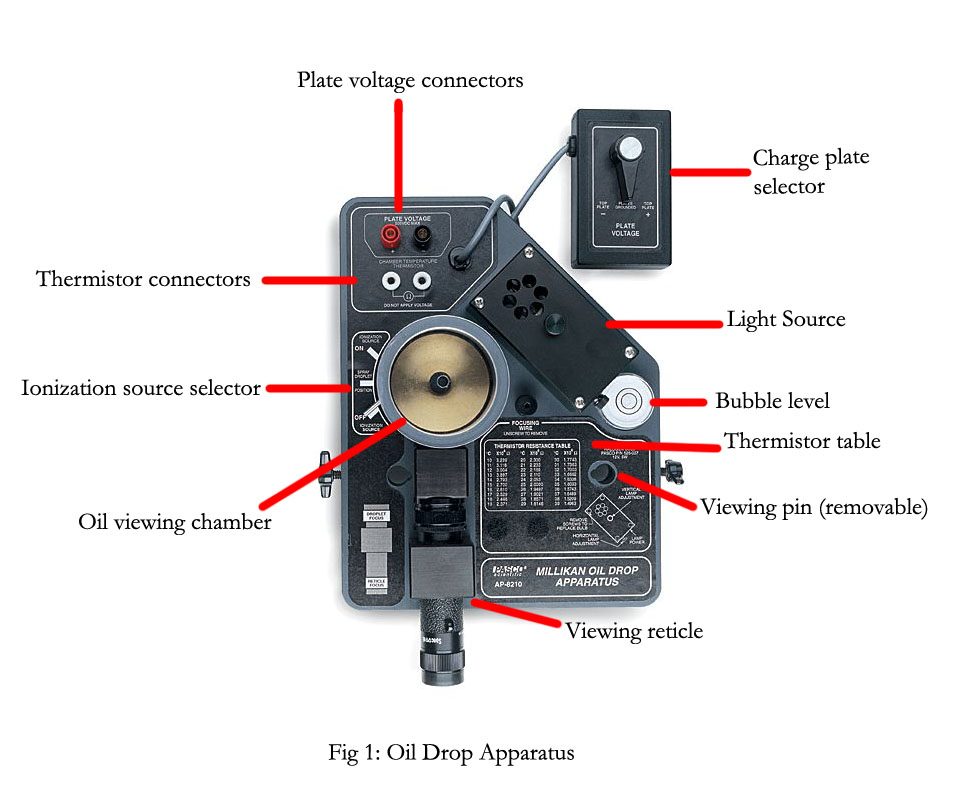
The experiment centered around the use of the Millikan Oil Drop Apparatus (Pasco AP-8210). Ssee fig 1 or look at the [manual]). There was also:

1. TEL-Atomic 50V-500V power source: connected to the Millikan Apparatus via BNC cables.
2. multimeter #1: connected to the Millikan Apparatus via BNC cables to show what voltage was being applied to the plates that when a acurrent was applied, would cause the electron to rise
3. multimeter #2: : connected to the Millikan Apparatus via BNC cables indicated the voltage through the thermistor
4. stopwatch or stopwatch applet: for recording the rise and fall times
5. atomizer: for spraying the oil in a fine mist into the oil chamber
6. mineral oil: the oil that would be divided into the actual drops that were being watched

Setup

^{SJK 01:32, 29 November 2007 (CST)}

01:32, 29 November 2007 (CST)
I changed all of your PNC to BNC, and then realized that acutally it wasn't BNC connections. I call them banana plugs...I'm assuming that PNC isn't a real term?

The apparatus needs to be on a level surface to remove as much uneven gravitational influence as possible. The apparatus was placed atop several textbooks, to provide a more suitable viewing height, and was leveled using the adjustable screw legs and a bubble level on the device. The power supply was connected to the ports labeled "Plate voltage" on the apparatus and multimeter was plugged into the power supply to allow the voltage through the plates to be known. The light source was plugged into the wall, and it had no switch; the light was on only if the cable was plugged in. BNC cables connected the port labeled "Chamber Temperature" to a multimeter that displayed the voltage through the thermistor. A table on the apparatus gave corresponding temperatures to voltages. The chamber could be disassembled by removing the outer housing, the droplet hole cover, the capacitor plates, and the spacer within it. The plates were cleaned and reassembled. The viewing reticle had to be calibrated and to do required the chamber be opened up and and the viewing pin needed to be inserted into the hole where the droplet hole cover was. With the light on, someone looked through the reticle and focus the reticle, using the focusing knobs, until the pin was as clearly visible as possible. Once this was done, the pin was removed and droplet hole cover was replaced, and the chamber was reassembled.

^{SJK 01:28, 29 November 2007 (CST)}

01:28, 29 November 2007 (CST)
This figure is awesome! Like I said elsewhere, I also want some more figures, and make sure those have descriptive captions.

Procedure

The first data to take was recording the thickness of the spacer. This was done with a micrometer and the attained value was [math]\displaystyle{ d=7.59\times 10^-3 m }[/math]. That value has use later on. The next step was to reassemble the chamber setup for data taking. Allow the power supply, light source, and thermistor all to warm up for a few minutes before beginning. The atomizer was filled with mineral oil of density [math]\displaystyle{ \rho=8.86\times 10^2 \frac{kg}{m^3} }[/math] (given by the manufacturer on the bottle). The ionization control was set to Spray Droplet position and the initial temperature of the thermistor was recorded. All overhead lighting was killed and one person looked through the viewing reticle. Before the oil was introduced all that was visible was the grid of the viewing reticle against a dim yellow-orange background from the light source. With a person looking, the other person put the atomizer so its tip was in the hole in the top center of the out housing. The person with the atomizer squeezer the bulb very quickly one time and allowed it to refill with air. Then another, much slower squeeze on the atomizer bulb, not allowing it to refill with air while it was still in the hole on the housing. During the second squeeze, the person viewing should see tiny, golden droplets fill the viewing area beyond the grid. This technique requires a degree of finesse and may take a few tries! During all of this the charging plate should be in the Plates Grounded position Once the droplets were all visible, the viewer would change the ionization source to Off. The viewer selects a droplet that is falling slowly, and is located so that the grid does not interfere with the visibility of the drop. The viewer tells the timer to begin timing as the drop passes one grid line and stop timing when it passes the next lower one. Following the same drop, the viewer applies a voltage from the charging plates, and records the time it takes for the droplet to rise. The ionization source can be turned to the On position and the thorium-232 source within the chamber will bombard the droplet with alpha particles, charging the charge on the droplet. This will causes the droplet to rise much quicker when a voltage is applied. It is very important that the same drop be followed. Collecting data for various droplets doing various things produces inconsistent and useless data. For the final calculations we need the air pressure. Unfortunately, published air pressures are always adjusted to sea level, whereas we are about 5300 feet above sea level. Making the conversion equation as: [math]\displaystyle{ \frac{P_1}{P_2}=\frac{P_x}{P_3} }[/math] With: [math]\displaystyle{ P_1 }[/math]=standard pressure at 5300 ft=833.756 hPA [math]\displaystyle{ P_2 }[/math]=standard pressure at sea level=1013.56 hPA [math]\displaystyle{ P_3 }[/math]=sea level pressure in Albuquerque on 12/5=1014.8 hPa [math]\displaystyle{ P_3 }[/math]=actual air pressure in albuquerque on 12/5 Finding P_1 took a trick I used the standard air pressure at 5000 feet, 843.08 hPA, and the standard air pressure at 6000 feet, 812 hPA. Added then and mulitplied by .3 and subtracted that total value from the pressure at 5000 feet. Doing everything I got the number 834.78 hPA

Data

^{SJK 02:01, 29 November 2007 (CST)}

Following a total of 8 droplets that were followed, we determined it only relevant to use the data from 6 of the droplets. This was not reckless abandonment of data though, There was a strong systematic tendency for the drops to drift behind the coordinate grid and they became very difficult to see. So difficult in fact, that it was determined that any measurements recorded whilst the droplet was obscured from sight was far too unreliable to be of any worthwhile contribution. Below is the listed useful data. The data is structured as follows:

[math]\displaystyle{ V }[/math]: The potential that was applied to create the repulsive electric field, volts ([math]\displaystyle{ V }[/math])
[math]\displaystyle{ T }[/math]: The temperature within the viewing chamber, in degrees Celsius (°C)
[math]\displaystyle{ t_f }[/math] (s): The fall time of the droplet, in seconds (s)
[math]\displaystyle{ t_r }[/math] (s): The rise time of the droplet, in seconds (s)

Droplet 1

[math]\displaystyle{ V }[/math]=+503V
[math]\displaystyle{ T }[/math]=23°C

[math]\displaystyle{ t_f }[/math]	47	49	51.3	45.5	43.9
[math]\displaystyle{ t_r }[/math]	4.5	4.6	4.8	4.9	4.8

Droplet 2

[math]\displaystyle{ V }[/math]=-503V
[math]\displaystyle{ T }[/math]=26°C

[math]\displaystyle{ t_f }[/math]	59.2	60.1	69.9	62.6
[math]\displaystyle{ t_r }[/math]	9.6	9.3	9.3	9.1

Droplet 3

[math]\displaystyle{ V }[/math]=-504V
[math]\displaystyle{ T }[/math]=27°C

[math]\displaystyle{ t_f }[/math]	42.3	47.2	50.8	47.1
[math]\displaystyle{ t_r }[/math]	12.1	12.1	12.9	13.5

Droplet 4

[math]\displaystyle{ V }[/math]=+505V
[math]\displaystyle{ T }[/math]=27°C

[math]\displaystyle{ t_f }[/math]	57.5	63.5	63.0
[math]\displaystyle{ t_r }[/math]	10.0	9.7	9.1

For droplets 5 and 6 I am listing only the first few measurements. The complete data sets for these two droplets maybe be found in the Appendix.

Droplet 5

[math]\displaystyle{ V }[/math]=+500.2V
[math]\displaystyle{ T }[/math]=22.6°C

[math]\displaystyle{ t_f }[/math]	11.5		63.0
[math]\displaystyle{ t_r }[/math]	10.0	9.7	9.1

Calculations and Results

The target value to be determined is the charge of the electron, [math]\displaystyle{ q }[/math]. Here are the necessary equations and values used in doing the calculations for [math]\displaystyle{ q }[/math]:

Values

^{SJK 01:42, 29 November 2007 (CST)}

01:42, 29 November 2007 (CST)
Actually, some of these aren't "known," for example, the spacer you measured, and the air pressure you looked up somewhere (and explain that it's converted from the sea level value for our altitude)? You should look up the actual air pressure from that day and / or explain that day to day changes don't matter too much, if they don't.

[math]\displaystyle{ \rho=8.86\times 10^2 \frac{kg}{m^3} }[/math] (density of the mineral oil)
[math]\displaystyle{ g=9.8 \frac{m}{s^2} }[/math] (gravitational acceleration)
[math]\displaystyle{ p=8.5\times10^4 Pa }[/math] (air pressure)
[math]\displaystyle{ l=1.0\times10^{-3} m }[/math] (length droplet will be measured over)
[math]\displaystyle{ b=8.20\times10^{-3} Pa\cdot m }[/math] (proportion constant)

Determined

[math]\displaystyle{ T }[/math] (temperature from thermistor in °C)
[math]\displaystyle{ V }[/math] (Voltage between plates in viewing chamber in volts)
[math]\displaystyle{ t_f }[/math] (fall time in seconds)
[math]\displaystyle{ t_r }[/math] (rise time in seconds)
[math]\displaystyle{ d=7.59\times 10^{-3} m }[/math] (width of the plastic spacer)

Equations

^{SJK 01:36, 29 November 2007 (CST)}

[math]\displaystyle{ \eta }[/math] (viscosity of air as a function of T found in a table in Pa*s)
[math]\displaystyle{ v_f=\frac{l}{t_f} }[/math] (average velocity of oil droplet falling in no field in m/s)
[math]\displaystyle{ v_r=\frac{l}{t_r} }[/math] (average velocity of oil droplet rising in a field in m/s)
[math]\displaystyle{ a=\sqrt{\left(\frac{b}{2p}\right)^2+\frac{9\eta v_f}{2g\rho}}-\frac{b}{2p} }[/math] (radius of droplet in meters)

Which all contribute to: [math]\displaystyle{ q=\frac{4}{3}\pi\rho g d\frac{a^3}{V}\frac{\left(v_r+v_f\right)}{v_f} }[/math] (charge on oil droplet in Coulombs)

^{SJK 01:40, 29 November 2007 (CST)}

01:40, 29 November 2007 (CST)
"Plugging in and sorting out all necessary values..." is pretty informal. This table is very nice, especially the reporting of the (uncertainties). You do need more figures in your paper. One idea (which I like) would be to plot a scatter plot of **all** the rise and fall time measurements. You could make the x-axis "droplet number/rise" and the y-axis "fall time", and then you'd have a cluster of dots for each. Then you could color code any data that are thrown out. or maybe you can think of an better way of displaying all the data, but that would be very nice.

Plugging in and sorting out all necessary values, the calculations are summarized as follows.

Droplet/Charge	[math]\displaystyle{ \eta\left(\times10^{-5} Pa\cdot s\right) }[/math]	[math]\displaystyle{ v_f\left(\times10^{-5} \frac{m}{s}\right) }[/math]	[math]\displaystyle{ v_r\left(\times10^{-4} \frac{m}{s}\right) }[/math]	[math]\displaystyle{ a\left(\times10^{-7} m\right) }[/math]	[math]\displaystyle{ \left\| q\right\|\left(\times10^{-19} C\right) }[/math]	Estimated Multiple of [math]\displaystyle{ e }[/math]
1A	1.83	2.17(17)	2.11(7)	4.08	4.00	2
2A	1.85	1.60(12)	1.07(2)	3.46	1.75	1
3A	1.86	2.14(16)	0.79(4)	4.09	1.76	1
6A	1.86	1.63(9)	1.04(5)	3.52	1.75	1

Where the uncertainty is in a value is in parenthesis.

Conclusion

^{SJK 01:47, 29 November 2007 (CST)}

01:47, 29 November 2007 (CST)
These calculations are still the meat of your report, and should go in the "results and discussion" section.

Also, take a look at Kyle's page. Because this is your formal report, I want you to come up with a way of getting a final answer without relying on the known value (to compute your suspected number of electrons). This will be easier with your extra data you will acquire.

Also, you do a great job reporting uncertainties above, but do not have uncertainties in your final answer! You will need to figure out how to do this (talk to me and others).

With several suspected values of [math]\displaystyle{ e }[/math], we can determine our own [math]\displaystyle{ e }[/math] and see how close it is the actual value. It is reasonable to sum all suspected [math]\displaystyle{ q }[/math]'s and set them equal to the sum of the respective suspected value of [math]\displaystyle{ e }[/math]:

[math]\displaystyle{ \sum \left|q\right|=\left(4.0044+1.7533+1.7582+1.7539\right)\times10^{-19} C =\left(2+1+1+1\right)e }[/math]

Solving for [math]\displaystyle{ e }[/math]:

[math]\displaystyle{ e=1.85396\times10^-19 C }[/math]

If the true value of [math]\displaystyle{ e }[/math] is [math]\displaystyle{ 1.602176\times10^-19 C }[/math], then the error on the experiment was:

Error=[math]\displaystyle{ \frac{\left|1.602176\times10^{-19}C-1.85396\times10^-19 C\right|}{\left|1.602176\times10^{-19}C\right|}=0.157=15.7% }[/math]

^{SJK 01:49, 29 November 2007 (CST)}

01:49, 29 November 2007 (CST)
This section is a little informal, but you also have zeroed in on good ideas...and they all are correctable! I like the idea of having the person who is observing also be the one to operate the stopwatch. And you can definitely look up the air pressure exactly for that day and time (or maybe use a barometer in the lab???). You should pursue all of these next week.

This is quite close, but not exact. There are several possible sources of the error here. A first, and obvious, choice is the values for air pressure and viscosity are probably inexact. This experiment was not performed in nearly a controlled enough environment with optimal geographic conditions. Another source of error is the timing. One person seeing something, calling out "start" and "stop!", and the other person hearing this, then pushing the button; there are very many problems here. One person may not have good hearing, or quick enough reaction times, or any other number of problems. The least problematic system might be the observer having a button that starts and stops the timer, and having someone else record the times from the timer. This cuts down on potential delays. For having such obvious problems, the experiment still produced a very reasonable value with error that is in the manageable range.

References

1. [1] 2. Elementary Charge, [[1]] 3. [2] [PASCO Scientific Model AP-8210] <reference /> http://physics.nist.gov/cgi-bin/cuu/Value?e%7Csearch_for=elecmag_in!

^{SJK 01:59, 29 November 2007 (CST)}

01:59, 29 November 2007 (CST)
You don't have an Acknowledgments section!

Good job with the one original reference. Once you expand your introduction, you will have many more to list here. It's an important part of a scientific paper.

Koch comments

See above
Some major things:
- Expand introduction
- Include more citations to original research
- Missing items (title, etc.)
- Uncertainty on final answer
- Take more data with Bradley. Use extra data taking to:
  - implement your suggestions for improvements
  - improve data analysis method (not relying on known value)
  - hopefully get more precise answer