Physics307L:People/Martin/Notebook/071024
Millikan Oil Drop
Purpose
to experimentally determine the electric charge and look for a quantization of this charge.
Materials
Here is the manual we used PASCO manual.
- apparatus platform and plate charging switch
- 12V DC transformer for the light
- atomizer to spray the oil
- Squibb #5597 oil (intestinal lubricant)
- A 500V power supply to charge the plates
- Multimeter to measure voltages and resistances
- Stopwatch
- Banana cables
- A micrometer
Setup
- Level apparatus using the attached bubble level
- Disassemble the droplet viewing chamber and measure the plate spacer with a micrometer
- connect the halogen light and the voltage source to the apparatus through a multimeter to measure the voltage.
- Fill atomizer with oil
- Focus the viewing scope using the focusing needle (explained in the manual)
- measure the thermistor resistance to find the temperature of the viewing chamber.
Theory
- A particle that has reached its terminal velocity has no total force acting on it. For the oil drops which are in free fall this is where the gravitational force is equal to the air resistance force. [math]\displaystyle{ mg = kv(fall)\ }[/math].
- In an electric field (if the particle has a charge) the summation of forces equation becomes [math]\displaystyle{ Eq = mg + kv(rise)\ }[/math].
- We need to find q so eliminating k we get [math]\displaystyle{ q = mg\frac {v(fall) + v(rise)}{Ev(fall)} }[/math].
- We know that [math]\displaystyle{ m = \frac{4}{3}\pi\ a^3\rho }[/math]
- Using stokes law to find a we get that [math]\displaystyle{ \alpha=\sqrt{\frac{b^{2}}{{4p}^{2}}+\frac{9nV_f}{2g\rho}}-\frac{b}{2p} }[/math]
- Finally we get :[math]\displaystyle{ Q=\frac{4}{3}\pi\rho g\left(\sqrt{\frac{b^{2}}{{4p}^{2}}+\frac{9nV_f}{2g\rho}}-\frac{b}{2p}\right)^{3}\frac{\left( V_f+V_r\right)}{EV_f} }[/math] by substituting a and m.
Known Values and Setup Measurements
- Thermistor resistance: [math]\displaystyle{ R = 2.387\; M \Omega }[/math], which implies temperature [math]\displaystyle{ T = 19 ^{\circ}\;C }[/math]
- Spacer thickness: [math]\displaystyle{ d = 7.59\;mm = 7.59 \times 10^{-3}\;m }[/math]
- Oil density: [math]\displaystyle{ \rho = 886 \;\frac{kg}{m^3} }[/math]
- Barometric Pressure: [math]\displaystyle{ P = 8.5 \times 10^4\;Pa }[/math]
- Gravitational Acceleration: [math]\displaystyle{ g = 9.8\;\frac{m}{s^2} }[/math]
- Some constant for determining radius of drop in m: [math]\displaystyle{ b = 8.20 \times 10^{-3}\; Pa \cdot m }[/math]
- Voltage across the plates: [math]\displaystyle{ V = 503 }[/math]
these values were copied from my lab partners sheet
Procedure
- Spray droplets into the viewing chamber (take the spray nozzle away from the hole before releasing the sprayer, you will suck the droplets back out).
- Look through scope to find a falling droplet (make sure it is not moving too fast)
- Assure that the droplet had a charge (flip the switch to charge the capacitor and look for a charge)
- Measure the time it takes for a droplet to travel a known distance on the apparatus grid.
- Flip the switch and measure the rise time of the same droplet.
- Repeat the last two steps at least ten times. (this didn't happen in my experiment)
Data
All of my data can be found on this excel sheet it is all labeled (plus all of the calculations are done here using the above equations and constants). File:Millikan sheet.xls
Results
All of the work described is done in my Excel file.
SJK 01:20, 19 November 2007 (CST)

Very nice method! Jesse gave you props in his lab summary for using this linear fit method, which I think is very clever!
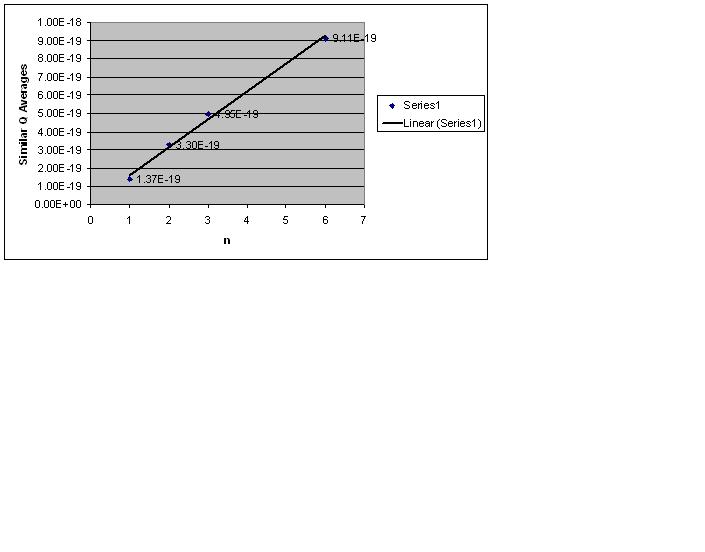
After calculating the charges on the individual oil droplets I assumed that they were quantized (I had this advantage on Millikan knowing that charge was a quantized quantity). The drops centered around 4 numbers, I averaged these numbers and I took the smallest of these averages and divided the other three by the smallest average. I rounded to the nearest whole number and graphed a plot with the nearest whole number as the x-axis and the averages of the charges as my y-axis. The slope of this line would be my fundamental charge (e) [math]\displaystyle{ Q = n e }[/math].
Using this and excel to calculate the error in calculating slope I got:
- fundamental charge (e): [math]\displaystyle{ 1.52 \times {10}^-19 C }[/math]
- The uncertainty in this calculation: [math]\displaystyle{ 8.04 \times {10}^-21 C }[/math]
- Accepted value for e: [math]\displaystyle{ 1.6 \times {10}^-19 C }[/math]
- Relative error: 5%