Physics307L:People/Muehlmeyer/Poisson
Poisson Distribution Summary
Introduction
In this lab we have set out to show the natural occurrence of the Poisson distribution when "counting" random events. We will use cosmic radiation that we detect using a scintillator whose signals are amplified by a photomultiplier as our radom events. Using a computer to count the number of events (cosmic ray events) per set amount of time called the "dwell time", we will show that the Poisson distribution is a result. What this will show is that "random" events occur at a rate that we can plot, and we will see that the rate of these occurences are not so random...they turn out to fit very predictable patterns with a definite average rate.
The Poisson distribution :[math]\displaystyle{ f(k; \lambda)=\frac{\lambda^k e^{-\lambda}}{k!},\,\! }[/math] is a probability distribution for discrete, independent events. It is a function that outputs the probability of obtaining result k after you have done the "counting" experiment. k is the number of occurences. λ is the average rate of those occurences.
Set Up
An extensive description of our set up can be found in our lab notes Notes Poisson Distribution Lab
The cosmic radiation received through the scintillator is amplified by the photomultiplier then further amplified by an outboard amplifier which then inputs into a software event counter in the computer. The event counter records the number of "events" (signals from the photomultiplier) per dwell time and does this so many times n (we set n to be 512).
Our set up gives us reason for concern. We had extensive difficulties being able to even receive a signal stong enough, and of which we could amplify. Another thing of importance to note here is our deviation from the procedure outlines in Gold's Lab Manual, we did not use the "lead cave". Our scintillator was not shielded, and thus will receive more events per time then in previous experiments.
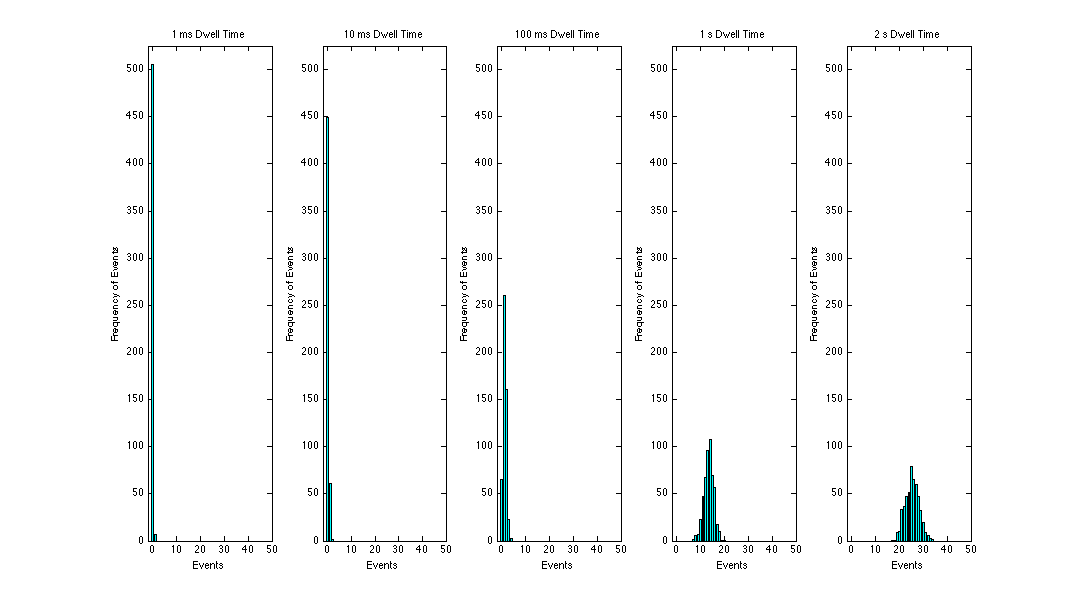
Event Plots
Plotting our results from the counting software our results were as follows for each dwell time:
Analysis
The Poisson distribution is characterized by the fact that the standard deviation is equal to the square root of the mean λ. If we can show that this is the case for our data (or atleast reasonably close), then we have shown that our data is in fact a manifestation of the Poisson distribution.
Calculating the mean:
λ is the expected rate of events, the expected number of occurences per time interval. To calculate λ I will use the data average method. I sum up the number of events that occurred, and divide by the number of times I took those events.
- [math]\displaystyle{ \widehat{\lambda}_\mathrm{MLE}=\frac{1}{n}\sum_{i=1}^n k_i. \! }[/math]
The following is a summary of my λ values for each dwell time using the data average method.
SJK 10:26, 20 October 2008 (EDT)

This table is a great analysis idea
| Dwell Time Δt | Frequency Count λ | λerror |
| 1 ms | λ = 0.013671875 | 4.05974132e-7 |
| 10 ms | λ = 0.126953125 | 1.7313458323e-5 |
| 100 ms | λ = 1.294921875 | 4.62059546375e-4 |
| 1 s | λ = 13.48828125 | 3.25904896073e-4 |
| 2 s | λ = 25.36132813 | 2.4259613547e-4 |
This makes sense, as our dwell time increases, our average rate of events increases. And when you compare each of these values to our plots, they are quite apparently the mean.
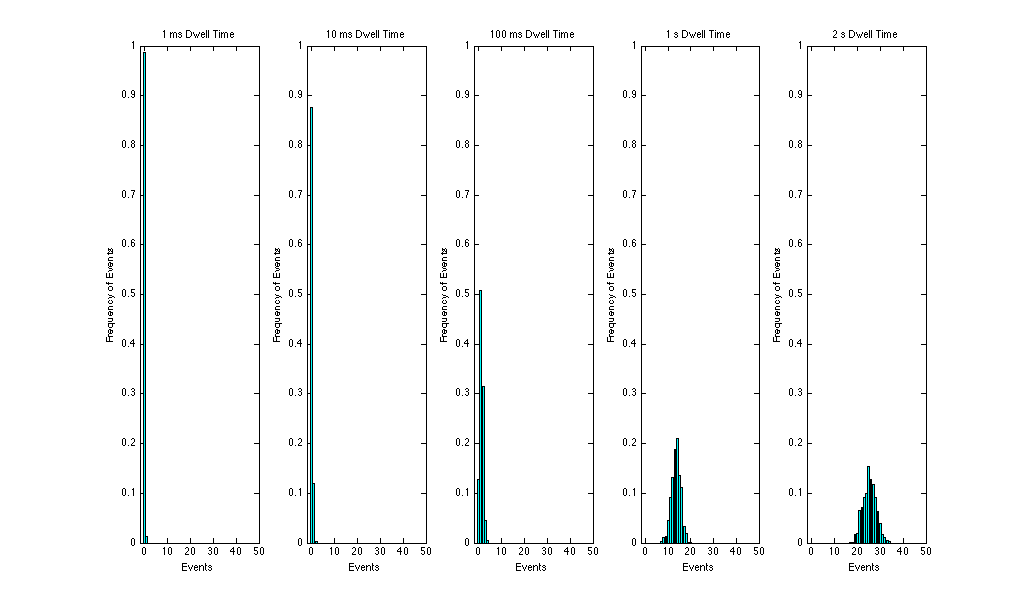
In order to see our results more clearly, we can normalize our results so that they fit a probablity density function that sums to 1. This plots our results as a matter of probabilty. We do this by dividing the frequency of events by the maximimum possibility 512. See the plots below.
What is most interesting is that as we increase the dwell time the histogram plot begins to look like a Gaussian function. The Guassian function peaks at some median value that represents the most common rate of occurences. If we allow for more events (higher dwell time) the histogram then is a plot of this Guassian funtion, which tells us their is a rate of events that occurs the most, and that rate is that at which the Guassian peak appears, our mean, λ.
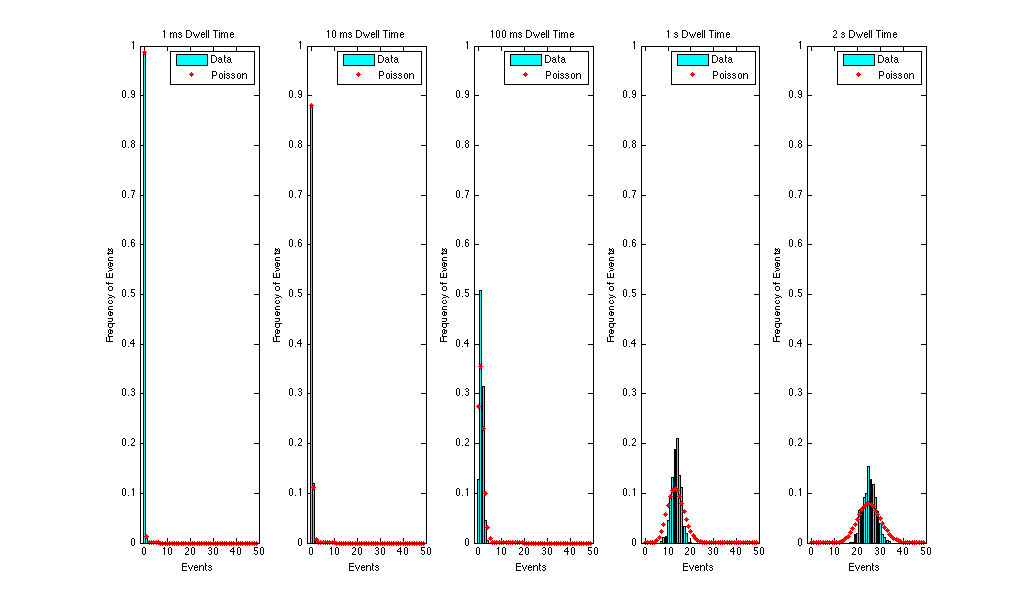
Fitting our Data to the Poisson Distribution
How close are our results to the ideal Poisson distribution?
The Poisson distribution is characterized by the fact that the standard deviation is equal to the square root of the mean λ. If we can show that this is the case for our data (or atleast reasonably close), then we have shown that our data is in fact a manifestation of the Poisson distribution.
First I will find the standard deviation by assuming that our data is in fact a Poisson distribution (I will take the square root of our calculated λ values) and I will call this σk = [math]\displaystyle{ \sqrt{\lambda} }[/math]. Comparing σk to the actual standard deviation of our data σx will tell us how close our data is to the ideal Poisson distribution.
| Dwell Time Δt | σk | σx |
| 1 ms | 0.11692 | 0.116238308 |
| 10 ms | 0.35650 | 0.344790832 |
| 100 ms | 1.13795 | 0.766810045 |
| 1 s | 3.67264 | 2.066378743 |
| 2 s | 5.03600 | 2.945079248 |
How close are σk and σx?
My numerical analysis in the chart above shows that the widths (σ values) of the ideal and actual for low dwell times are quite accurate, but as our dwell time increases, the ideal Poisson becomes wider than our actual data.
σ is a measure of the width of our distribution. It is apparent that for high dwell times the width of the ideal Poisson is greater than the width of our actual data. A graphical expression of this was beautifully done by my partner Alexander Barron:
For low dwell times σx is very close to σk, but as we increase our dwell time the two values begin to differ a bit more. However, I think it is still safe to say that the two values are reasonably close enough to be considered a Poisson distribution.
Why do the two values of σ differ for higher dwell times? Since σ is a measure of deviation of the values from their mean (dispersion), I think that this could be explained by the simple fact that outlyers occur more frequently with longer dwell times, which throw off our data from the ideal Poisson distribution.SJK 10:23, 20 October 2008 (EDT)

But it doesn't seem like outliers are affecting your distribution (the mean seems pretty well centered)...it really does look like your distribution is more predictable that it should be...and it's tough to think of reasons that may be the case. One idea that comes to mind is if you somehow got the equipment set up to count two events as one...but no idea how that would have been achieved
Conclusion
The data collection of "random" cosmic radiation events proved to fit the Poisson distribution reasonably well. We also saw how, as we increase the dwell time, this distribution begins to fit a Gaussian with an obvious average rate. We showed our selves that our data is characterized by the fact that the standard deviation can be approximated to the square root of the mean λ, which is a characteristic of the Poisson distribution.
- Justin Roth Muehlmeyer 11:37, 12 October 2008 (EDT):