Physics307L:People/Benedict/Draft
An Accounting of the Sources of Error in the Determination of the Charge to Mass Ratio for the Electron Using the Fine Beam Tube Method
SJK 00:21, 18 November 2010 (EST)

Good title, author, contact
Abstract
SJK 00:37, 18 November 2010 (EST)

I like the abstract. Some fine points: (1) is it the fine beam method that is problem, or is it (a) need for helium and (b) doing the circular geometry thing, instead of trying to balance the B-field force with a countering E-field. (See Klimov's report for discussion of this, 2008 I think.) (2) I didn't actually see a discussion of the heater energy (3) If you're going to make a claim at the end of the report (i.e., that you think you know the major source of syst. error), then you may as well end your abstract with saying that.
The determination of the e/m ratio for the electron using the fine beam method is well known to be prone large systematic errors. In this paper we will present an account of a typical lab using this method, and the common method of determining e/m from experimental observations. We will then explore the effect of changing any of the 3 parameters in the common model, to see how large of an effect small changes in observed voltage, current, and radii of curvature would have to account for error in the experimental observation of parameters used in the calculation of the e/m ratio. We then explore corrections to the model for relativistic effects, energy loss from collisions of the electrons with the helium gas, and for the work done by the heater in releasing the electrons.
Introduction
SJK 00:54, 18 November 2010 (EST)

This is a good introduction, a little on the concise side. On the other hand as I mentioned below, your style here is more like a brief letter. I'd add another paragraph introducing your measurement method and that you'll be trying to locate the systematic error (basically what you say in the abstract). As of now, this is more like just the history. If you could find an original paper that uses this circular beam method that would be great. That would be good to get another citation to a peer-reviewed report, right now you only have two that are original peer-reviewed research.
The first investigation into the determination of the charge to mass ratio of the electron was performed by J.J. Thomson[2] around 1897, his results were communicated on Friday, April 30[4]. One of the first uses of the ratio was in approximating the mass of the electron, which was found to be almost on the order of an atom[4]. This was taken as proof that atoms are composed of smaller particles that compose cathode rays. More precise measurement of the charge of an electron was made by Millikan in his famous experiment[3], which lead thanks to the e/m ratio already known to a more accurate measurement of the mass of an electron. Accurate measurement of these fundamental constants was useful in proving the predictions of the then new field of quantum mechanics, which predicted the energy levels of hydrogen and those predictions required accurate values for the charge and mass of the electron. Overall the charge to mass ratio is a useful quantity, and accurate determination of it is valuable even today.
Experiment and Materials
Materials and Assembly
SJK 01:07, 18 November 2010 (EST)

Methods are typically not written in this present tense and "how to" fashion. It's more "we did ___" style. Also, for whatever reason a list of supplies is not given, but it is worked into prose form. See this paper for an example.
The materials used in this lab consists of three power supplies:
- Gelman Deluxe Regulated Power Supply, 6-9V 2A
- Soar DC Power Supply model PS 3630, 6.0V 1.5A
- Hewlett Packard 6236B, 150-300V 40mA
Three Digital Multimeters, two for measuring voltage, one for current. And most importantly, Uchida Yoko e/m Experimental Apparatus model TG-13.

The e/m experimental apparatus is just a tube filled with helium gas a low pressure, and containing a device for heating a filament to release electrons which are accelerated by a generated electric field. Then the accelerated electrons are exposed to a magnetic field, through the pair of Helmholtz coils on the device. The applied magnetic field produces a Lorentz force on the electrons which causes them to move in a circle. Information on the assembly of the materials can be found in [1].
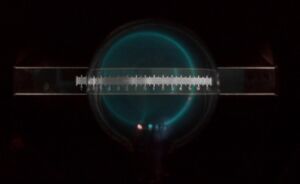

Procedure and Methods
SJK 01:09, 18 November 2010 (EST)

This section is a good example of why methods are usually "we did." You say the measurement "is best performed as..." but is that what you did? Probably, but it's not clear. How long did you actually wait for the filament to heat up? etc.
For this lab the procedure is to first turn on the power supply connected to the filament heater, as it takes about 3 minutes to heat up. Then set the accelerating voltage to a reasonable starting voltage, about ~200V, and the current to the Helmholtz coils to ~1A. Then take measurements of the radius of curvature of the beam, for a constant current and varying potential, and for a constant potential and a varying current. Measurement of the radius of curvature is best performed by measuring it on both sides of the ruler and averaging the values to correct for parallax.
Results and Discussion
SJK 01:11, 18 November 2010 (EST)

As I mentioned, your format here is different than usual. I don't want you to change that, instead on want you to focus on the remaining mysteries and approaching the questions I brought up. I would like you to add at least one good data graph, though, so you can get some experience doing a figure that shows data, with a title and caption, etc. You could show one of the constant current or constant voltage graphs, for example.
The most common method for computing the e/m ratio for electrons starts with considering the kinetic energy of the electrons, given as usual by [math]\displaystyle{ T=\frac{1}{2}mv^2 }[/math], and we know the kinetic energy given to the electrons by the accelerating voltage such that [math]\displaystyle{ T=eV_{acc}=\frac{1}{2}mv^2 }[/math], which gives [math]\displaystyle{ v^2= \frac{2eV_{acc}}{m} }[/math]. The Lorentz force from the applied magnetic field has a magnitude of, [math]\displaystyle{ F=evB\sin \boldsymbol{\theta} }[/math], We also know that the magnetic field from the Helmholtz coils is perpendicular to the plane of the beam, such that [math]\displaystyle{ \sin \boldsymbol{\theta}=1 }[/math] where the B field is given by [math]\displaystyle{ B=7.80\times 10^{-4} \mbox {tesla/ampere}\, \times I }[/math], where I is the current. . We also know that any centripetal force is of the form [math]\displaystyle{ F=\frac{mv^2}{r} }[/math] where r is taken as the radius of curvature in this case. Putting this all together gives, [math]\displaystyle{ \frac{e}{m}=\frac{2V_{acc}}{B^2r^2} }[/math] we will always assume from here on that r is measured in cm, B in tesla, and Vacc in volts.
Using Data which can be found here e/m Lab Notebook, the results of using the data and directly calculating e/m gives an average value of [math]\displaystyle{ \frac{e}{m}= (2.17\pm .02) \times 10^{11} \frac{C}{Kg} }[/math], which is a relative error of 23.6% and a fractional error of 0.9%. Forming a least squares fit of the data for the constant current, varying voltage or for varying current and constant voltage gives similar results, which leads to the conclusion that the majority of the error in the measurement of e/m must be systematic error. This means that either the method of measuring the values used is flawed, or that the model used to attain the value is flawed. We will now explore these two scenarios.
We begin by estimating the amount of error introduced by taking poor quality measurements, and checking their magnitudes. To start we form a function which will give us the observed value for e/m for given values of the error of the radius, B field, and voltage, such that [math]\displaystyle{ F(r_e,B_e,V_e)= \frac{2*(V_{acc}+V_e)}{(B+B_e)^2(r+r_e)^2} }[/math], where [math]\displaystyle{ (r_e,B_e,V_e) }[/math] are taken to be the error in the measurement of the radius, the B field, and the accelerating voltage respectively. We then take the taylor series of the function and keep only term of the first order, since we will assume all measurement errors to be small getting, [math]\displaystyle{ F(r_e,B_e,V_e)\approx \frac{2*V_{acc}}{B^2r^2} + \frac{2*V_{e}}{B^2r^2} - \frac{4*V_{acc} * B_e}{B^3r^2} - \frac{4*V_{acc} * r_e}{B^2r^3} }[/math]. This then gives us an error function [math]\displaystyle{ E(r_e,B_e,V_e)= \frac{2*V_{e}}{B^2r^2} - \frac{4*V_{acc} * B_e}{B^3r^2} - \frac{4*V_{acc} * r_e}{B^2r^3} }[/math]. now if we assume the we are only off by small amounts, then typical values of the error of the radius of curvature would be about one tenth of a centimeter, the typical error of the B field would be about 0.00001 T, and typical error in the voltage would be about 5 volts. Then the magnitude for error given average values of r of 5cm, B of 0.00117 T, and Vacc of 200V, would be 1.66% of the magnitude of the actual value of e/m for voltage, 1.13% for the B field, and 2.56% for the radius. In the worst case measurement error could account for about 5% of the total error. Which makes it an important contribution to the error, but it still is short of the around 20% error typically attained while performing this experiment.
We can also use the above error function to investigate the magnitude of the effect that the earth's magnetic field would have on the experiment. We know that the strength of the Earth's magnetic field is about 5*10^-5 T, and using that value in the error function would give an error of about 5% in the calculation of e/m.
We must then investigate contributions to the measurement error from sources not included in the model typically used. We first begin with the obvious problem of the energy loss due to collisions of the electrons with the helium particles. We know from the manual for the device, which is obtainable from the Pasco Scientific website(Pasco just resells the Uchida Yoko TG-13 as the SE-9638) that the pressure of the helium gas in the Fine Beam Tube is about 10^-2 mmHg, given the large imprecision in the value given, we will assume that it is about 2 Pascals to make the following calculations simpler. From this we can find the mean free path of the gas given that the average diameter of the helium molecule is 0.98 Angstrom, and that the temperature is about 300 K using [math]\displaystyle{ l=\frac{kT}{\sqrt{2} \pi d^2 p} }[/math], where k is boltzmann's constant, T is temperature, d is the diameter of the particles, and p is the pressure. This gives [math]\displaystyle{ l \approx 4.7 cm }[/math].
SJK 00:31, 18 November 2010 (EST)

This is an interesting approach! But I'm going to question it the most. I'd like you to devise ways of testing your theory during the extra data week. Here's my questioning: Doesn't the mean free path refer to the average path of a helium atom to travel before colliding with another helium atom? That is: it doesn't refer to an electron. The electrons aren't undergoing random diffusion, they are zipping through the gas. Surely if an electron were close to at rest, it would travel no distance before a helium atom would collide with it. And if it were going very fast, it would almost be like shooting a bullet through a forest. It would interact with a number of helium atoms depending only on the density of helium, right? I think you should discuss this with Katie.
Secondly, just because the light we see is of approximately 500 nm, does that really indicate the average energy lost by the electron? As you know from the energy levels of neon experiment, an inelastic collision can exchange differing values of energy when above the ionization threshold (as you are). I can't see an obvious reason that the average collisional energy would be about 500 nm, though I do agree that's the color we see. Why we see that particular color remains a mystery to me. Andy why it's violet at lower energy is also a mystery.
My final question, and I know from discussion in class that you don't agree is that the beam radius depends on beam current. I know you disagreed, but neither of us actually turned on the instrument to check. I have seen this in the past: turn down the filament voltage and the beam gets smaller (I think). This would not be accounted for by the mean free path argument.
The mean free path is the average distance a particle can travel in the gas without colliding, so on average the electrons with travel about 4.7 cm before colliding and losing energy. Since the electrons are traveling in a circle of radius r, we know the total distance they travel, and so we can estimate the average number of collisions taking r as about 5 cm as [math]\displaystyle{ N \approx \frac{2 \pi r}{l} = 6.7 }[/math], so on average each particle experiences about 7 collision as it moves through the loop. We also know that the wavelength of light emitted from the collision is about 500 nm, using the relation [math]\displaystyle{ E= \frac{hc}{\lambda} }[/math] gives a typical energy of [math]\displaystyle{ E \approx 2.5 ev }[/math], which means on average, the electrons should lose about 18 ev of energy. We could then be justified in correcting the model to account for the energy loss, by taking the accelerating voltage as being 3.3*r volts less than it is measured, this is of course an over estimate but it is about the same order of magnitude as the actual effect. Given more precise measurement of the pressure of the helium gas, and knowing the temperature at which it was inserted would motivate a more careful analysis. However that information is not available at this time. This implies a new model for the calculation of the e/m ratio of [math]\displaystyle{ \frac{e}{m}=\frac{2(V_{acc}-3.3r)}{B^2r^2} }[/math].
Using this new model on the same original set of data gives a value for the e/m which improves the relative error by about 7%, and gives [math]\displaystyle{ \frac{e}{m} =(2.05 \pm 0.02)*10^{11} \frac{C}{Kg} }[/math].
Next is an investigation into whether relativistic effects would contribute in a meaningful way to the error in determining the e/m ratio. To see if relativistic corrections are going to be helpful we first determine the ratio of the velocity of the electrons to the speed of light, using [math]\displaystyle{ \frac{v}{c}=\frac{eBr}{mc} }[/math] which was used in the initial derivation, this gives [math]\displaystyle{ \frac{v}{c} \approx 0.027 }[/math] using B=0.00117 T, and r=4 cm. And since that is less than 10% of the speed of light, there is no need for taking relativistic effects into account.
The last reasonable source of error to investigate is the uneven acceleration of the electrons, given that there is a hole in the anode which would lead to a nonuniform electric field. This effect is much harder to take into account without accurate measurement of the electron gun assembly, which is unfortunately not available at this time. However this can be assumed to be large effect given that the dimensions of the chamber in which the cathode and anode are contained is around 2 cm long and about 1 cm in diameter(based on a rough attempt of measurement through the glass, and some estimation), even a tiny 1 mm hole in the anode would lead to a large change in the electric field in the gun. We will assume a 10% loss of voltage from this effect for the purposes of investigation, and motivated by the hole being about 10% of the size of the diameter of the assembly. Combining this with the above corrected model gives a new sample model of [math]\displaystyle{ \frac{e}{m}=\frac{2(0.9V_{acc}-3.3r)}{B^2r^2} }[/math]. Using this model with the same data set as before gives [math]\displaystyle{ \frac{e}{m} =(1.83 \pm 0.02)*10^{11} \frac{C}{Kg} }[/math], and a relative error of only 4%. This is a huge improvement over the simple model used in most experiments of this type.
Conclusion

Through a careful accounting of the sources of error in the experiment we were able to account for a significant percentage of the sources of error in the experiment. We were able to lower the relative error from 23% to just 4%, through corrections to the simple model used. There is still a need for further investigation of the sources of error, and more precise knowledge of the pressure of the helium gas and the temperature it was bottled at would help significantly. Along with a knowledge of the precise dimensions of the electron gun assembly, to aid in the estimation of the actual accelerating voltage. Unfortunately most of the records of such information would be held by the corporation that manufactured the device(Uchida Yoko), and their headquarters in Tokyo were unable to help when I tried calling.SJK 00:33, 18 November 2010 (EST)

Wow! You called Tokyo!
However, if anyone has a broken Uchida Yoko TG-13 tube lying around, and would like to measure those things that could be very helpful.
One of the more useful results of the above analysis is that the we were able to determine a reasonable estimation of the error in measuring the radius of the beam, and the relative effect of having an external magnetic field. There is also still a need for a more through investigation into the behavior of the beam in the low voltage, high current regime, which produces some odd effects.
Acknowledgments
SJK 00:49, 18 November 2010 (EST)

Good acknowledgements
I would like to thank Joseph Frye for the excellent pictures used in this paper. I would also like to thank Katie Richardson for the suggestion to investigate the mean free path in the gas.
References
SJK 00:46, 18 November 2010 (EST)

These seem like good references. Have you read them? You only need to be familiar with the parts that are relevant to what you're citing, to make sure you understand what information came from that paper. Since you'll have to have downloaded the PDF or read the HTML, you may as well put the link here so other peeps can do it as well.
1.M. Gold, Physics 307L: Junior Laboratoy, UNM Physics ans Astronomy (2006),[1]
2. J. Thompson, "Cathode Rays". The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, Vol 44, 293-316 (1897).
3.R. A. Millikan, "On the elementary electrical charge and the Avogadro constant". The Physical Review, Series II 2: 109–143 (1913).
4.GF Fitzgerald, "Dissociation of Atoms". The Chemical Educator, 1997. Springer.
Initial SJK Comments
Steve Koch 00:20, 18 November 2010 (EST): The format of this paper is different than we commonly see. However, it reads extremely well and is a very nice piece of work. So, I'm going to have to figure out how to make my comments as to the "formal" report part of it. It's more like a "letter" and an old-style letter that I usually really like. First, though, I will make some comments above about your different error estimates. It's gonna be fun, I think to try to test your hypotheses during the "extra data week"
Later comments
Steve Koch 01:16, 18 November 2010 (EST): Very nice rough draft! I would like you to make the revisions I note and also to focus on testing and pushing your hypotheses during the "extra data week." I have the one example above about the radius depending on beam current. Also, is it really a good idea to measure both sides? Why would you have parallax if you're aligning the beam with its own reflection on the ruler? Is the beam really a constant radius? Or is there evidence of a changing radius of curvature as it travels?