Physics307L:People/Barron/labsum~speedoflight
Speed of Light Lab Summary
Here is the lab manual page.
Here are my lab notes.
Partner: Justin Muehlmeyer
Introduction
This lab is fairly straight forward - we basically measure the time of flight of flashes from an LED pulse generator with a Time-to-Amplitude Converter (TAC). We take the voltage amplitude from the TAC for different distance measurements, then glean the value of c in air from the slope of a least-squares fit of x vs. t. The TAC is fed time pulses resulting from LED flash detection from a PMT. In order to vanquish the effects of changing light intensity due to changing distance between the pulse generator and the detector (known as "time walk"), we adjust the orientation of two polarizers between the two and attempt to retain constant output from the PMT.
Approach
We took four data trials:
1) large and increasing individual Δx over large total Δx,
2) small, constant individual Δx over small total Δx,
3) large, constant individual Δx over large total Δx, and
4) medium Δx with no time walk correction.
Final Results
SJK 01:31, 1 November 2008 (EDT)

Except for the fact that you have too many significant digits (thus making it a pain to read), this is a very nice table with nice graphs. I was easily able to assess your data and results quickly. Here is something to try: Take a look at your plots for trials 1, 2, 3. The upper and lower bounds are really quite far away from the data points. What kind of confidence interval do you think that would represent? Probably something like 99.99%, whereas you are implying a 68% confidence interval the way you report the data. Ask yourself as an experimentalist whether you think you computed the uncertainty correctly, judging by those graphs. In fact, plotting it the way you did was a really great idea--I just think you didn't stop to ask yourself whether it made sense looking at it. If you use the uncertainty from linear regression (see comments in your raw data notebook), I think you would find that the much lower uncertainty looks much more reasonable on these graphs.
NOTE: AXES ARE SET TO "TIGHT," SO SOME DATA POINTS ARE ON GRAPH EDGES
| Trial | Graphic Representation | Trial | Graphic Representation |
|
Trial 1:
Upper Error Bound:
Lower Error Bound:
|
|
Trial 2:
Upper Error Bound:
Lower Error Bound:
|
|
|
Trial 3:
Upper Error Bound:
Lower Error Bound:
|
|
Trial 4: (no time walk correction)
Upper Error Bound:
Lower Error Bound:
|
|
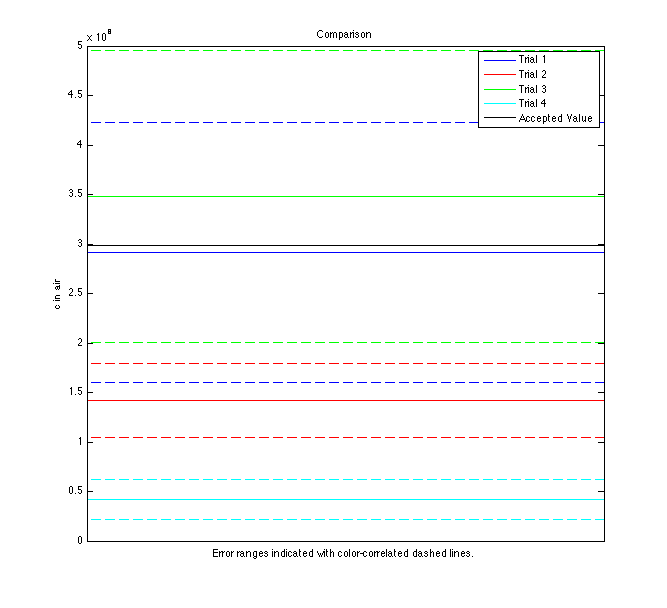
I notice that error range decreases with more measurements, but not necessarily accuracy. Here is a plot of all values with error compared to the accepted speed of light in air:
It appears that measurements taken over a large individual & total Δx, as in trials 1 & 3, yield the best results for c. Unfortunately, this experimental setup limits how much data can be taken this way, so the error is large. Small individual and total Δx yields an awful result, even though more data points narrowed the error range. The result of trial 4 illustrates how important adjusting for time walk is - c "walked" an entire order of magnitude! I wonder if taking data with small individual Δx over large total Δx would allow for the linear fit to filter out the "noise" from each small measurement in order to find the real trend of c. I believe the large amount of noise, from small x-stepping, combined with the small data range forced the trial 2 result far from its actual value.
This experiment and result illustrates the mechanics of accuracy of precision rather well, I think. Trial 2 is not accurate at all, but is much more precise than our more accurate measurements. I believe the lesson to take away from this is that narrowing error isn't the entire battle - what good does small error do when the physical value isn't inside error bounds?SJK 01:32, 1 November 2008 (EDT)

Good commentary. I think if you were to spend more time taking data as you suggest (large range, small intervals) and to do the uncertainty calculations correctly, you'd get a really great result for this lab!