User:Alexander T. J. Barron/Notebook/PHYC 307L Lab Notebook/speed of light notes
Speed of Light Lab
Set Up
Instrumentation
PMT: Perfection Mica Company N-134
Powering Up
Beginnng by powering the PMT at 1900 V. Power to LED: 190 V
At first we were unable to see any signal in the oscilloscope directly from either the PMT or the TAC. Then we moved our LED farther into the tube. We received our first signal peaking at about 1 V from the PMT.
We wanted to make sure that this signal was in fact due to the electric field of the light coming from the LED. And, in order to attain the best amplitude we rotated the PMT until its polarizer let in the greatest intensity.
After some adjustments were able to see a signal on the oscilloscope as such:
Directly from the PMT: 500-800 mV From the TAC: a square wave slightly delayed from the PMT signal at about 6 V
Data Trial
Oscilloscope:With ch 1 reading at 50mV and ch 2 reading at 500 mV with 250 ns divisions...
Data 1: Ch1 signal voltage: -192mV
Ch2 voltage: 4.92+- .08 V
Calibration
Instrumentation
PMT: Perfection Mica Company N-134
Powering Up
Beginnng by powering the PMT at 1900 V. Power to LED: 190 V
At first we were unable to see any signal in the oscilloscope directly from either the PMT or the TAC. Then we moved our LED farther into the tube. We received our first signal peaking at about 1 V from the PMT.
We wanted to make sure that this signal was in fact due to the electric field of the light coming from the LED. And, in order to attain the best amplitude we rotated the PMT until its polarizer let in the greatest intensity.
After some adjustments were able to see a signal on the oscilloscope as such:
Directly from the PMT: 500-800 mV From the TAC: a square wave slightly delayed from the PMT signal at about 6 V
Calibration Data
| Delay | Trial #1 | Trial #2 |
|---|---|---|
| 0 ns | 4.92 +/- .08 V | 4.90 +/- .08 V |
| 0.5 ns | 5.02 +/- .06 V | 4.98 +/- .1 V |
| 1.0 ns | 5.12 +/- .08 V | 5.04 +/- .08 V |
| 2.0 ns | 5.30 +/- .06 V | 5.28 +/- .12 V |
| 4.0 ns | 5.72 +/- .08 V | 5.72 +/- .1 V |
After consulting with Dr. Koch, we decided to not calibrate ourselves, instead using the TAC manual's calibration control settings:
10V = 50 ns
Brief Note on Experiment Anomaly
During the setup stage, we noticed that the output from the PMT was significantly altered whenever we connected or disconnected the TAC. This didn't seem to make sense, as I believe the signal measured directly from the PMT is on a totally different circuit from that routed through the TAC. We threw ideas around with Dr. Koch, discussing possible ground leakage/contamination and effects of electric field wavelengths vs. lengths of cable, but the discussion came up inconclusive. Terminating with a 50 Ω resistor at the oscilloscope killed the output entirely - I know so little about circuits other than basic DC stuff... we need an expert. Whatever effect this anomaly had didn't seem to throw the experiment out of whack, since our results came out pretty tasty.
Data
NOTE: ALL ΔX VALUES MEASURED FROM THE ENDPOINT OF THE PREVIOUS MEASUREMENT
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| All voltages measured with ± .02 V measurement error. |
Data Analysis
I can obtain Δt for each Δx with the TAC's calibration: [math]\displaystyle{ Δt = V_{meas} \times (5) 10^{-9} s }[/math]
The best estimate of the speed of light in air, cair, is the slope of the least-squares linear fit of the data, x vs. t.
I obtain error on cair through linear approximation:
Since cair depends on two measured values, x & t, with standard error σx, σt...
SJK 00:16, 1 November 2008 (EDT)

If you were calculating a final value by dividing a single x measurement by a t measurement, then this would be the correct error propagation formula. However, this isn't what you're doing! You're actually using linear regression. In linear regression, when assumptions are valid, you can calculate the maximum likelihood slope and intercept, along with uncertainties from the data (see week 8 lecture) or chapter 8 of Taylor). It's an exact formula which you could actually type by hand, but you can also use the built-in "LINEST" in excel, or whatever is available in Matlab. I did this in Excel for your data File:Speed of light, some of Justin, Der data.xls
Also, even using this formula, the way you're computing sigma_t and sigma_x does not make sense. The way you have it (if I'm reading matlab correctly) would mean that your uncertainty gets bigger and bigger the larger the range of data you take!
When you do it this way, you get an uncertainty of about 10% (3 cm / ns), much smaller than your way. You should really take a look at this, because the method you used is off-base.
[math]\displaystyle{ c_{air} = \frac{x}{t} \longrightarrow \sigma_{c_{air}} = \sqrt{(\frac{\partial c}{\partial t}|_{c_{best}} \sigma_t)^2 + (\frac{\partial c}{\partial x}|_{c_{best}} \sigma_x)^2} = \sqrt{(\frac{-x_{mean}}{t_{mean}^2} \sigma_t)^2 + (\frac{1}{t_{mean}} \sigma_x)^2} }[/math]
With this propagated error, I can tastefully display my best value along with its error bounds, [math]\displaystyle{ c_{air} \pm \sigma_{c_{air}} }[/math], as below:
NOTE: AXES ARE SET TO "TIGHT," SO SOME DATA POINTS ARE ON GRAPH EDGES
| Trial | Graphic Representation | Trial | Graphic Representation |
|
Trial 1:
Upper Error Bound:
Lower Error Bound:
|
|
Trial 2:
Upper Error Bound:
Lower Error Bound:
|
|
|
Trial 3:
Upper Error Bound:
Lower Error Bound:
|
|
Trial 4: (no time walk correction)
Upper Error Bound:
Lower Error Bound:
|
|
SJK 23:00, 31 October 2008 (EDT)

Actually, your y-intercept is completely arbitrary! You are only sensitive to time differences in this experiment, due to the unknown delays from the lengths of cable and other offsets. So, no reason to think it should go through (0,0)!
Unfortunately, I could not find any method for forcing the linear fit through the origin. Luckily for me, the y-intercept for all above plots is EXTREMELY close to the origin. I think this might be an indication of quality data taking, since a significant y-intercept would mean that the photons travel some distance in 0 time.
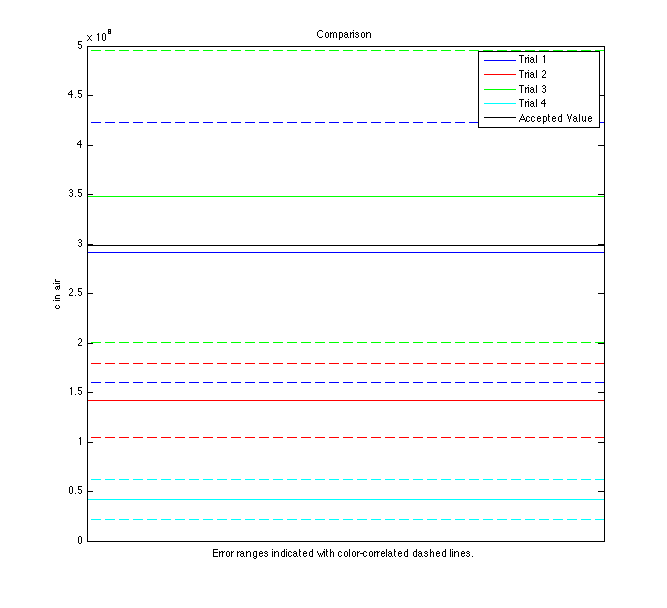
I notice that error range decreases with more measurements, but not necessarily accuracy. Here is a plot of all values with error compared to the accepted speed of light in air:
It appears that measurements taken over a large individual & total Δx, as in trials 1 & 3, yield the best results for c. Unfortunately, this experimental setup limits how much data can be taken this way, so the error is large. Small individual and total Δx yields an awful result, even though more data points narrowed the error range. The result of trial 4 illustrates how important adjusting for time walk is - c "walked" an entire order of magnitude! I wonder if taking data with small individual Δx over large total Δx would allow for the linear fit to filter out the "noise" from each small measurement in order to find the real trend of c. I believe the large amount of noise, from small x-stepping, combined with the small data range forced the trial 2 result far from its actual value.
This experiment and result illustrates the mechanics of accuracy of precision rather well, I think. Trial 2 is not accurate at all, but is much more precise than our more accurate measurements. I believe the lesson to take away from this is that narrowing error isn't the entire battle - what good does small error do when the physical value isn't inside error bounds?
Code
Used in MATLAB to obtain all above results, with appropriate lyrics:
SJK 23:46, 31 October 2008 (EDT)

It looks to me like you're "wasting" the first point in your analysis (by treating it as a special "initial" value). The first point (e.g., in trial 1, 0 cm, 2.62 V) should be included in the vectors and the fit. If you want, you can subtract 2.62 from all of them, but that's not necessary.
%% Speed of Light (not Ray of Light...Madonna....heh)
close all, clear all;
%% Trial 1 (And I Feel!)
Vvec1 = [2.54 2.40 2.06 1.82 1.66]; % Voltage info
Vvec1 = Vvec1 - 2.62;
xvec1 = [15 35 65 105 154]; % Distance info
xvec1 = xvec1./100;
Tvec1 = -Vvec1.*5.*10^-9; % Applying documented TAC calibration
fitcoeff1 = polyfit(Tvec1,xvec1,1) % Least-squares linear fit
t1 = linspace(Tvec1(1),Tvec1(end));
fit1 = polyval(fitcoeff1,t1);
scrsz = get(0,'ScreenSize');
figure('Position',[1 scrsz(4)/1.5 scrsz(3)/1.55 scrsz(4)/1.6]);
plot(Tvec1,xvec1,'ok');
hold on;
plot(t1,fit1,'k');
xlabel('t [s]');
ylabel('x [m]');
errT1 = std(Tvec1)/(length(Tvec1))^.5;
errx1 = std(xvec1)/(length(xvec1))^.5;
meanT1 = mean(Tvec1);
meanx1 = mean(xvec1);
errquad1 = ((errx1./meanT1).^2 + (errT1.*meanx1./(meanT1).^2).^2).^.5
bupper1 = fitcoeff1(1) + errquad1;
blower1 = fitcoeff1(1) - errquad1;
fitcoeff1upper = [bupper1 fitcoeff1(2)]
fitcoeff1lower = [blower1 fitcoeff1(2)]
fit1upper = polyval(fitcoeff1upper,t1);
fit1lower = polyval(fitcoeff1lower,t1);
hold on;
grid on;
axis tight;
plot(t1,fit1upper,'b--');
plot(t1,fit1lower,'r--');
legend('Trial 1 Data','Linear Fit','Upper Error Bound','Lower Error Bound','Location'...
,'NorthWest');
title('Trial 1')
%% Trial 2 (...Like I Just Got Home!)
Vvec2 = [7.74 7.56 7.42 7.52 7.40 7.32 7.24 7.50 7.18 7.26]; % Voltage info
Vvec2 = Vvec2 - 7.76;
xvec2 = [5 10 15 20 25 30 35 40 45 50]; % Distance info
xvec2 = xvec2./100;
Tvec2 = -Vvec2.*5.*10^-9; % Applying documented TAC calibration
fitcoeff2 = polyfit(Tvec2,xvec2,1) % Least-squares linear fit
t2 = linspace(min(Tvec2),max(Tvec2));
fit2 = polyval(fitcoeff2,t2);
scrsz = get(0,'ScreenSize');
figure('Position',[1 scrsz(4)/1.5 scrsz(3)/1.55 scrsz(4)/1.6]);
plot(Tvec2,xvec2,'ok');
hold on;
plot(t2,fit2,'k');
xlabel('t [s]');
ylabel('x [m]');
errT2 = std(Tvec2)/(length(Tvec2))^.5;
errx2 = std(xvec2)/(length(xvec2))^.5;
meanT2 = mean(Tvec2);
meanx2 = mean(xvec2);
errquad2 = ((errx2./meanT2).^2 + (errT2.*meanx2./(meanT2).^2).^2).^.5
bupper2 = fitcoeff2(1) + errquad2;
blower2 = fitcoeff2(1) - errquad2;
fitcoeff2upper = [bupper2 fitcoeff2(2)]
fitcoeff2lower = [blower2 fitcoeff2(2)]
fit2upper = polyval(fitcoeff2upper,t2);
fit2lower = polyval(fitcoeff2lower,t2);
hold on;
grid on;
axis tight;
plot(t2,fit2upper,'b--');
plot(t2,fit2lower,'r--');
legend('Trial 2 Data','Linear Fit','Upper Error Bound','Lower Error Bound','Location'...
,'NorthWest');
title('Trial 2')
%% Trial 3 (And I Feel!)
Vvec3 = [7.78 7.42 7.38 7.30 7.50 7.24]; % Voltage info
Vvec3 = Vvec3 - 7.80;
xvec3 = [25 50 75 100 125 150]; % Distance info
xvec3 = xvec3./100;
Tvec3 = -Vvec3.*5.*10^-9; % Applying documented TAC calibration
fitcoeff3 = polyfit(Tvec3,xvec3,1) % Least-squares linear fit
t3 = linspace(min(Tvec3),max(Tvec3));
fit3 = polyval(fitcoeff3,t3);
scrsz = get(0,'ScreenSize');
figure('Position',[1 scrsz(4)/1.5 scrsz(3)/1.55 scrsz(4)/1.6]);
plot(Tvec3,xvec3,'ok');
hold on;
plot(t3,fit3,'k');
xlabel('t [s]');
ylabel('x [m]');
errT3 = std(Tvec3)/(length(Tvec3))^.5;
errx3 = std(xvec3)/(length(xvec3))^.5;
meanT3 = mean(Tvec3);
meanx3 = mean(xvec3);
errquad3 = ((errx3./meanT3).^2 + (errT3.*meanx3./(meanT3).^2).^2).^.5
bupper3 = fitcoeff3(1) + errquad3;
blower3 = fitcoeff3(1) - errquad3;
fitcoeff3upper = [bupper3 fitcoeff3(2)]
fitcoeff3lower = [blower3 fitcoeff3(2)]
fit3upper = polyval(fitcoeff3upper,t3);
fit3lower = polyval(fitcoeff3lower,t3);
hold on;
grid on;
axis tight;
plot(t3,fit3upper,'b--');
plot(t3,fit3lower,'r--');
legend('Trial 3 Data','Linear Fit','Upper Error Bound','Lower Error Bound','Location'...
,'NorthWest');
title('Trial 3')
%% Trial 4 (...Quicker than a Ray of Light!)
Vvec4 = [6.30 5.84 5.32 4.74 4.50]; % Voltage info
Vvec4 = Vvec4 - 6.48;
xvec4 = [10 20 30 40 50]; % Distance info
xvec4 = xvec4./100;
Tvec4 = -Vvec4.*5.*10^-9; % Applying documented TAC calibration
fitcoeff4 = polyfit(Tvec4,xvec4,1) % Least-squares linear fit
t4 = linspace(min(Tvec4),max(Tvec4));
fit4 = polyval(fitcoeff4,t4);
scrsz = get(0,'ScreenSize');
figure('Position',[1 scrsz(4)/1.5 scrsz(3)/1.55 scrsz(4)/1.6]);
plot(Tvec4,xvec4,'ok');
hold on;
plot(t4,fit4,'k');
xlabel('t [s]');
ylabel('x [m]');
errT4 = std(Tvec4)/(length(Tvec4))^.5;
errx4 = std(xvec4)/(length(xvec4))^.5;
meanT4 = mean(Tvec4);
meanx4 = mean(xvec4);
errquad4 = ((errx4./meanT4).^2 + (errT4.*meanx4./(meanT4).^2).^2).^.5
bupper4 = fitcoeff4(1) + errquad4;
blower4 = fitcoeff4(1) - errquad4;
fitcoeff4upper = [bupper4 fitcoeff4(2)]
fitcoeff4lower = [blower4 fitcoeff4(2)]
fit4upper = polyval(fitcoeff4upper,t4);
fit4lower = polyval(fitcoeff4lower,t4);
hold on;
grid on;
axis tight;
plot(t4,fit4upper,'b--');
plot(t4,fit4lower,'r--');
legend('Trial 4 Data','Linear Fit','Upper Error Bound','Lower Error Bound','Location'...
,'NorthWest');
title('Trial 4')
%% Comparison (She's Got Herself a Universe)
trial1mean = ones(1,2).*fitcoeff1(1);
trial1up = ones(1,2).*bupper1;
trial1low = ones(1,2).*blower1;
trial2mean = ones(1,2).*fitcoeff2(1);
trial2up = ones(1,2).*bupper2;
trial2low = ones(1,2).*blower2;
trial3mean = ones(1,2).*fitcoeff3(1);
trial3up = ones(1,2).*bupper3;
trial3low = ones(1,2).*blower3;
trial4mean = ones(1,2).*fitcoeff4(1);
trial4up = ones(1,2).*bupper4;
trial4low = ones(1,2).*blower4;
real = ones(1,2).*2.981.*10^8;
compvec = [1 2];
figure('Position',[1 scrsz(4)/1.5 scrsz(3)/1.55 scrsz(4)/1.6]);
meanvec = {trial1mean,trial2mean,trial3mean,trial4mean};
upvec = {trial1up,trial2up,trial3up,trial4up};
lowvec = {trial1low,trial2low,trial3low,trial4low};
plot(compvec,meanvec{1},'b',compvec,meanvec{2},'r',compvec,meanvec{3},'g',compvec,...
meanvec{4},'c');
hold on;
plot(compvec,real,'k');
legend('Trial 1','Trial 2','Trial 3','Trial 4','Accepted Value');
plot(compvec,upvec{1},'--b',compvec,upvec{2},'--r',compvec,upvec{3},'--g',compvec,...
upvec{4},'--c');
plot(compvec,lowvec{1},'--b',compvec,lowvec{2},'--r',compvec,lowvec{3},'--g',...
compvec,lowvec{4},'--c');
title('Comparison');
SJK 01:23, 1 November 2008 (EDT)

I had to google these lyrics. I almost downloaded the MP3 from amazon. First time I've seen lyrics along with the matlab! I knew the song but hadn't realized it was about Junior Lab, so glad I learned that!