Nick Rohacz: Week 3
From OpenWetWare
Jump to navigationJump to search
Terminology
- Dynamical System - "A means of describing how one state develops into another state over the course of time." A set of equations that will be able to predict the changes in the state of a system. [[1]]
- Law of Mass Action - "A law stating that the intensity of a reaction is dependent on the degree of presence of the reactants responsible for the reaction." Simply, the kinetics of a reaction are dependent on the concentrations of reactants. [[2]]
- Homeostasis - " The ability of the body or a cell to seek and maintain a condition of equilibrium or stability within its internal environment when dealing with external changes." Basically, the tendency for a cell to maintain certain conditions that are optimal for necessary functions. [[3]]
- Equilibrium - "The condition in which all acting influences are balanced or canceled by equal opposing forces, resulting in a stable system." This is more of a state of balance that is achieved when outside forces are equal, not necessarily a tendency though. [[4]]
- Oscillation - "Fluctuation; variation; change back and forth." The motion, back and forth, of cell processes due to the presence or absence of molecules. [[5]]
- Autocatalysis - "A reaction in which one or more of the products formed acts to catalyze the reaction" Where one of the products being formed by the reaction, catalyzes its own reaction, therefore, producing more of itself. [[6]]
Apply the Law of Mass Action
- A + B → C
- A and B will produce C, but no backwards reaction
- k1 represents the forward rate constant, there is no backwards reaction.
- d[A]/dt = -k1[A][B]
- d[B]/dt = -k1[A][B]
- d[C]/dt = k1[A][B]
- A + B ↔ C
- A and B will produce C, C will also decompose into A and B
- k1 represents the forward rate constant, and k-1 is the backwards constant.
- d[A]/dt = k-1[C] - k1[A][B]
- d[B]/dt = k-1[C] - k1[A][B]
- d[C]/dt = k1[A][B] - k-1[C]
- A + B ↔ 2C
- 1 mole of A and B will produce 2 moles of C, however, it takes 2 moles of C to decompose into 1 mole of A and B.
- k1 represents the forward rate constant, and k-1 is the backwards constant.
- d[A]/dt = k-1[C]2 - k1[A][B]
- d[B]/dt = k-1[C]2 - k1[A][B]
- d[C]/dt = k1[A][B] - k-1[C]2
- 2A + 3B ↔ C+D
- 2 moles of A and 3 moles of B will produce 1 mole of both C and D, and backwards, 1 mole of both C and D will produce 2 moles of A and 3 moles of B.
- k1 represents the forward rate constant, and k-1 is the backwards constant.
- d[A]/dt = (k-1[C][D] - k1[A]2[B]3)1/2
- d[B]/dt = (k-1[C][D] - k1[A]2[B]3)1/3
- d[C]/dt = k1[A]2[B]3 - k-1[C][D]
- d[D]/dt = k1[A]2[B]3 - k-1[C][D]
Simulating Reaction Kinetics
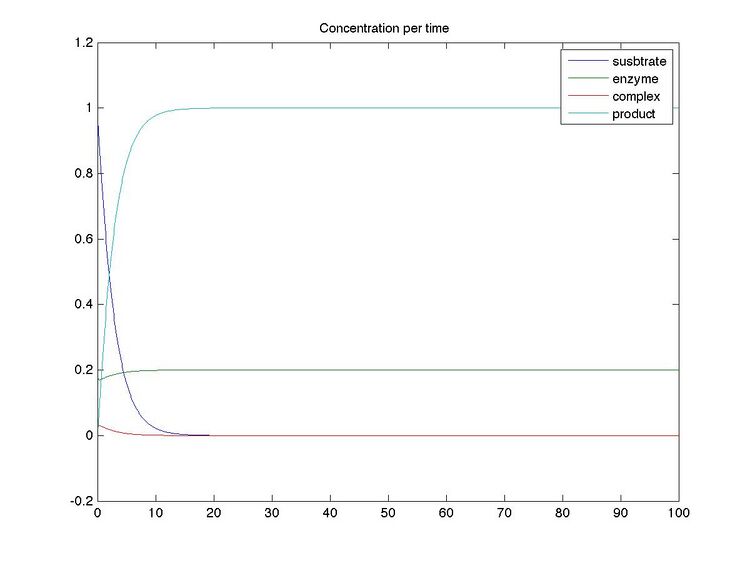
References
[Medical Dictionary] [Encyclopedia] [Mathworld]
Nicholas A. Rohacz 01:55, 31 January 2011 (EST)