Microfluidic Gradient Generators - Greg Schneider

Microfluidic Gradients Background

Simple microfluidic devices can allow for precise control over fluid mixing. Due to laminar flow, mixing in microfluidic devices is largely controlled by diffusion (see also Péclet number (Pe)) between different fluids at the interface. Microfluidic gradient devices can be precisely programmed to mix fluids by choosing how long two or more fluids contact one another and diffuse.^[1] Diffusion can be tuned by adjusting the respective flow rates of fluids, relative channel sizes and lengths, and the total contact area. Since gradients can now be generated in a stable and predictable manner it has opened up many avenues of research that were otherwise not possible. Gradient generation is useful for a broad range of fluid-related research applications, with biological applications being the most common.

Figure 1. A Corning 96-well Microtiter plate used for serial dilution/solution gradient preparation. By dosing each well with a different volume of diluent, a different concentration is achieved in each well. Microwell dosing is typically performed by a machine, which is less efficient than a microfluidic device would be. ^[6] Image by Wyatt Technology Corporation. ^[7]

Typically, equipment such as microtiter/microwell plate arrays with fluid wells have been used to create concentration gradients via serial dilution. A microwell plate is shown in Figure 1. Microfluidic gradient generators can significantly reduce preparation time compared to microwell plates, as well as the amount of liquid required to achieve similar results to microwell plates. Walker et al., compared the performance of a microfluidic gradient generator to a 96-well plate in the context of linear dilution. The microfluidic device used 100 times less fluid than the 96-well plate to achieve the same linearity. Furthermore, a microfluidic gradient generator can be used in a continuous fashion, and by changing flow rates the gradient concentrations can be changed in real time.^[2]

Mathematical Model

Slow diffusion at the liquid-liquid interface controls passive mixing within microfluidic devices, which is behavior occuring in the low Péclet number (Pe) region. Fick's law determines the overall mixing time for diffusive mixing. The mixing time [math]\displaystyle{ \mathrm\tau_{mix} }[/math] in a microfluidic channel is described by:

[math]\displaystyle{ \mathrm\tau_{mix} = \frac{d^2}{2D}\ }[/math]
Where:

• [math]\displaystyle{ \mathrm\tau_{mix} }[/math] is the mixing time
• d is the diffusive distance
• D is the diffusion coefficient

The mixing time influences channel length. For a given microfluidic device, the channel length must be adequate for the fluids in solution to mix completely. In gradient trees, for example, long channels are typically compacted into a small area for adequate mixing to occur in a small device.

Gradient Trees

Figure 2. A microfluidic gradient tree with 2 inlets and 7 outlets. All 7 outlets will result in a different concentration due to the variations in overall channel length and contact area between streams. Image by Dr. Sarah Perry.

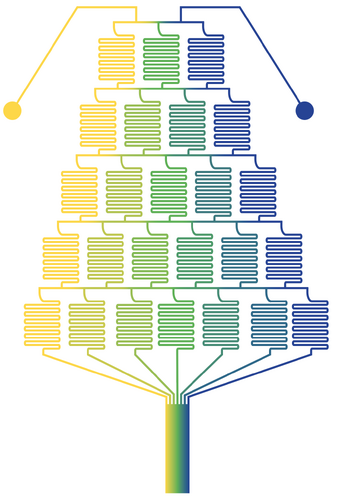
A gradient tree is a hierarchical microfluidic structure that can create highly complex and precise concentration gradients. The gradient resulting from a gradient tree is dependent on channel length, total contact area, and the number of contact areas.^[5] In Figure 2, the gradient tree features a multitude of winding channels. The channels are intended to be as long as necessary (described in the previously mentioned model) in a compact area to allow for the fluids to fully diffuse and mix completely before the next contact area is reached. Figure 2 represents a gradient tree which results in 7 linear dilutions based on 2 input streams. The leftmost outlet is a pure stream of the left inlet fluid. The rightmost outlet is a pure stream of the right inlet fluid. The center most outlet is an equal mixture of the right and left inlet fluids. Linearly formed concentration steps are formed in between. Each additional branch or layer added to the gradient tree introduces a new, step-wise change in the concentration between the two lines which come into contact in the horizontal "contact zone" channels. Linearity between each step can be maintained in this device by preserving equal volumetric flow rates between the two inlets.

Nonlinear Gradients

Gradients can be made to be nonlinear by creating situations in which mixing does not occur in linear steps. These steps can have various different patterns such as an exponential, logarithmic, or sigmoidal pattern. There are various microfluidic techniques to achieve this with the most common method involving varying fluid channel lengths or using asymmetrical channels. In a gradient tree, nonlinear gradients are formed using unequal flow rates of the inlet fluids. Microwell plate gradients are typically nonlinear, utilizing a nonlinear pattern. A microfluidic nonlinear gradient can be easily programmed for different types of nonlinearity.^[2] Channel width variation is considered more precise for forming nonlinear gradients, so equal flows can be maintained between inlets, and channel widths control the degree of non linearity. However, this requires more device planning and preparation.^[2]

Mathematical Model

After designing a device a reasonably accurate model the behavior of that device can be made before conducting actual tests. Based on the modeled behavior of the device, changes to the design or the parameters of the experiment can be adjusted. Simulations can be run in the x-y plane (2D) based off of the following governing equations:

Figure 3. Governing equations used to simulate nonlinear gradients.

Where:

• u⃗ is the velocity vector
• p is pressure
• ϕ is analyte concentration density
• Re is the Reynolds number
• Pe is the Péclet number

Equations 1 and 3 are continuity equations that can be used to solve steady-state Navier-Stokes equations. Equation 2 is the convection-diffusion equation that is used to determine the analyte concentration. In order to properly model a system, the specific device geometry, dimensions, and boundary conditions have to be taken into account. Evaluating concentration distributions are often aided by commercial solvers.^[2]

Methods For Creating Nonlinear Gradients

Varying Flowrates and Asymmetrical Geometry

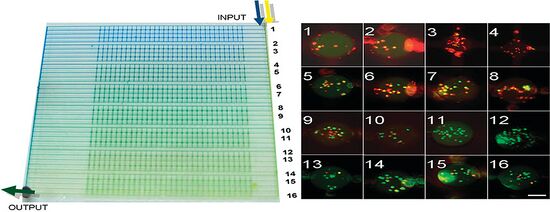
The geometry of a device can impact the concentration gradient a device produces. Asymmetry in a device can create a nonlinear gradient. In a device created by Selemovic et al. a grid of microfluidic channels are arranged in an asymmetric geometry with a coflow channel as an inlet at one end of the chip (Figure 4). The asymmetrical grid in their design allows for the partial mixing at each intersection or occur nonlinearly across the grid. Selemovic et al. were also able to change the type of concentration gradient based on the inlet flow rate. When using a relatively low flow rate an exponential concentration gradient was achieved and using high flow rates a sigmoidal concentration gradient would form.^[4]

Figure 4. A nonlinear gradient device created Selemovic et al.^[4] Reprinted with permission from Šeila Selimović, Woo Young Sim, Sang Bok Kim, Yun Ho Jang, Won Gu Lee, Masoud Khabiry, Hojae Bae, Sachin Jambovane, Jong Wook Hong, and Ali Khademhosseini Analytical Chemistry 2011 83 (6), 2020-2028 DOI: 10.1021/ac2001737 . Copyright 2011 American Chemical Society.

Modified Gradient Tree with Varying Horizontal Channel Width

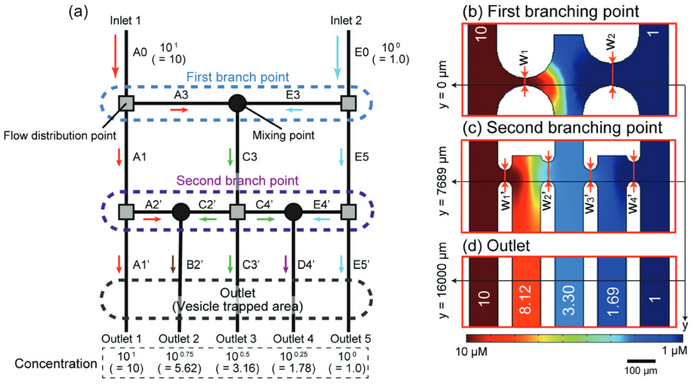
In a study by Abe et al., a microfluidic device resembling a tree like structure was created to produce a nonlinear, logarithmic concentration gradient. In their device the channels were divided at every branch with mixing points along each branch as depicted in Figure 5. The horizontal channels in between each of the mixing and dividing points were varied. Abe et al. found that by varying the horizontal channel width they were able to shorten their overall channel lengths to 1/7th of that of a standard nonlinear concentration device.^[2]

Figure 5. Device made by Abe et al. which creates a nonlinear gradient by varying the horizontal channel widths. (a)Schematic of the chip (b)Concentrations at the chip branching points and outlet.^[2]Reprinted with permission from Abe, Y., Kamiya, K., Osaki, T., Sasaki, H., Kawano, R., Mikia, N., Takeuchi, S. Nonlinear concentration gradients regulated by the width of channels for observation of half maximal inhibitory concentration (IC50) of transporter protein. Royal Society of Chemistry. 2015,140. DOI:10.1039/C4AN02201G. Copyright 2015Royal Society of Chemistry.

Induced Charge Electro-Osmosis (ICEO)

Applying electric fields to a linear gradient producing device can cause the gradient to form nonlinear patterns. Jain et al. created a nonlinear gradient by introducing a conductive obstacle in the channel of linear gradient producing device. By applying an electric field to this device, they were able to utilize induced charge electro-osmosis (ICEO) to create a nonlinear gradient field. Induced charge electro-osmosis is when you have fluid flow or particle motion that are electrically driven by the movement of positive and negative ions which drags some of the surrounding fluid with it. The ICEO causes transverse convection which results in a nonlinear and asymmetrical gradient. Jain et al. were able to switch between linear and nonlinear gradient by altering the applied electric field.^[10]

Uses

Gradient trees are regularly used in biological studies. Gradients are useful in studying biology because many aspects of nature and our environment are heterogeneous in nature, so studying many aspects of biology in a homogeneous setting is not always useful. In our environment, these heterogeneous aspects often display itself in gradients, such as when examining aspects of evolution in biology.^[8] Microfluidic gradient generators can help mimic these gradient conditions we see in nature when conducting studies. Depending on the type of gradient that is needed a linear or nonlinear gradient device might be used, as some gradients observed in biology are not linear.

Walker et al., proposed the use of a linear microfluidic gradient generator to perform cytotoxicity studies.^[3] In the case of cytotoxicity studies, these miniaturized studies reduced cell waste and reagent use. After creating a desirable gradient profile, the authors were able to dose each gradient outlet with various treatments in a precise manner with continuous flow. Materials are a further advantage for microfluidic devices in this type of study. Since microfluidic devices are often made of optically transparent materials such as glass or PDMS, Walker et al., were able to record data in situ using florescence.^[3]

Another example of gradient application is in drug resistance research; microfluidic devices were used to form concentration gradients of antimalarial drugs to test their efficacy across a range of concentrations. In the case of Rhomphosri et al., a linear gradient generation device was used in this study to create gradient of antimalarial drug gradient and exposed in to malaria to observe antibiotic resistance evolution. Rhomphosri et al. also observed antibiotic resistance in a homogeneous, high resistance environment and found that the time to get high resistance strains was actually shorter in the environment with a drug concentration gradient.^[8]

Nonlinear gradient generation devices are particularly useful for biological applications as well. For example, studying chemotaxis. A nonlinear microfluidic gradient which flows continuously can show how a cell responds to a gradient changing through time as well as how shear stress (i.e., changes in the flow behavior) influences cell motility. Being able to study cell motility in continuous, temporally varying conditions more closely mimics real biological systems. Nonlinear gradients based on flow rate changes are often used for chemotaxis studies on cancer cells. ^[3]

References

1. Gao, Y., Sun, J., Lin, W., Webb, J., Li, D. A compact microfluidic gradient generator using passive pumping. Microfludics and Nanofluidics. 2012, 12. DOI: https://doi.org/10.1007/s10404-011-0908-0

2. Abe, Y., Kamiya, K., Osaki, T., Sasaki, H., Kawano, R., Mikia, N., Takeuchi, S. Nonlinear concentration gradients regulated by the width of channels for observation of half maximal inhibitory concentration (IC50) of transporter protein. Royal Society of Chemistry. 2015,140. DOI: https://doi.org/10.1039/C4AN02201G

3. Walker, G., Monteiro, N., Rouse, J., O'Neill, A. A linear dilution microfluidic device for cytotoxicity assays. Lab on a Chip. 2006, 7. DOI: https://doi.org/10.1039/b608990a

4. Selimovic, S., Sim, W., Sang Bok Kim, Yun Ho Jang, Won Gu Lee, Masoud Khabiry, Hojae Bae, Sachin Jambovane, Jong Wook Hong, Ali Khademhosseini. Generating Nonlinear Concentration Gradients in Microfluidic Devices for Cell Studies. Analytical Chemistry. 2020, 83. DOI: https://doi.org/10.1021/ac2001737

5. Wang, Y.-H., Ping, C.-H., Sun, Y.-S. Design of Christmas-Tree-like Microfluidic Gradient Generators for Cell-Based Studies. Chemosensors. 2023, 11. DOI: https://doi.org/10.3390/chemosensors11010002

6. Shen, Q., Zhou, Q., Lu, Z., Zhang, N. Generation of Linear and Parabolic Concentration Gradients by Using a Christmas Tree-Shaped Microfluidic Network. Wuhan University Journal of Natural Sciences. 2018, 23. DOI: https://doi.org/10.1007/s11859-018-1317-y

7. Corning 96 Well Plate. Wyatt Technology Corporation. Product number P8802-09602. https://store.wyatt.com/shop/plate-reader/wpr3/corning-96-well-plate/

8. Rhomphosri, S., Changruenngam, S., Chookajorn, T., Modchang, C. Role of a Concentration Gradient in Malaria Drug Resistance Evolution: A Combined within- and between-Hosts Modelling Approach. Scientific Reports. 2020, 10. DOI: https://doi.org/10.1038/s41598-020-63283-2

9. Perry, S.L. ChE 535, Lecture 04, Fluid Flow and Mixing. UMass Amherst Department of Chemical Engineering. 2023.

10. Jain, M., Yeung, A., Nandakumar, K. (2010). Induced charge electro-osmotic concentration gradient generator. Biomicrofluidics, 4(1), 014110. DOI: https://doi.org/10.1063/1.3368991