Inertial Focusing - Nick O'Hare
Introduction
In microfluidics, particles in a solution can often range from 10s of nanometers, to 10s of micrometers. The large variability in particle size, shape, density, etc. makes it necessary to produce devices which effectively separate them. There are two major branches of technologies for separation in microfluidics, active and passive. Active technologies include magnetophoresis, dielectrophoresis, and optical tweezers [1]. Active methods apply an external force on the fluid, and provide more control over separation despite being slow and often energy intensive. Passive technologies on the other hand rely solely on the geometry of the microfluidic channel for separation. In the past decade, the passive technique of inertial focusing has gained considerable attention in the scientific community for its cost effectiveness, precise control, and high flow velocities [4].
Inertial focusing is a process where randomly distributed particles entering a channel will migrate perpendicularly to measurable equilibrium positions after a long enough distance. In the past, most researchers believed that microfluidic devices should operate under laminar flow as well as Stokes flow to be useful so the particles flow in highly predictable streamlines. Additionally, in Stokes flow, inertial forces are small compared to viscous forces, so calculations of force are easier to perform [3]. However, researchers have discovered that operating flow while still in the laminar regime, but where inertial effects can no longer be ignored (1<Re>100), particles in microfluidic channels can be sorted, separated, mixed, etc. in a controlled manner [1]. Inertial focusing can only be observed in micro channels since a high velocity gradient is required. This page will explore the forces involved, as well as the technologies at the forefront in the field of microfluidics taking advantage of inertial focusing.
Dynamics
Shear Gradient Lift Force and Wall Induced Lift Force
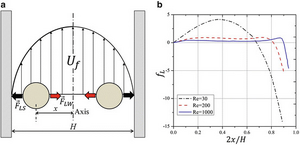
Within a channel, a typical velocity profile is parabolic where velocity is at a maximum in the middle of the channel, and decreases as the fluid approaches the wall. Thus, each particle in the fluid experiences a different velocity on each side of it [4]. To offset this varying velocity, the fluid surrounding the particle must produce a force on the side of the particle with the greater velocity. This will create a shear gradient and cause the particle to move towards the wall, which is the area with the lowest difference in velocity [5]. A higher Reynolds number will increase this lift force.
Wall induced lift force counteracts the shear gradient lift force by pushing the particle towards the center of the channel. The constricted fluid between the wall and the particle will produce a higher pressure, resulting in a pressure gradient. Since the particle would like to move from high pressure to low pressure, it migrates perpendicular to the wall, towards the center of the channel. The shear gradient lift force and the wall induced lift force balance each other out, and result in an equilibrium position for the particle. This equilibrium position will be different depending on the properties of each particle, which is the basis of inertial focusing [5].
Dean Flow Drag Force

Dean flow is characterized by a change in motion of the particle caused by a curvature modification along the channel. This curvature change produces a pressure gradient where the velocity is greater on the outside of the channel. The pressure difference causes secondary flow, known as Dean vortices, since the main direction of the flow changes [6]. This secondary flow enacts a drag force on the particle, pushing it towards the outside of the channel. Inertial focusing often utilizes Dean flow drag force because often times the difference in equilibrium positions created by the balance of the wall lift force and the shear gradient lift force of different sized particles is not substantial enough to effectively separate them. The Dean force scales proportionally with diameter squared, meaning larger particles experience a greater Dean force, pushing them further to the outside of the channel [5].
Property Considerations
Particle Properties
Inertially focused devices are well suited for biological purposes since the density of the particle is often similar to the fluid it is suspended in. This is ideal since a centrifugal force can be ignored. An example of this would be the separation of red blood cells, white blood cells, and MCF-7 cancer cells (~1000 kg/m^3) from the plasma it is suspended in (~1025 kg/m^3) [7] . However, if the inertially focused device was used to separate particles with a much greater density than the fluid (eg. water filtration), then a centrifugal force would have to be taken into account which will effect the equilibrium position and complicate math models [5].
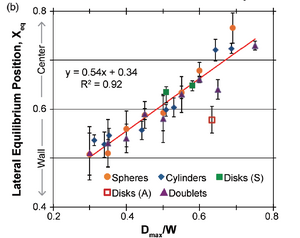
Another key particle property consideration is the shape of the particle. Equilibrium positions of a particle are only affected by a particle's maximum diameter, meaning a non-spherical particle with a maximum diameter of X will have about the same equilibrium position of a spherical particle with a maximum diameter X [8]. This property allows for inertially focused devices to be extremely useful for separating irregularly shaped particles (cells) and particles with large surface areas designed to maximize chemical reactions [8]
Fluid Properties
The most essential fluid property consideration is the ratio of particles to fluid. The maximum limit of percent particles to solution is estimated to be "1%-3%" [5]. Past this threshold of particle concentration, inertial focusing will begin to break down due to particle-particle interactions. It has also been shown that a high particle concentration can shift equilibrium positions towards the outside of a channel [5].

Another fascinating fluid application is the introduction of a polymer to the solution. As long as the polymer does not compromise the particle, in some situations it is useful to add a polymer to enact a viscoelastic force [9]. This viscoelastic force can balance with the Dean drag force since the drag force is moving the particle towards the outside of the channel and the viscoelastic force centers the particle. This can be a desired effect to further separate the equilibrium positions of the differently sized particles [9].
Channel Design
Channel Length
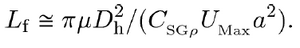
Particles must migrate a certain length in a channel in order to equilibrate to their final positions. This length equation has been theorized by Di Carlo using "the balance of the shear gradient lift force and Stokes drag force" [2] . This equation intends to aid in the design of an inertially focused device but is not precise due to the complexity of the force balance.
Cross Section
There are several different cross section shapes used in the field of inertial focusing. However, The two most common shapes are a square and circle. In a square channel, randomly sorted particles will migrate to four equilibrium positions near the center of each face wall based on the balance of the wall lift force and shear gradient force [1]. In the case of circular channels, an annulus of equilibrium positions occurs. A recent area of study using trapezoidal cross sectional areas has shown an increase in separation of differently sized particles compared to square and circular channels. This is seemingly due to an increase in the Dean flow velocity gradient for trapezoids [5]. The most significant difference between differently shaped cross sections is that inertial forces will be stronger for smaller dimension cross sections, resulting in focusing occurring sooner.
Straight Channels
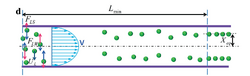
In general, Straight channels are simpler because there is no secondary forces to consider based on the geometry of the channel. The equilibrium positions are solely based on the balance of the wall lift force and shear gradient lift force making straight channels ideal for observing the concept of inertial focusing [4]. However, they are limited since they usually require very long channel lengths and lack the advantage of separating equilibrium positions by a factor of particle diameter squared as observed in Dean flow. However, straight channels have proven to be useful for applications like sheathless alignment and 5 µm and 15 µm beads [10].

Spiral Channels Spiral geometries are often used when taking advantage of Dean flow because of their constant curvature, allowing for easier manipulation of the particles [5]. As stated above, introducing curvature to a channel will create a secondary flow known as Dean flow that is going to cause the particle to move perpendicularly in the channel. Dean flow and the shear gradient lift force are opposing forces on the inner channel, causing a new equilibrium position to rise for each sized particle [11]. These types of devices are particularly useful for the separation of cancer cells, red and white blood cells, and for more closely sized particles than straight channels [4].
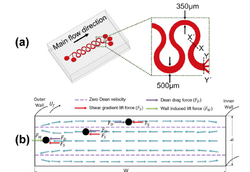
Asymmetric Channels
Asymmetrically curved channels utilize a similar secondary flow force as spiral channels in order to further separate particles. However, since they do not have a constant curvature, the Dean number is not constant [12]. This difference is an advantage as well as a disadvantage because it allows for optimal separation depending on the Dean number, but makes calculations far more complex [5]. Asymmetrical sorting is best suited to processes where precise enrichment is critical.
Applications
Particle Separation
The most obvious application for these inertially focused devices is for micro-particle separation. There are two general strategies for this: Isolating one particle of particular interest and sorting out the rest or having multiple channels each aimed at collecting a particular particle. An example of isolating one particle is using an inertially focusing device to sort out bacteria from blood [13]. Mach et al. used a 40 micro-channel with a gradually increasing expansion and collection region in order to manipulate equilibrium positions. The device was found to be able to remove >80% of bacteria with a throughput of 400 cells/min. It is hoped that this device can be used to separate several different cells from large volume samples [13].
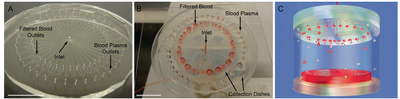
Another application is using a spiral sorting device in order to separate different sized cancer spheroids by size. Drug screening micro-chips require similarly sized spheroids since diffusivity of the drug plays such a large role in efficacy. Preferentially sorting the spheroids into individual channels using a continuously sorting inertially focused device could make this process much less labor intensive.
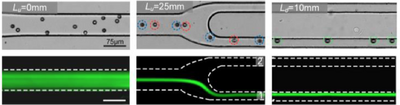
Sheathless Alignment
Many biological measurements like flow cytometry require the precise alignment and order of particles to properly function. Traditionally, this requires a sheath flow in order to space out particles [5]. However, Wang et al. have used a straight channel inertially focusing device to space out particles into a single ordered stream for the use in flow cytometry without the need for sheath flow [10]. If the process can become more efficient and streamlined, it could eliminate the need for sheath flows.
Volume Reduction Often times a more particle-enriched solution is desired when performing a particular experiment. A conventional way of reducing the amount of fluid would be to run the sample through a centrifuge and then drawing off the liquid that rises to the top. However, an inertially focusing device could create two streams: A particle enriched stream and particle deficient stream. A process that could continuously provide an enriched stream would theoretically save time and money.
Future Prospects
Inertial focusing is a promising field for its high throughput, low cost, and time saving capabilities. Nonetheless, there are some major hurdles that still must be overcome by researchers. The main issue is that even though increasing the inertial forces until particles begin to sort into predictable streamlines works in theory, the number of potential forces and complexity still makes it difficult to predict exact positions. For this reason, math models still far outperform the actual experimental results. Another problem that was mentioned in the fluid properties section is the upper limit of particle to fluid fraction. Solutions with very high particle density will not focus correctly unless a different model is created.
Regardless, the field of inertial focusing has been growing exponentially in the past decade because of its seemingly endless applications in the biomedical field [13]. With further research, these devices have the potential to be essential lab technologies in the coming years.
[1] Amini, H., Lee, W., & Carlo, D. D. (2014). Inertial microfluidic physics. Lab on a Chip, 14(15), 2739–2761.
[2] Di Carlo, D., Irimia, D., Tompkins, R. G., & Toner, M. (2007). Continuous inertial focusing, ordering, and separation of particles in microchannels. Proceedings of the National Academy of Sciences of the United States of America, 104(48), 18892–18897.
[3] Gou, Y., Jia, Y., Wang, P., & Sun, C. (2018). Progress of Inertial Microfluidics in Principle and Application. Sensors (Basel, Switzerland), 18(6).
[4] Zhang, J., Yan, S., Yuan, D., Alici, G., Nguyen, N.-T., Warkiani, M. E., & Li, W. (2015). Fundamentals and applications of inertial microfluidics: a review. Lab on a Chip, 16(1), 10–34.
[5] Martel, J. M., & Toner, M. (2014). Inertial Focusing in Microfluidics. Annual Review of Biomedical Engineering, 16, 371–396.
[6] Nivedita, N., Ligrani, P., & Papautsky, I. (2017). Dean Flow Dynamics in Low-Aspect Ratio Spiral Microchannels. Scientific Reports, 7, 44072.
[7] Abdulla, A., Liu, W., Gholamipour-Shirazi, A., Sun, J., & Ding, X. (2018). High-Throughput Isolation of Circulating Tumor Cells Using Cascaded Inertial Focusing Microfluidic Channel. Analytical Chemistry, 90(7), 4397–4405.
[8] Hur, S. C., Choi, S.-E., Kwon, S., & Carlo, D. D. (2011). Inertial focusing of non-spherical microparticles. Applied Physics Letters, 99(4), 044101.
[9] Lee, D. J., Brenner, H., Youn, J. R., & Song, Y. S. (2013). Multiplex Particle Focusing via Hydrodynamic Force in Viscoelastic Fluids. Scientific Reports, 3.
[10] Wang, X., Zandi, M., Ho, C.-C., Kaval, N., & Papautsky, I. (2015). Single stream inertial focusing in a straight microchannel. Lab on a Chip, 15(8), 1812–1821.
[11] Hasni, A. E., Göbbels, K., Thiebes, A. L., Bräunig, P., Mokwa, W., & Schnakenberg, U. (2011). Focusing and Sorting of Particles in Spiral Microfluidic Channels. Procedia Engineering, 25, 1197–1200.
[12] Özbey, A., Karimzadehkhouei, M., Alijani, H., & Koşar, A. (2018). Microparticle Inertial Focusing in an Asymmetric Curved Microchannel. Fluids, 3(3), 57.
[13] Mach, A. J., & Carlo, D. D. (2010). Continuous scalable blood filtration device using inertial microfluidics. Biotechnology and Bioengineering, 107(2), 302–311.
