IGEM:IMPERIAL/2008/Bioprinter/MotilityModel
Modelling Bacteria Motility
The key question here is, how can we quantify bacteria motility? We know that we are able to vary light intensity and wavelength along the visible spectrum, thus we can turn on and off the clutch mechanism described in the previous section.
The following paper describes the quantification of random motility using individual cell and population scale assays [1].
In a homogenous solution, the random motility coefficient is given by:
where [math]\displaystyle{ \mu_o\, }[/math] is the random motility coefficient, [math]\displaystyle{ \nu\, }[/math] is the mean cell swimming speed, [math]\displaystyle{ \tau\, }[/math] is the mean run time and [math]\displaystyle{ \theta\, }[/math] is the turn angle. Under the influence of a chemical gradient, the chemotactic motion is given by:
where [math]\displaystyle{ \nu\, }[/math] is the individual cell swimming speed, [math]\displaystyle{ a }[/math] is the attractant concentration and its gradient [math]\displaystyle{ \frac{\delta\,a}{\delta\,x} }[/math], [math]\displaystyle{ K_d }[/math] is the attractant-receptor dissociation constant, and [math]\displaystyle{ \chi_o\, }[/math] is the chemotactic sensitivity coefficient. [math]\displaystyle{ \chi_o\, }[/math] represents the fractional change in cell dispersal capability per unit of fractional change in receptor occupancy.
Flagella Motor
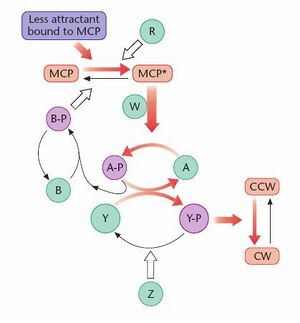
The flagellum motor spins at a frequency in the order of 100Hz. Counter-clockwise (CCW) rotation causes the bacteria to exhibit steady motion i.e. "running", whereas Clockwise (CW) rotation causes a change in direction i.e. "tumbling". During CCW rotation, the bacteria swim steadily in a direction parallel to its long axis for approximately 1s, followed by tumbling for a fraction of a second, and then reverting back to swimming [4].
At top speed, all flagella filaments forms a bundle and spins CCW, propelling the bacteria forward. Tumbling is initiated when the bundle flies apart, and one or more flagella spins CW. The switch between CCW and CW rotation is random, and is regulated by chemoattractants and chemorepellants, meadiating chemotaxis. The protein which directly interacts with the motor machinery is CheY. CheY-P binds to the cytoplasmic face of the flagella motor, causing an increased probability of CW rotation by reducing the free energy of the CW state relative to the CCW state. The phosphorylation of CheY is regulated by chemoattractant and chemorepellant molecules.
The flagella motor is powered by the proton motive force Δp. Δp is a function of the transmembrane potential and the difference in intra and extracellular pH: [math]\displaystyle{ \Delta\,p = \frac {kT}{e} ln (\frac{C_1}{C_2}) + V_m }[/math] where [math]\displaystyle{ k }[/math] is the Boltzmann's constant, [math]\displaystyle{ T }[/math] is the absolute temperature, [math]\displaystyle{ e }[/math] is the electronic charge of a proton, [math]\displaystyle{ C_1 }[/math] and [math]\displaystyle{ C_2 }[/math] are the internal and external [math]\displaystyle{ H^+ }[/math]concentrations espectively, and [math]\displaystyle{ V_m }[/math] is the transmembrane potential.
Flagellum development
During growth of B subtilis, in the mid exponential phase there exist 2 types of cells. One population with sigma factor D being turned ON, allowing the expression of the flagellum and permitting motility and undergoing cell division. The other population has sigma factor D switched OFF, the cells grow as long non-motile chains. The gene SwrA causes the sigma factor D to turn ON, and so expression of flagellum biosynthesis. Another gene SwrB downstream of SwrA, favours sigmaD directed expression as well. [5]
B subtilis swarms on a solid surface and swims in liquid. Lab strains are not able to swarm due to their inability to produce surfactant. However, we should choose a medium that would allow the cells to swim.
Motility Analysis Methods
- This paper describes a method using a Camera to study the motility.[6]
- Three-Dimensional Tracking Microscope
The tracking microscope developed by Berg (1971) recrods 3D movement of motile bacteria. The position of each cell is sampled at pre-determined time interval. Analysis of x,y and z coordinates of each cell is carried out using the algorithm of Berg and Brown (1974). Parameters of interest are swimming speed [math]\displaystyle{ \nu\, }[/math], run time [math]\displaystyle{ \tau\, }[/math] and turn-angle distribution [math]\displaystyle{ \theta\, }[/math]. Using these parameters, the random motility coefficient [math]\displaystyle{ \mu_o\, }[/math] can be calculated.
- Stopped-Flow Diffusion Chamber (SFDC)
The SFDC is a bacterial-transport assay that uses impinging flow to generate a step-change initial condition between two bacterial solutions differing only in their stimulus concentrations. For random motility experiments, a dual-syringe pump is used to pump dilute bacterial suspension through the top valve of the SFDC and random motility buffer through the bottom valve. The impinging flow exits the SFDC through the side valves, resulting in a step-change between the bacteria and buffer solution.
- Capillary Assay
A capillary filled with motility buffer or chemoattractant is inserted into a dilute bacterial suspension. The accumulation of bacteria at the mouth and within the capillary is then quantified. The random motility coefficient can then be determined by knwon equations.
References
- Lewus P and Ford RM. Quantification of random motility and chemotaxis bacterial transport coefficients using individual-cell and population-scale assays. Biotechnol Bioeng. 2001 Nov 5;75(3):292-304. DOI:10.1002/bit.10021 |
- Lovely PS and Dahlquist FW. Statistical measures of bacterial motility and chemotaxis. J Theor Biol. 1975 Apr;50(2):477-96. DOI:10.1016/0022-5193(75)90094-6 |
-
Perturbation Expansion of Alt's Cell Balance Equations Reduces to Segel's One-Dimensional Equations for Shallow Chemoattractant Gradients. Kevin C. Chen, Roseanne M. Ford, Peter T. Cummings. SIAM Journal on Applied Mathematics, Vol. 59, No. 1, (Sep. - Oct., 1998), pp. 35-57[1]
- Berg HC. The rotary motor of bacterial flagella. Annu Rev Biochem. 2003;72:19-54. DOI:10.1146/annurev.biochem.72.121801.161737 |
- Kearns DB and Losick R. Cell population heterogeneity during growth of Bacillus subtilis. Genes Dev. 2005 Dec 15;19(24):3083-94. DOI:10.1101/gad.1373905 |
- Mendelson NH, Bourque A, Wilkening K, Anderson KR, and Watkins JC. Organized cell swimming motions in Bacillus subtilis colonies: patterns of short-lived whirls and jets. J Bacteriol. 1999 Jan;181(2):600-9. DOI:10.1128/JB.181.2.600-609.1999 |