Falghane Week 14/15

Purpose

The purpose of this assignment was to model the chemostat used in Tai et al. (2007) using MATLAB.

Methods

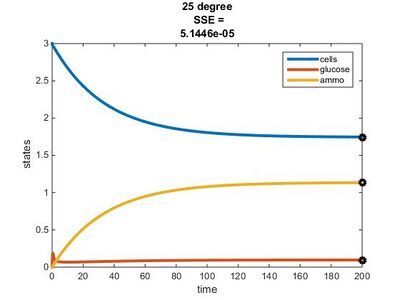
1. Use the Arrhenius equation (rate = A*exp(-B/(R*T)) to model the temperature dependence of the chemostat reaction.

• Ea was found from the slope between ln(k) and 1/temp (K) and finding B which equaled Ea.​
• Equation: A = k/ e^-(Ea/RT) was then used to solve for A​
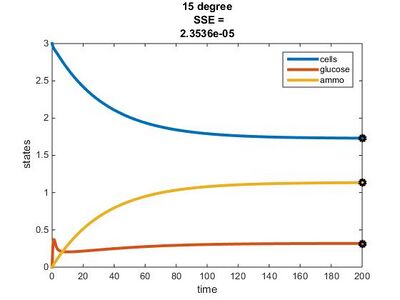
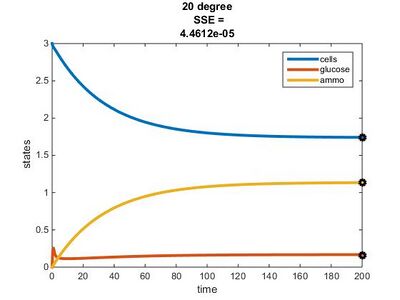
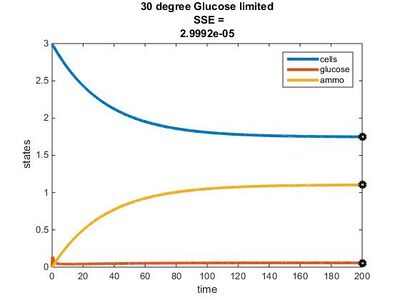
• Then Arrhenius Equation: rate = A*exp(-B/(R*T ) was used to find rates at temperatures 15, 20, 25 in Kalvin. ​
• Then the New Rates were added to MATLAB to model temperature dependence of the chemostat reaction​

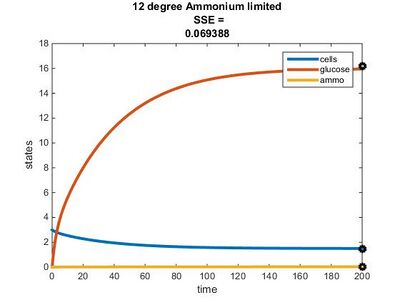
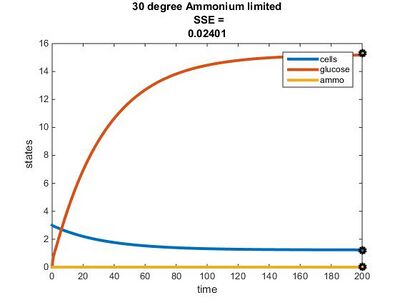
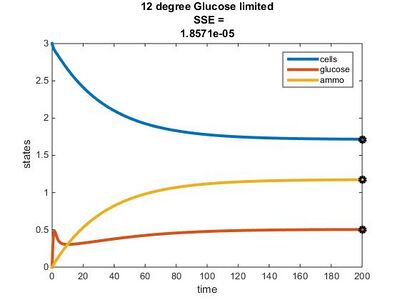
2. Investigating the glucose efficiency/ waste constant

• The values of E for glucose-limited and ammonium-limited conditions were noted.
• For each temperature (12, 30), the function E(y) that matches the two points of (y,E) data was found.
• The chemostat_2nutrient_dynamics.m file was modified to use the functions created.
• The resulting simulation was compared to the previous one.

Results

• Determing the A & B constants:
  • B found to be 69,840.59 from B = (Rln(k1/k2))/(1/T1-1/T2).
  • A found to be 4.979 * 10^11 from A = k/ e^-(Ea/RT).

• Rate values:
  • r(15°C) = (4.979 x 10^11)e^(-69840.59)/((8.314)(288.15)) = 0.1087
  • r(20°C) = (4.979 x 10^11)e^(-69840.59)/((8.314)(293.15)) = 0.1787
  • r(25°C) = (4.979 x 10^11)e^(-69840.59)/((8.314)(298.15)) = 0.289

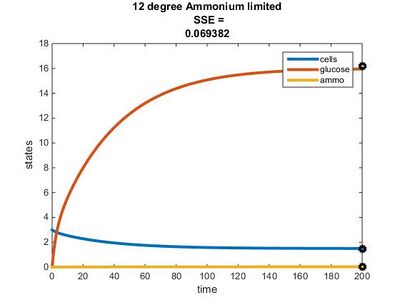
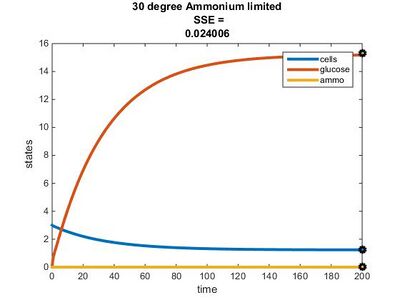
• Efficiency constant Investigation
  • Original: E = 1/Y New equation: where E = my + b
  • y = residual glucose
  • point intercept m = (y-y)/(x-x) was used to determine m and thenew value was plugged into E = my + b to determine b
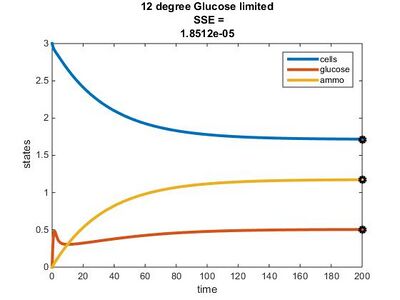
  • 12°C: E = 0.363y + 14.11
  • m = (14.3-20)/(0.5045-16.22) = 0.363
  • b=14.11
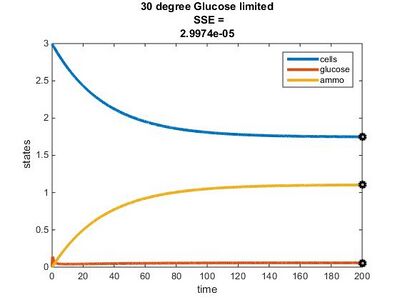
  • 30°C: E = 0.7y + 14.25
  • m = (14.3-25)/(.0541-15.33) = 0.7
  • b=14.25

Temperature Dependence Graphs

Efficiency Constant Graphs

Original Model

New Model

Acknowledgments

• I worked with my homework partner, Edward Ryan R. Talatala to complete this assignment.
• I also worked with Austin to work on the efficiency constant investigation.

References

• Tai, S. L., Daran-Lapujade, P., Walsh, M. C., Pronk, J. T., & Daran, J. M. (2007). Acclimation of Saccharomyces cerevisiae to low temperature: a chemostat-based transcriptome analysis. Molecular Biology of the Cell, 18(12), 5100-5112. DOI: 10.1091/mbc.e07-02-0131

• Dahlquist, K. and Fitzpatrick, B. (2019). BIOL388/S19:Week 14/15. [online] openwetware.org. Available at:Week 14/15 Assignment Page [Accessed May 8 2019].

• Tai, S. L., Boer, V. M., Daran-Lapujade, P., Walsh, M. C., de Winde, J. H., Daran, J. M., and Pronk, J. T. (2005). Two-dimensional transcriptome analysis in chemostat cultures: combinatorial effects of oxygen availability and macro- nutrient limitation in Saccharomyces cerevisiae. J. Biol. Chem. 280, 437–447.