Drummond:Viability
Introduction
Problem: Create a model to illustrate the mechanisms by which the addition of paromomycin leads to cell growth inhibition
Two extreme models of cell growth inhibition were proposed: the first, pertaining to the survival of cells, the second, involving the speed at which cells are born. The first model hypothesizes that, for every cell doubling, some fraction of the offspring (a "survival" rate) live while the rest are dead. The doubling time of the live cells in this model is unaffected. The second model hypothesizes that 100% of the offspring survive, but the doubling time of these cells is increased by some factor.
Model
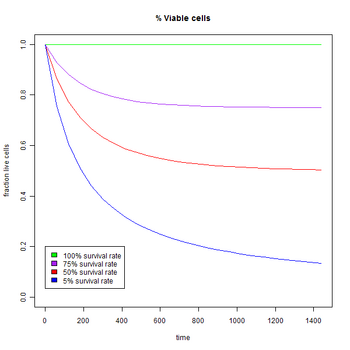
For this model, we will consider the doubling time of a cell (td to be the amount of time required for any number of cells to be doubled. Unlike a constant doubling time, our td will vary with the survival rate of cells (s). For example, a cell with s=1 may have a td of 120 minutes, while a cell with s=0.5 takes twice as long to double, giving it a td of 240 minutes (120/0.5).
To calculate the number of live cells at time t, given a survival rate (s) and time (t)
- td = 120/s
- generation = t/td
- cells(t) = 2generation
To calculate the number of dead cells at time t, given a survival rate (s) and time (t)
- td = 120/s
- generation = t/td
- multiplier = (1-survival)/survival
The multiplier calculates the number of dead cells produced per cycle by each live cell.
- dead cells(t) = multiplier*(2generation-1)
To calculate the ratio of live cells/total cells, given a survival rate (s) and time (t)
- cells(t)/(cells(t)+dead cells(t))
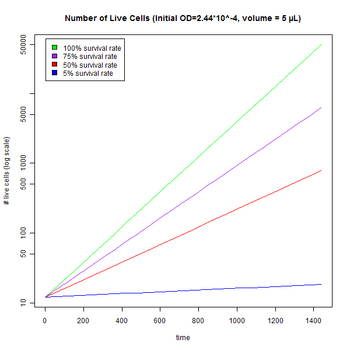
We can extend this model to calculate the number of live cells expected per culture, given an initial OD, volume, survival rate, and time.
The expected OD (if both live and dead cells contribute to OD) can be calculated from the expected numbers of live and dead cells at time t (with survival rate s).
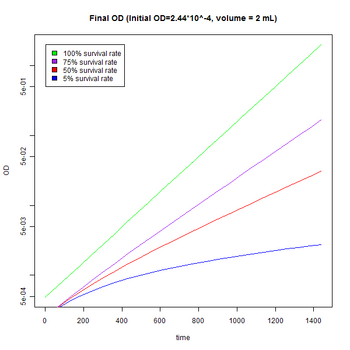
The final model of cell growth inhibition, including initial OD, volume, survival rate, and time is:
- td = 120/s
- generation = t/td
- cells(t) = OD*107*volume(mL)*2generation
- multiplier = (1-survival)/survival
- dead cells(t) = OD*107*volume(mL)*multiplier*(2generation-1)
Conclusions
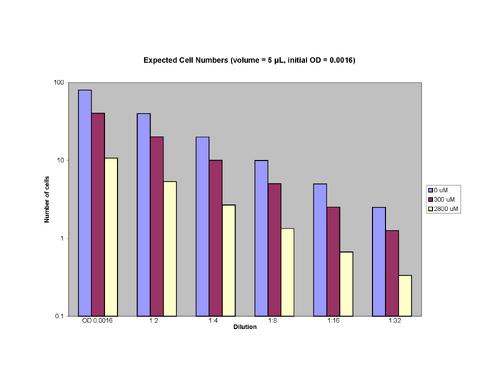
The difference between the ratios of a different survival rates is shown to be a factor of 2. So, two-fold serial dilutions of our yeast cultures would yield the most dramatic results in a YPD plate assay. Future experiments should include low initial ODs and several 2-fold dilutions.
Hypotheses
If paromomycin inhibits growth by the "survival rate" model (cells produce offspring at the same rate, but some offspring are not viable), we expect to see the following results from a plate assay:
If paromomycin inhibits growth by the "doubling time" model (cells take longer to produce offspring, but all offspring are viable), we expect to see equal cell numbers across variable drug concentrations in a plate assay (all drug concentrations would follow the blue "0 μM" model).
Results
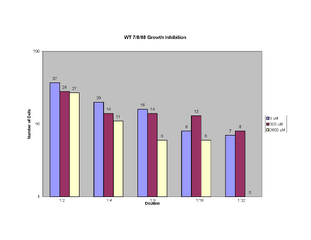
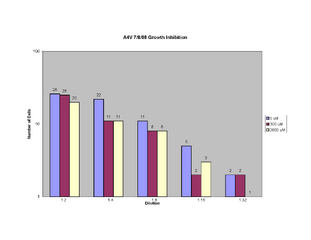
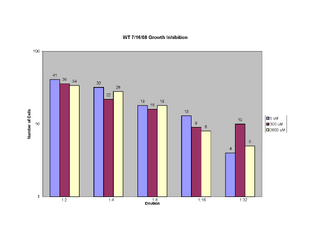
- Cell growth with varying levels of paromomycin (7/8/2008)
-
WT hSOD1 (7/8/2008)
-
A4V hSOD1 (7/8/2008)
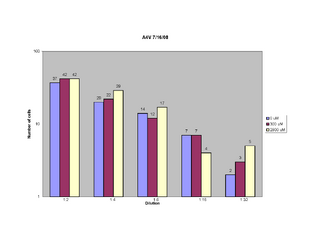
- Cell growth with varying levels of paromomycin (7/16/2008)
-
WT hSOD1 (7/16/2008)
-
A4V hSOD1 (7/16/2008)