IGEM:IMPERIAL/2006/project/Oscillator/project browser/Test Killing Predator Construct/Modelling
| Super Parts | Predator Construct | |||
|---|---|---|---|---|
| Actual Part | AiiA Testing Construct <bbpart>J37022</bbpart>
| |||
| Sub Parts | <bbpart>R0010</bbpart> | <bbpart>B0034</bbpart> | <bbpart>J37023</bbpart> | <bbpart>B0015</bbpart> |
Stage 1: Decoupling IPTG induction with AiiA Concentration
A simple model can be created for part J37022. We have assumed that the transcription of AiiA is activated by IPTG, so quasi-michaelis-menten kinetics can be applied for this model with ITPG acting as an activator. The only input we have is the concentration of IPTG. At higher values of IPTG, we expect more production of AiiA.
Assumptions:
- IPTG degradation is much longer in magnitude than AiiA degradation, so we can neglect it. IPTG is not cleaved by B-galactosidase due to the C-S bond. AiiA is LVA tagged, promoting it's degradation.
- IPTG activates transcription of the gene in michaelis-menten type kinetics with IPTG being the substrate (in high supply)
Input:
- IPTG
Output:
- AiiA concentration
Parameters:
- Vmax and Km values for IPTG activated transcription (both unknown)
We can model IPTG as an activator and use Michaelis-Menten analogues to determine a differential equation relating IPTG concentration to AiiA concentration:
At steady state, we can assume that there is no longer any change in AiiA concentration. For our experiment, we will wait a few hours before extracting the AiiA:
Thus, we can relate [AiiA] to [IPTG] in the following equation whose plot would be as shown below:
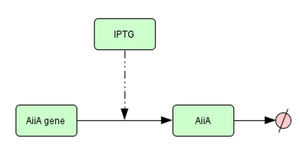
Below you can see an image of the model that we used in CellDesigner to model the part. Following our assumptions and input/output, we have modelled IPTG activated transcription of AiiA from gene and subsequent degradation.
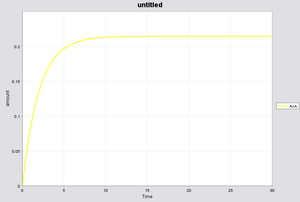
Below you can see the output simulation. As expected, with zero concentration of IPTG, no expression of AiiA occurs.
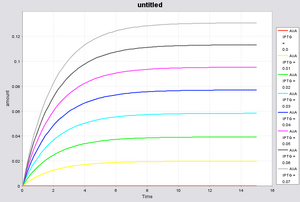
Depending upon the concentration of IPTG, the final steady state concentration of AiiA will change, as seen in the figure below.
One crucial assumption that this makes is the steady state assumption, which will no longer hold for our oscillations. Using initial conditions assuming that [AiiA] = 0 at t = 0, we can come up with an equation which will relate AiiA concentration over time by solving the differential equation above. Of course when t approaches infinity, we again obtain the expression above.
Extracting Parameters from Data
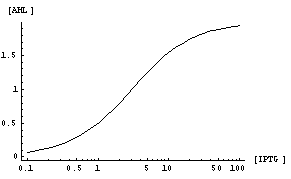
Using the immunotag, we can calculate a concentration of AiiA in solution after steady state has been reached. We will obtain a graph of [AiiA] vs. [IPTG] which we can use Matlab or Mathematica to fit our equation to extract Vmax and Km values. With these values, we can then create a calibration curve to feed into our stage 2. So, with a given amount of initial IPTG concentration, we will have a relation to a given amount of [AHL] degradation.
Calculation of the Halflife from the raw data
Assuming we already have AiiA within the cell and no IPTG inducing the production of more AiiA, then we can model the degradation of AiiA as normal first order kinetics, similar to radioactive decay. As a differential equation, we can easily write down:
The equation above can be solved and written in a linear form so that we can analyse a straight line graph as such:
\ln [AiiA] \ = c - k_{deg}t
</amsmath>Thus, if we plot ln[AiiA] vs. time, then the slope of the graph will yield the decay constant, kdeg. From this, it is easy to obtain the halflife of AiiA.
Part 2 of the halflife protocol deals with this kind of kinetics and we can easily obtain the value of the halflife by solving for kdeg, the decay constant. Intuitively, this is the easiest way of obtaining the halflife value of AiiA. However, if one analyses the production of AiiA, it might also be possible (thanks to Jimmy's observation) to calculate the halflife of AiiA simultaneously with the production of AiiA within the cell (part 1 of the halflife protocol). This will save a lot of time in testing, but ideally, we will test both to ensure we get similar results for the half-life.
So, if we consider the production of AiiA by transcription/translation within the cell as well as degradation of AiiA by cellular processes, we can express the rate of change of AiiA as a differential equation as shown below.
\frac{d[AiiA]}{dt} = k_1[mRNA]-k_{deg}[AiiA]
</amsmath>We can make some initial assumptions which will simplify our analysis. These are:
y = \frac{d[AiiA]}{dt} </amsmath> <amsmath> x = [AiiA] </amsmath> <amsmath> h=k_1[mRNA] </amsmath>
Since the concentration of mRNA is kept at a constant (we are assuming this will happen at steady state), we can rationalise the equations above to form a nice linear equation which can easily be obtained as per the equation below:
y = h - k_{deg}x
</amsmath>The slope will yield the decay constant from which the half-life can be obtained. The y-intercept will give the h value, and we can check to see if our assumption that <amsmath>h=k_1[mRNA]</amsmath> is true by making several trials of the experiment.
Calculation of the AiiA activity
As AiiA is an enzyme, we are able to use the Michaelis-Menten equation to define the activity.
We can then rearrange the Michaelis-Menten equation into the standard Lineweaver-Burk equation as shown below:
Thus, if we are able to plot a graph of 1/v vs. 1/[S], then we can linearlise the Michaelis-Menten equation and easily calculate the value for the Km and Vmax. From our raw data, we will get several plots of AHL concentration over time with varying amounts of initial AHL concentrations. We can find the initial rates of reaction by obtaining the slope of the graph at t = 0 sec. We know the starting AHL concentration which is our substrate. By plotting several of these values (i.e. several AHL concentrations), we will be able to spread out the plot and have a more accurate linear line whose slope and y-intercept will yield the activity.
In deriving the Michaelis-Menten equation, we can also derive that:
This means that the value of Vmax will vary for every concentration of AiiA we use. The Michaelis-Menten derivation assumes that the concentration of enzyme is fixed, but in our oscillating system, the concentration of AiiA will be varying continuously. So, if we can decouple the AiiA concentration from the Michaelis-Menten equation, we can easily find the value of k2, the rate constant for the converstion of the enzyme-substrate complex to separate enzyme and product. This can easily be done by inducing the system with varying amounts of IPTG and seeing the final steady state concentration of AiiA within the system. (Done as one of the experiments) Once we have decoupled IPTG concentration to Aiia concentration, we can induce the test construct at varying levels of IPTG and repeat the entire experiment to obtain another value of Vmax (Km values should be the same...so this is also a reality check). We can then use the equation above to find the value of k2, which should be constant for any system regardless of enzyme concentration or substrate concentration.