User:Yeem/20.309/Mod 2 lab report

- The Matlab scripts and raw data for this report are available here.
The AFM module required the use of an atomic force microscope to image waffles, determine Young's modulus of samples, and measure Boltzmann's constant, [math]\displaystyle{ k_B }[/math]. We tested interdigitated finger cantilevers of two lengths, 275 and 350 um.
Force calibration curves
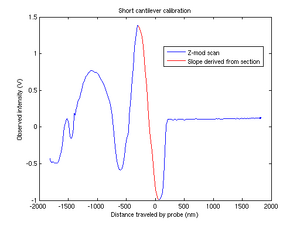
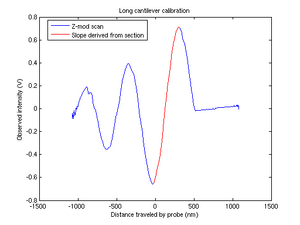
Carefully bringing the stage into contact with the cantilever, we obtained force calibration curves from the scannerGUI Z-mod scan.We began our calibrations by adjusting the bias point such that the out-of-contact line was approximately equal to the zero point of the [math]\displaystyle{ sin^2 }[/math] curve.
Our raw data was a text file of tab-separated values: a column of piezo voltages and a column of photodiode voltages. For the Boltzmann's constant section, we required dimensions of length/V. The first step was to reduce the data set to our area of interest, the first peak after initial contact. Next, we divided the photodiode voltage by our gain, [math]\displaystyle{ B }[/math] to get a normalized voltage proportional to laser intensity. The photodiode voltage was then multiplied by a correction factor, [math]\displaystyle{ A_{corr} }[/math], to account for the placement of the ID fingers relative to the length of the cantilever. Thus we have
- [math]\displaystyle{ V_{photodiode} = \{y|\forall x \in V_{photodiode}^o (y = \frac{A_{corr}}{B}x)\} }[/math]
and
- [math]\displaystyle{ A_{corr} = \frac{2}{(3m_{ID}^2-m_{ID}^3)} }[/math]
- [math]\displaystyle{ m_{ID} = \frac{L_{ID}}{L_{T}} }[/math]
where [math]\displaystyle{ L_{ID} }[/math] and [math]\displaystyle{ L_{T} }[/math] are the distance of the ID fingers from the base and the total cantilever length, respectively.
To convert the x-axis to position, we recognized that deflecting the ID fingers by [math]\displaystyle{ \frac{\lambda}{4} }[/math] (where [math]\displaystyle{ \lambda }[/math] is the wavelength of our laser, 635nm) results in moving from a relative maximum to a relative minimum. Thus our piezo to position conversion factor, [math]\displaystyle{ C_1 }[/math], was described by
- [math]\displaystyle{ C_1 = \frac{\lambda}{4 \Delta V_{piezo}} }[/math]
where [math]\displaystyle{ \Delta V_{piezo} }[/math] was the difference in piezo voltage between a peak and neighboring trough. With these conversion factors, we were able to relate our observed voltages to position vectors.
We obtained [math]\displaystyle{ C_2 }[/math], the "force" calibration, by
- [math]\displaystyle{ C_2 = |(\frac{dV_{photodiode}}{dX})^{-1}|_{V_{photodiode}=0} }[/math]
where [math]\displaystyle{ X }[/math] represented our converted position vector.
Calculating Boltzmann's constant
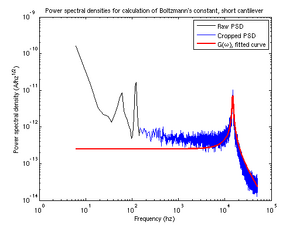
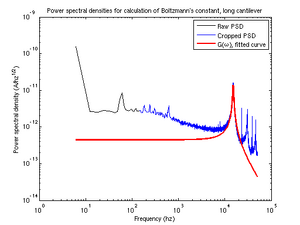
To obtain the proper dimensions for our [math]\displaystyle{ k_B }[/math] calculations, we converted our conversion factor from above (in nm/V) to angstroms/V.
- [math]\displaystyle{ C_2' = 0.1C_2 }[/math]
Then we multiplied our PSD data by the conversion factor and divided by the gain to arrive at our scaled PSD
- [math]\displaystyle{ PSD = \frac{C_2'}{B}PSD_{raw} }[/math]
in units of [math]\displaystyle{ \frac{angstroms}{\sqrt{Hz}} }[/math].
We "cropped" our data by not considering frequencies less than 100 Hz, at which "pink" noise dominates. We wisehd to generate an unscaled transfer function of the form
- [math]\displaystyle{ |G(\omega)^o| = [(1-\frac{\omega^2}{\omega_0^2})^2+\frac{\omega^2}{Q^2\omega_0^2}]^{-\frac{1}{2}} }[/math]
where [math]\displaystyle{ Q }[/math] was the quality factor and [math]\displaystyle{ \omega_0 }[/math] was the cantilever's resonant frequency. To do this, we used provided code which included transfunc.m, a scaled transfer function, and scaling.m, to do linear scaling. We used [math]\displaystyle{ lsqcurvefit }[/math] to determine the resonant frequency and quality factor of each of our cantilever lengths; these parameters were subsequently used to generate a fit.
As our initial objective was to determine Boltzmann's constant, we are reminded that our new scaled transfer function, characteristic of a second-order resonant system, can be expressed as
- [math]\displaystyle{ |G(\omega)| = \delta |G(\omega)^o| }[/math]
- [math]\displaystyle{ \delta = \sqrt{\frac{4k_BT}{Qk_s\omega_0}} }[/math]
where [math]\displaystyle{ T }[/math] is the temperature of measurement, and [math]\displaystyle{ k_s }[/math] is the Hookean spring constant of the cantilever. In the low-frequency limit,
- [math]\displaystyle{ \lim_{\omega \to 0}|G(\omega)| = \delta }[/math]
when [math]\displaystyle{ \omega }[/math]<<[math]\displaystyle{ \omega_0 }[/math]. From figure 2, the value of [math]\displaystyle{ G }[/math] is easily observable for low frequencies. The Hookean spring constant is dependent on material properties of the cantilever and is calculable by two means:
- [math]\displaystyle{ k_s = \frac{Ebh^3}{4L^3} }[/math] (from beam theory)
- [math]\displaystyle{ k_s = 0.2427\rho_chbL\omega_0^2 }[/math] (from Sader et al.)
We used the arithmetic mean of the two methods to determine Boltzmann's constant, by rearranging our equation for [math]\displaystyle{ \delta }[/math],
- [math]\displaystyle{ k_B = \frac{Qk\omega_0\delta^2}{4T} }[/math]
Using these quations, we found the following values for our cantilevers:
| Cantilever length | [math]\displaystyle{ k_s }[/math], beam theory | [math]\displaystyle{ k_s }[/math], Sader | [math]\displaystyle{ f_0 }[/math] | [math]\displaystyle{ Q }[/math] | [math]\displaystyle{ k_B }[/math] | observed/expected |
|---|---|---|---|---|---|---|
| Short (275 um) | 0.0769 | 0.0784 | 1.48e4 | 28.55 | 1.0921e-23 | 0.794 |
| Long (350 um) | 0.0373 | 0.1041 | 1.5e4 | 30.72 | 3.4476e-23 | 2.498 |
Discussion questions
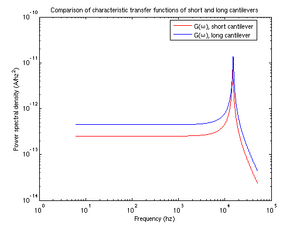
We were fairly confident that we had recorded data using two different cantilever sizes, as during our initial analysis we discovered differing resonant frequencies for our measurements. However, these differences were probably due to changes in our methods which corrected errors; we are now of the opinion that we in fact measured the Boltzmann constant using the same size cantilever twice (see figure 3).
Aside from these concerns, in determining the spring constant, we find it somewhat counterintuitive that the Sader equation relates stiffness linearly with the length of the cantilever. Longer beams must withstand higher forces due to increased mechanical advantage; deflection in the shearing plane should increase with length. We would trust the spring constant from beam theory over Sader's estimate.
We were able to measure [math]\displaystyle{ k_B }[/math] to within an order of magnitude for both sizes of cantilever. In finding our major sources of error and uncertainty, we recall our equation, which related the constant to the square of the thermomechanical noise limit.
- [math]\displaystyle{ k_B = \frac{Qk\omega_0\delta^2}{4T} }[/math]
The quality factor, spring constant, and resonant frequencies are all directly proportional to :[math]\displaystyle{ k_B }[/math], but it is [math]\displaystyle{ \delta }[/math] which dominates. Errors in delta are magnified; it is itself a function of our fit of [math]\displaystyle{ G(\omega) }[/math], which relied on our conversion factor and data collection.
We were especially concerned with the term [math]\displaystyle{ A_{corr} }[/math], which introduced an approximation which was carried throughout our calculations. To determine the distance of the ID fingers from the base, we simply averaged the beginning and end points; as the cantilever does not deflect uniformly, perhaps it would have been better to use a weighted average depending on distance from base.
Lab problem


a) Using the parameters for the longer cantilever and
- [math]\displaystyle{ \lt F_{min}\gt ^{1/2} = \sqrt{\frac{4k_BTBk_s}{Q\omega_0}} }[/math]
we arrive at 5e-13 N.
b) Femtonewton force detection is not sensitive enough to detect small biological forces.
c) The best cantilever will be a long, thin, "floppy" beam, with very low spring constant. High quality factor and resonant frequencies ensure best measurement as they result in lowest loss of energy when sampling.