User:Tyler Wynkoop/Lab ReportF
The Charge to Mass Ratio for the Electron
By Tyler Wynkoop
twynkoop@unm.edu
Abstract
Many subatomic particles have an associated electrical charge, as well as a characteristic mass. The ratio of these two numbers is an important tool for the analysis of systems containing these particles. The charge to mass ratio of the electron, in particular is of significant physical value, and is a tool for many technological and theoretical advancements, both current and historical. It can be measured by observing the competing responses of the two properties. In this lab, the radius of curvature of the electron beam, the strength of the magnetic field, and the accelerating voltage were measured. There was significant systematic error in this lab due to having to "eye" certain measurements as well as, in several instances, constants used in equations were not, in fact, constant.
Introduction
The charge and mass of the electron are both very small. They are difficult to calculate simply by direct observation. The ratio of the two, however, is relatively simple to calculate by using properties of each in combination. For mass, inertia is used. For charge, a magnetic field is used. The competition between these two effects produces a visible pattern which can be measured.
J. J. Thomson used a method very similar to this when he discovered the electron in 1897. Thomson was experimenting with cathode rays when he discovered that he could manipulate the trajectory of the ray with electric and magnetic fields. This led to the discovery of the electron, a negatively charged particle, lighter than hydrogen, with mass. This laid the ground work for further delving into the structure of the atom. (2)
In this lab, two main components were used; an electron gun and a set of Helmholtz coils. the electron gun is positioned such that the beam is perpendicular to the magnetic field generated by the coils. When the electron gun and the magnetic field are powered, the electrons in the beam curl into a circle. The electrons are accelerated by a known voltage, resulting in a known velocity. The magnetic field exerts a force perpendicular to the path of the electrons, causing the beam to arc into a circle. The stronger the magnetic field, the tighter the radius of the circle becomes.
The beam is twisted into a circle with a strong enough magnetic field, and the radius is observed. It changes with varying either the power of the field, or the velocity of the electrons, and is a function of these two. With a prescribed magnetic field and velocity, the radius is measured, and by comparing the independent variable (radius) and the dependent variables in this system, the charge to mass ratio can be calculated.
Methods and Materials
The set up to this lab was fairly simple. The electron gun, the accelerating plates, and the Helmholtz coils were combined into one apparatus, an Uchida e/m Experimental Apparatus, model tg-13. A power supply was connected to each of the components of the apparatus. The voltage of the heater supply was set at a constant 6.002 Volts and was not varied through the experiments. I used a voltmeter to guarantee the heater source voltage stayed constant throughout data collection. From the lab manual, we were asked to record two sets of data, one with constant accelerating voltage and varying magnetic field strength; and one with constant field strength and varying accelerating voltage. We took five data points for each data set, then repeated the process for a total of 10 data points for each set. I tried to vary the current powering the helmholtz coils by .2A per measurement while the voltage was held as constant as the equipment allowed, varying about .2V throughout the experiment. For the other data set, the voltage was varied by 20V while the current was held constant, the current did not vary within the sensitivity of the multimeter. I recorded the radius by "eyeing" it across the ruler set as a backdrop behind the bulb. I measured it by using the diameter. The ruler was zeroed a the center, allowing me to align my view such that the radius was the same on both sides of the zero.
The current through the Helmholtz coils dictates the strength of the magnetic field via the equation:
[math]\displaystyle{ (1) B = \frac{\mu_0 N I R^2}{(R^2+x^2)^{3/2}} }[/math]
where [math]\displaystyle{ N }[/math] is the number of loops in the coils, [math]\displaystyle{ I }[/math] is the current passing through the coils in amps, [math]\displaystyle{ R }[/math] is the radius of the coils, [math]\displaystyle{ \mu_0 }[/math] is the permeability of free space, and [math]\displaystyle{ x }[/math] is the axis of symmetry. The current through the Helmholtz coils is measured by a multimeter in series with the coils, and is prescribed by the high voltage source. This equation can be vastly simplified by using the specific equipment in my setup, where [math]\displaystyle{ x = \frac{R}{2} }[/math], [math]\displaystyle{ N = 130 }[/math], [math]\displaystyle{ R = .15 }[/math], and [math]\displaystyle{ \mu_0 }[/math] is the universal constant. Substituting in these values, the equation becomes:
[math]\displaystyle{ (2) B = (7.8 \times 10^{-4}) \times I }[/math]
Secondly, the voltage of the accelerating plates can be directly measured with the voltmeter, and is prescribed by the power source. In the tube, the radius of the electron beam is observed. On the apparatus, a measuring panel behind the tube allows for the measurement of the diameter of the circle in centimeters. However, the diameter measurements contain significant systemic error, because they must be 'eyed' against the backdrop of the measuring panel. Armed with the radius of the electron beam, the ratio can be found by:
[math]\displaystyle{ (3) \frac{e}{m} = \frac{2 \times V}{B^{2} \times R^{2}} }[/math]
Where V is the voltage across the accelerating plates, B is the strength of the magnetic field, and R is the radius of the electron beam. Here, V, B, and R are either measured or prescribed allowing for the direct calculation of e/m.
SJK 01:20, 19 December 2010 (EST)

Linking to the matlab code would be very helpful.
Results and Discussion
To analyze the data taken, I used matlab to plot the best fit lines as well as to find the standard deviation.
Firstly is the data taken under constant voltage:
Trial 1 yielded an e/m of [math]\displaystyle{ 1.27(7) \times 10^{11} \frac{C}{Kg} }[/math]
Trial 2 yielded an e/m of [math]\displaystyle{ 1.3(7) \times 10^{11} \frac{C}{Kg} }[/math]
Combining these results yields an e/m of [math]\displaystyle{ 1.31(8) \times 10^{11} \frac{C}{Kg} }[/math] The accepted value for e/m is [math]\displaystyle{ 1.76 \times 10^{11} \frac{C}{Kg} }[/math], this yields an error of 26±4%.SJK 01:22, 19 December 2010 (EST)

The methods seem to be missing description of how (or why) you combine these measurements. There seems to be an error, though, since your combined result is outside of the two values, and also has a larger uncertainty.
Secondly, the data taken under constant current:
Trial 1 yielded an e/m of [math]\displaystyle{ 1.5(2) \times 10^{11} \frac{C}{Kg} }[/math]
Trial 2 yielded an e/m of [math]\displaystyle{ 1.6(2) \times 10^{11} \frac{C}{Kg} }[/math]
Combining these results yields an e/m of [math]\displaystyle{ 1.5(2) \times 10^{11} \frac{C}{Kg} }[/math] Comparing with the accepted value yields an error of 12±12%.
SJK 01:25, 19 December 2010 (EST)

Figures need a description in addition to the title
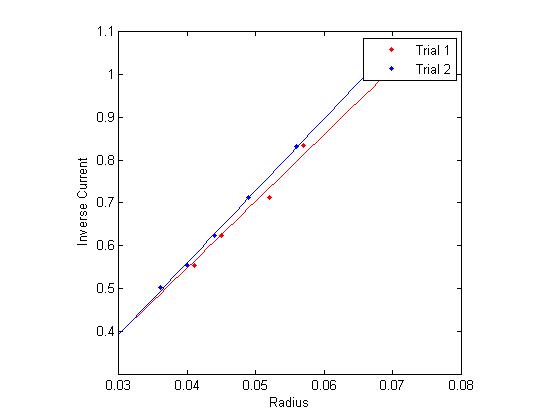 Figure 1: Inverse current vs. Radius
Figure 1: Inverse current vs. Radius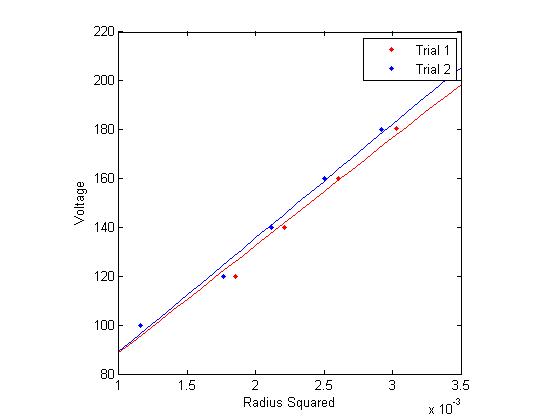 Figure 2: Voltage vs. Radius Squared
Figure 2: Voltage vs. Radius Squared
The final method of calculating the e/m is by analyzing the slope of several functions derived directly from the data, namely, inverse current as a function of radius and voltage as a function of radius squared. This comes directly from equations (1) and (3).
Using linear regression on this data (in the graphs to the right), and multiplying by appropriate constants yields several more estimates for e/m.
For the data shown in figure 1: [math]\displaystyle{ 1.115 \times 10^{11} \frac{C}{Kg} }[/math]
For the data shown in figure 2: [math]\displaystyle{ 1.180 \times 10^{11} \frac{C}{Kg} }[/math]
In both cases above, the result for e/m has a much higher error than previous estimates. This is most likely due, once again, to the large systematic error in the lab.
The most striking thing about this data is difference in the results for constant current and constant voltage. With constant voltage, the absolute error was significantly higher, but the consistency was also higher. The constant voltage yielded low accuracy but high consistency, conversely, the constant current measurements yielded a much more accurate answer, but with much lower consistency. This was most likely due to the degree of control on the voltage. It was very difficult to get a constant voltage according to the voltmeter. Even in the tests where the voltage was to remain "constant," it varied several tenths of a volt. This could easily have caused the inconsistency in the constant voltage tests. The current, however, was easy to control to a high degree. This would yield an accurate average, but a high standard deviation, which is what was observed.
Conclusions
In order to measure the e/m ratio, and experimentalist needs accurate equipment. The greatest difficulty in this lab was the difficulty in controlling the accelerating voltage. Secondly, the multimeters provided were only capable of sensitivity out to a single decimal when the order of magnitude was hundreds of volts. With more accurate multimeters and a more stable high voltage source, the measurement of the e/m ratio could become quite accurate. Finally, the diameter measurements had to be "eyed" against the measuring panel on the backdrop. With digital equipment, or perhaps a measuring device inside the electron tube, the radius measurements could be increased in accuracy by a significant digit or perhaps even two. The combination of these would make measuring the e/m ratio for the electron extremely accurate.
Another large source of systematic error came from the heater voltage. The heater voltage is merely to generate the electrons, but when I modified the this voltage, the radius changed. It was a relatively small amount, but considering it should only change the intensity of the beam, this could have been a substantial source of error.SJK 01:30, 19 December 2010 (EST)

This is a very good point.
Acknowledgements
I thank Dan Wilkinson for recording the data.
Steve Koch and Katie Richardson for their expertise and guidance in the lab.
References
SJK 01:31, 19 December 2010 (EST)

More peer-reviewed sources needed.
Michael Gold, University of New Mexico Physics 307L Laboratory Manual.
Thomson, George Paget. (1964) J.J. Thomson: Discoverer of the Electron. Great Britain: Thomas Nelson & Sons, Ltd (1)
J.J. Thomson (1897), Cathode rays, Philosophical Magazine, 44, 293 — Discovery of the electron (2)