User:Tyler Wynkoop/Lab Report
Steve Koch 01:34, 19 December 2010 (EST):Lots of good improvements over rough draft, but still some things missing.
The Charge to Mass Ratio for the Electron
SJK 05:26, 8 December 2010 (EST)

This is decent title and author/contact.
By Tyler Wynkoop
twynkoop@unm.edu
Abstract
SJK 05:22, 8 December 2010 (EST)

This is a good start. You should finish it by saying something like, "In this report we measure the ratio by measuring the radius of curvature of an electron beam blah blah. We found significant systematic error and discuss the sources.
Many subatomic particles have an associated electrical charge, as well as a characteristic mass. The ratio of these two numbers is an important tool for the analysis of systems containing these particles. The charge to mass ratio of the electron, in particular is of significant physical value, and is a tool for many technological and theoretical advancements, both current and historical. It can be measured by observing the competing responses of the two properties.
Introduction
SJK 05:32, 8 December 2010 (EST)

As it stands now, your introduction reads well but is mostly about your method for measuring the charge to mass ratio. That may be OK, provided you expand it to include the other necessary parts, and also provided you detail the methods in the methods section (I haven't looked at that yet). For this introduction, the main and most difficult thing you need is a background on how this quantity has been measured in the past. This will also allow you to put in some citations to original peer-reviewed research reports, which you will need to find.
The charge and mass of the electron are both very small. They are difficult to calculate simply by direct observation. The ratio of the two, however, is relatively simple to calculate by using properties of each in combination. For mass, inertia is used. For charge, a magnetic field is used. The competition between these two effects produces a visible pattern which can be measured.
In this lab, two main components were used; an electron gun and a set of Helmholtz coils. the electron gun is positioned such that the beam is perpendicular to the magnetic field generated by the coils. When the electron gun and the magnetic field are powered, the electrons in the beam curl into a circle. The electrons are accelerated by a known voltage, resulting in a known velocity. The magnetic field exerts a force perpendicular to the path of the electrons, causing the beam to arc. If the magnetic field is strong enough, the beam will arc into a circle.SJK 05:29, 8 December 2010 (EST)

technical it's always a circle if the beam isn't losing energy, right? It just hits the bulb.
However, the momentum opposes this arcing pattern, causing the beam to straighten.
The beam is twisted into a circle with a strong enough magnetic field, and the radius is observed. It changes with varying either the power of the field, or the velocity of the electrons, and is a function of these two. With a prescribed magnetic field and velocity, the radius is measured, and by comparing the independent variable (radius) and the dependent variables in this system, the charge to mass ratio can be calculated.
Methods and Materials
SJK 05:37, 8 December 2010 (EST)

What you have written here is good--main issue is that it is a mix of past and present tense, mostly present. It should be mostly past tense--"we did," since your goal is to describe exactly what you did, not what you wanted to do. Also, there are some things missing about your methods, that would inhibit reproducibility. How did you set out to obtain your data? Were there important things, such as filament voltage? How long you let it warm up? Did you use the right or left side of the beam? What software did you use to analyze the data? What were the analysis methods? All of these things should be in the methods to ensure reproducibility.
The set up to this lab is fairly simple. The electron gun, the accelerating plates, and the Helmholtz coils are combined into one apparatus, an Uchida e/m Experimental Apparatus, model tg-13. A power supply is connected to each of the components of the apparatus. The voltage of the heater supply was set at a constant 6.002 Volts and is not varied through the experiments. I used a voltmeter to guarantee the heater source voltage stayed constant throughout data collection.
The current through the Helmholtz coils dictates the strength of the magnetic field via the equation:
[math]\displaystyle{ (1) B = \frac{\mu_0 N I R^2}{(R^2+x^2)^{3/2}} }[/math]
where [math]\displaystyle{ N }[/math] is the number of loops in the coils, [math]\displaystyle{ I }[/math] is the current passing through the coils in amps, [math]\displaystyle{ R }[/math] is the radius of the coils, [math]\displaystyle{ \mu_0 }[/math] is the permeability of free space, and [math]\displaystyle{ x }[/math] is the axis of symmetry. The current through the Helmholtz coils is measured by a multimeter in series with the coils, and is prescribed by the high voltage source. This equation can be vastly simplified by using the specific equipment in my setup, where [math]\displaystyle{ x = \frac{R}{2} }[/math], [math]\displaystyle{ N = 130 }[/math], [math]\displaystyle{ R = .15 }[/math], and [math]\displaystyle{ \mu_0 }[/math] is the universal constant. Substituting in these values, the equation becomes:
[math]\displaystyle{ (2) B = (7.8 \times 10^{-4}) \times I }[/math]
Secondly, the voltage of the accelerating plates can be directly measured with the voltmeter, and is prescribed by the power source. In the tube, the radius of the electron beam is observed. On the apparatus, a measuring panel behind the tube allows for the measurement of the diameter of the circle in centimeters. However, the diameter measurements contain significant systemic error, because they must be 'eyed' against the backdrop of the measuring panel. Armed with the radius of the electron beam, the ratio can be found by:
[math]\displaystyle{ (3) \frac{e}{m} = \frac{2 \times V}{B^{2} \times R^{2}} }[/math]
Where V is the voltage across the accelerating plates, B is the strength of the magnetic field, and R is the radius of the electron beam. Here, V, B, and R are either measured or prescribed allowing for the direct calculation of e/m.
Results and Discussion
SJK 05:51, 8 December 2010 (EST)

This section presents some good results. However, there isn't enough description/discussion. As of now, it's close to just a bulleted list of results. Also, the section "matlab code issue" makes me think you weren't quite finished with this anyway.
We took four sets of data, two with constant magnetic field strength, two with constant accelerating voltage, with five data points each.
Firstly is the data taken under constant voltage:
SJK 05:44, 8 December 2010 (EST)

Too many digits of precision on the values. Since error is 0.07E11, it would be much easier to read as (1.27 +/- 7) *10^11 or 1.27(7) *10^11. The uncertainty is almost always one digit, maybe two if the first digit is small
Trial 1 yielded an e/m of [math]\displaystyle{ 1.2746 \times 10^{11} \pm 7.00 \times 10^{9} \frac{C}{Kg} }[/math]
Trial 2 yielded an e/m of [math]\displaystyle{ 1.3383 \times 10^{11} \pm 7.29 \times 10^{9} \frac{C}{Kg} }[/math]
Combining these results yields an e/m of [math]\displaystyle{ 1.3065 \times 10^{11} \pm 7.82 \times 10^{9} \frac{C}{Kg} }[/math] The accepted value for e/m is [math]\displaystyle{ 1.76 \times 10^{11} \frac{C}{Kg} }[/math], this yields an error of 26±4%.
Secondly, the data taken under constant current:
Trial 1 yielded an e/m of [math]\displaystyle{ 1.5334 \times 10^{11} \pm 2.24 \times 10^{10} }[/math]
Trial 2 yielded an e/m of [math]\displaystyle{ 1.5786 \times 10^{11} \pm 2.02 \times 10^{10} }[/math]
Combining these results yields an e/m of [math]\displaystyle{ 1.5560 \times 10^{11} \pm 2.14 \times 10^{10} \frac{C}{Kg} }[/math] Comparing with the accepted value yields an error of 12±12%.
SJK 05:50, 8 December 2010 (EST)

These figures will need to be numbered, have a title, and more of a description, so that the reader could understand them somewhat. They will also need to be referred to in the text and the results discussed in the text.
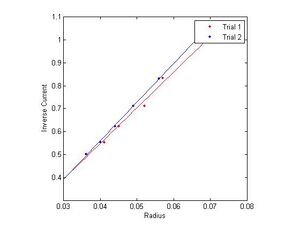
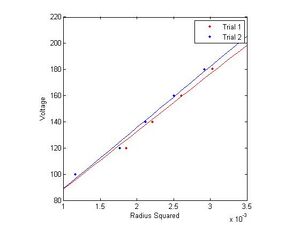
The final method of calculating the e/m is by analyzing the slope of several functions derived directly from the data, namely, inverse current as a function of radius and voltage as a function of radius squared. This comes directly from equations (1) and (3).
Using linear regression on this data (in the graphs to the right), and multiplying by appropriate constants yields several more estimates for e/m. SJK 05:46, 8 December 2010 (EST)

I gather you will report these values in the final report? Also, above, you should compare how many standard deviations away from the accepted value you are (a lot). Given all the values you're calculating, seems that a table would be in order.
Matlab Code Issue
The most striking thing about this data is difference in the results for constant current and constant voltage. With constant voltage, the absolute error was significantly higher, but the consistency was also higher. The constant voltage yielded low accuracy but high consistency, conversely, the constant current measurements yielded a much more accurate answer, but with much lower consistency. This was most likely due to the degree of control on the voltage. It was very difficult to get a constant voltage according to the voltmeter. Even in the tests where the voltage was to remain "constant," it varied several tenths of a volt. This could easily have caused the inconsistency in the constant voltage tests. The current, however, was easy to control to a high degree. This would yield an accurate average, but a high standard deviation, which is what was observed.
Conclusions
SJK 06:08, 8 December 2010 (EST)

I like this section, but disagree with your conclusions. Why would more precise instrumentation improve the accuracy? To do that, you need to get rid of systematic error. What is the dominant source of the systematic error? You should explore that in your follow-on data.
In order to measure the e/m ratio, and experimentalist needs accurate equipment. The greatest difficulty in this lab was the difficulty in controlling the accelerating voltage. Secondly, the multimeters provided were only capable of sensitivity out to a single decimal when the order of magnitude was hundreds of volts. With more accurate multimeters and a more stable high voltage source, the measurement of the e/m ratio could become quite accurate. Finally, the diameter measurements had to be "eyed" against the measuring panel on the backdrop. With digital equipment, or perhaps a measuring device inside the electron tube, the radius measurements could be increased in accuracy by a significant digit or perhaps even two. The combination of these would make measuring the e/m ratio for the electron extremely accurate.
Acknowledgements
SJK 05:53, 8 December 2010 (EST)

For the formal report, the acknowledgements need to be in paragraph / sentence format. E.g., "I thank Dan Wilkinson for assistance in data acquisition." etc.
Dan Wilkinson, my lab partner
Steve Koch, my lab professor
Katie Richardson, my lab TA
References
SJK 05:54, 8 December 2010 (EST)

You will need several references that are peer-reviewed original research papers. Likely, you will find it easiest to work these into the introduction, where you will talk about background to your measurements.
Michael Gold, University of New Mexico Physics 307L Laboratory Manual.
Thomson, George Paget. (1964) J.J. Thomson: Discoverer of the Electron. Great Britain: Thomas Nelson & Sons, Ltd
Overall SJK Comments
05:57, 8 December 2010 (EST): This is a well-written rough draft. There are some missing things as described above. For the follow-on data today, I'm going to recommend similar to Alex, which are on the following link. It has to do with finding the sources of the systematic error: http://openwetware.org/wiki/Physics307L:People/Benedict/Draft