User:Michael R Phillips/Notebook/Physics 307L/Entry Base
 Oscilloscope Lab Oscilloscope Lab
|
|
|
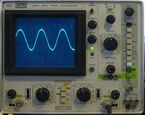
Set Up I started by hooking up the Function Generator to the Oscilloscope from "Output" to "CH 1" and turning both instruments on. After setting the generator to a sine wave and to a frequency that displays nicely on the oscilloscope, the wave was still not steady; it was moving very quickly across the screen. After messing with the dials a bit, I found that moving the trigger caused the wave to stabilize. After some more careful adjustments, I obtained a centered sine wave with a good amplitude and frequency for measurement. Measurement
From looking at the grid lines after adjusting the "Volts/Div" knob so that the wave peaks and troughs just touch the top of the viewing part of the oscilloscope, I could estimate the amplitude as 500mV. The period is about 160ms. Since each grid line measures 25.0ms and the period is observed as just barely under 6.5 grid lines, 160ms seems a reasonable measurement.
Now setting the wave so that the peaks and troughs were at half the max height of the oscilloscope (without changing the output level of the generator), I measured the distance between a trough and a peak to be 4.08V, suggesting an amplitude of 2.04V. Correction to using grid lines: my previous estimate of 500mV was off because I assumed the displayed grid measurements corresponded to the maximums and minimums of the viewing window when they in fact correspond to the individual grid lines. My old estimate would now be 2V. The period, using the same method, is determined to be 161.0ms. This is also displayed as a frequency, 6.21Hz.
The peak to trough measurement (Pk-Pk) switches from 4.04V to 4.08V and back , apparently from the accuracy of the measure function. This implies an amplitude of 2.02V to 2.04V. The period using the measure function varies between 160.3ms and 161.1ms. This appears to be due to the accuracy that the oscilloscope is trying to obtain.
For higher amplitudes measuring to the same degree of accuracy as above (i.e. Pk-Pk of between 9 and 10 Volts), the measure function seems to work better, but the inaccuracy remains at the lower amplitudes (i.e. Pk-Pk lower than 2 Volts). At very large DC Offsets, the waveform completely breaks down and the oscilloscope displays a question mark when trying to measure the period, suggesting it is unsure of the values it is displaying. The same kind of thing happens also at very low DC Offsets. The oscilloscope seems to have no problem with high frequency, but it does have a problem with very low frequency (high period). Triggering The reason we would want to trigger on a rising edge is so that we see our sine wave (or whatever) starting at zero and rising to its maximum value. We could certainly do falling edge if we want; this shifts the phase by 90 degrees but has the same measurements in the end. In changing the coupling from DC to everything else, we can see some change. Noise reject shifts the wave a little to the left, perhaps accounting for background interference. HF reject gives a smooth return, while LF reject gives a moving (horizontally) return. AC coupling just seems to shift the waveform a little to the right (30 degree phase shift maybe?). AC Coupling It took some time to achieve the shape needed for the AC coupling part, but I managed to get it displayed soon enough. After following the directions from the lab page (square wave, zero DC offset, amplitude about 8.6V), I switched things around a little bit, ending up with a maximum on the AC coupling figure of about 16.0V. To find the fall time, I set a Voltage cursor to the peak (16.0V) and one at the 10% point (1.60V) to the best accuracy I could. Next, I placed Time cursors to intersect the figure at the same place that the Voltage cursors just did, and I obtained a fall time of 52.0ms. Using measure to get a fall time, I obtained about 54ms (because the measurement varies slightly. The RC constant corresponds to the fall time exactly, so this is between 52 and 54 ms. (This relation taken from work by Zane As for checking the accuracy of this fall time, we know that t=R*C, so if we could find the resistance and capacitance of the system, we could easily find the true fall time.
| |