User:Kirstin Grace Harriger/Notebook/Physics 307L/Electron Charge to Mass Ratio
Steve Koch 03:56, 21 December 2010 (EST):Very good lab notebook. I think, though, and error in one of your analysis methods that you should have pursued. Big systematic error is unavoidable in this lab, but not 2 orders of magnitude.}}
Lab 05: Electron Charge to Mass Ratio
Concepts
- E/M Ratio: The quantity representing the ratio of an electron's charge to it's mass was experimentally sought after for the first time by J. J. Thomson in 1897 using cathode ray tubes. He is also credited with the discovery of the electron itself. Using a gas sample between two charged plates Thomson was able to observe a current as the electrons interacted with the gas atoms and caused them to ionize. By applying a magnetic field, he could alter the path of the current and observe the change. Using Maxwell's theories and some geometry he was able to calculate the charge to mass ratio of an electron based on measurements of the current's path.
Safety Concerns
- Be aware of shock hazards
Equipment
- SOAR DC Power Supply Model PS-3630 - used to power the heater
- e/m Experimental Apparatus -composed of a tube of dilute helium gas, an electron heater, focusing magnets, and a Helmholtz coil used to provide a constant magnetic field
- Gelman Instrument Company: Deluxe Regulated Power Supply
- Hewlett Packard 6384A DC Power Supply
Set-Up
Connections
- SOAR output minus to lower plug on heater
- SOAR output plus to upper plug on heater side
- Gelman plugs on back into electrode plug on e/m device
- Red to positive
- Black to negative
- Volt meter plugs onto multimeter
- Helmholtz on e/m to HP power supply
Multimeters
- ammeter -connected in series with the Helmholtz coil to measure the current going into the coils,
- voltmeter -connected in parallel with to ensure the voltage on the heater does not exceed 6.3 V,
- voltmeter -connected in parallel to the electrode to measure the voltage at which the electrons are fired at.
The final set up.
Procedure
We turned on the heater for the electron gun and let it warm up for a few minutes. Then we raised its initial voltage to 6.3 V as measured from the voltmeter. This voltage was kept constant for the duration of the experiment. Then we raised the acceleration voltage of the electrons and focused the beam into a line firing to the right.
After tuning the electron beam, we measured the current passing through the Helmholtz coils and the voltage of the electrons. By adjusting the current going into the Helmholtz coil, we were able to change the path of the electrons by bending it. A higher current resulted in a higher magnetic field acting on the electrons. This caused a tighter coil to form. Adjusting the accelerating potential on the electrons also changed their pattern. A higher voltage resulted in a wider circle.
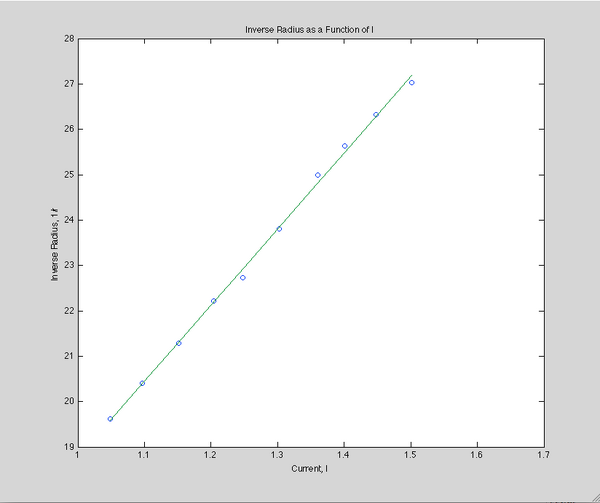
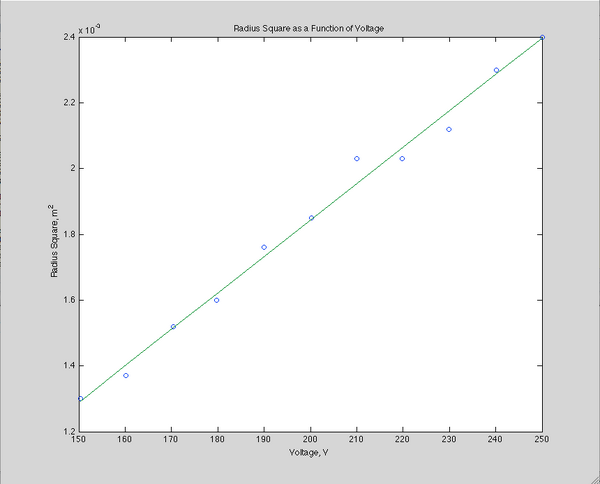
We then made twenty measurements. For the first ten, we kept the accelerating voltage constant near 200 V, and adjusted the current of the Helmholtz Coil from approximately 1.05 A to 1.5 A in steps of 0.05 A. The last ten measurements were conducted by maintaining a constant current, at 1.125 A, and adjusting the voltage from 150 V to 250 V in steps of 10 V.
To measure the radius of the beam, we aligned the beam with its reflection on the ruler behind the bulb, and recorded the marking that they crossed. We measured the radius on both the left and right sides, but we decided to only use only the radius on the right for analysis. We reasoned this was the better choice because the one on the left is more likely to change depending on the interactions that it goes through with the helium in the tube. (Steve Koch 03:55, 21 December 2010 (EST):I agree with this reasoning)
Data
{{#widget:Google Spreadsheet |key=0AjJAt7upwcA4dFpiSk1kcXc2SFZTS3hSQkNXekVYa0E |width=625 |height=400 }}
Analysis
To determine the magnetic field, we used the following formula:
[math]\displaystyle{ B = \frac {\mu R^2 N I}{(R^2+x^2)^{3/2}} }[/math]
where: B - the magnetic field, in Telsa, μ - permeability of free space, 4π * 10-7 weber/ amp-meter2, R - radius of the rings, 0.15 m, N - number of times the wires go around the Helmholtz coil, 130 times, I - current measured in A, x - the axis where the measurement is taken, in this case x=R/2
[math]\displaystyle{ B = (7.8*10^{-4} \frac {weber}{amp-meter^2} )* I }[/math]
In order to find the e/m ratio from the data, we need to find the relationship of the ratio of e/m to our data. Using the follow formulas we can determine the e/m ratio:
[math]\displaystyle{ eV= \frac {mv^2}{2} }[/math]
[math]\displaystyle{ F_B = qvB \, }[/math]
where: e and q - the charges of the electron, V - the acceleration potential, v - the velocity the charges travel at, FB - the force due to the magnetic field, and B - the external magnetic field
Together, these equations give the e/m ratio:
[math]\displaystyle{ \frac {e} {m} = \frac {2V} {r^2 B^2} }[/math]
The first method to find the e/m ratio from the data is to plot the inverse of the radius versus the current at a constant accelerator voltage. This gives a simple linear relationship:
[math]\displaystyle{ \frac {1} {r} = \sqrt {\frac {(7.8*10^{-4})^2}{2V} \frac {e}{m}} I }[/math]
The second method to find the e/m ratio from the data is to graph the radius squared versus the acceleration potential at a constant current. This linear relationship is given by:
[math]\displaystyle{ r^2 = \frac {2V} {(7.8*10^{-4})^2 I} * \frac {m}{e} }[/math]
{{#widget:Google Spreadsheet |key=0AjJAt7upwcA4dGY0ZDloU3A2ZVBMUjE4UUR4QzBLTEE |width=750 |height=475 }}
Using MATLAB for linear regression and the method of least squares, we found the best fit lines for varying current and varying voltage and used their slopes to calculate the e/m ratio from the two methods described above.
The first method gives us a slope of s=16.8179.
[math]\displaystyle{ \frac {e}{m} = \frac {2s^2 V}{(7.8*10^{-4})^2} }[/math]
This produces a ratio of 1.10571*1010 C/kg.
The second method gives a slope of s=1.111*10-5.
[math]\displaystyle{ \frac {e} {m} = \frac {2} {s(7.8*10^{-4} I)} }[/math]
This then gives a ratio of e/m =1.84*108 C/kg.
The currently accepted value is:
- [math]\displaystyle{ \frac{e}{m}=1.76\times10^{11}\frac{C}{kg}\,\! }[/math]
Resources
Collaboration
- My lab partner Brian Josey
