User:Justin Roth Muehlmeyer/Notebook/307L Notebook/Planck

^{SJK Incomplete Feedback Notice}

Incomplete Feedback Notice
My feedback is incomplete on this page for two reasons. First, the value of the feedback to the students is low, given that the course is over. Second, I'm running out of time to finish grading!

Instrumentation

TEKTRONIX TDS 1002 Two Channel Digital Oscilloscope

PASCO Scientific Hg Light Source, model OS-9286

Wavetek True RMS multimeter, model 85XT

Experiment 1 Data

Part A. Green

• we placed the relative transmission filter, and the "green filter" on the white reflective mask.

100% relative transmission percentage

• Trial 1
• Voltage: 0.836 V
• Time to return to Voltage after reset: 10.19 S

• Trial 2
• Voltage: 0.837 V
• Time: 10.61 S

80% relative transmission percentage

• Trial 1
• Voltage: 0.837 V
• Time: 17.25 S

• Trial 2
• Voltage: 0.837 V
• Time: 12.85 S

60% relative transmission percentage

• Trial 1
• Voltage: 0.835 V
• Time: 13.48 S

• Trial 2
• Voltage: 0.836 V
• Time: 17.95 S

40% relative transmission percentage

• Trial 1
• Voltage: 0.836 V
• Time: 24.45 S

• Trial 2
• Voltage: 0.836 V
• Time: 21.23 S

20% relative transmission percentage

• Trial 1
• Voltage: 0.834 V
• Time: 33.74 S

• Trial 2
• Voltage: 0.835 V
• Time: 43.80 S

NOTE: We realize now we were supposed to measure all of these times to the "SAME" voltage. We misinterprested this from Gould's manual. We might have to redo this data if our analysis goves us a value that is not descent.

Part A. Yellow

100% relative transmission percentage

• Trial 1
• Voltage: 0.704 V
• Time: 7.82 S

• Trial 2
• Voltage: 0.705 V
• Time: 13.34 S

• Trial 3
• Voltage: 0.705 V
• Time: 11.31 S

80% relative transmission percentage

• Trial 1
• Voltage: 0.705 V
• Time: 10.12 S

• Trial 2
• Voltage: 0.705 V
• Time: 10.54 S

• Trial 3
• Voltage: 0.706 V
• Time: 14.95 S

60% relative transmission percentage

• Trial 1
• Voltage: 0.706 V
• Time: 23.54 S

• Trial 2
• Voltage: 0.706 V
• Time: 19.62 S

• Trial 3
• Voltage: 0.706 V
• Time: 11.80 S

40% relative transmission percentage

• Trial 1
• Voltage: 0.704 V
• Time: 33.04 S

• Trial 2
• Voltage: 0.704 V
• Time: 29.13 S

• Trial 3
• Voltage: 0.704 V
• Time: 38.07 S

20% relative transmission percentage

• Trial 1
• Voltage: 0.700 V
• Time: 39.18 S

• Trial 2
• Voltage: 0.700 V
• Time: 44.7 S

• Trial 3
• Voltage: 0.700 V
• Time: 46.38 S

Part 1 B

coming from the right...

Trial 1:

• Yellow: 0.714 V
• Green: 0.849 V
• Right Blue: 1.488 V
• Middle Blue: 1.710 V
• Left Blue: 2.053 V

Trial 2:

• Yellow: 0.711 V
• Green: 0.830 V
• Right Blue: 1.499 V
• Middle Blue: 1.710 V
• Left Blue: 2.030 V

Trial 3:

• Yellow: 0.706 V
• Green: 0.846 V
• Right Blue: 1.477 V
• Middle Blue: 1.722 V
• Left Blue: 2.067 V

Experiment 2 Data

batteries tested once more...good

Order 1

Recording stoppping Potential:

Orange

• Trial 1: 0.711 V
• Trial 2: 0.710 V

Green

• Trial 1: 0.840 V
• Trial 2: 0.841 V

Right Blue

• Trial 1: 1.479 V
• Trial 2: 1.480 V

Middle Blue

• Trial 1: 1.667 V
• Trial 2: 1.671 V

Left Blue

• Trial 1: 1.994 V
• Trial 2: 2.002 V

Order 2

we re-focused the lens to obtain nice, strong, distinct spectral lines.

Orange

• Trial 1: 0.650 V
• Trial 2: 0.655 V
• Trial 3: 0.663 V
• Trial 4: 0.684 V

Green

• Trial 1: 1.204 V
• Trial 2: 1.229 V (photons gone wild)
• Trial 3: 1.221 V
• Trial 4: 1.226 V

Right Blue

• Trial 1: 1.427 V
• Trial 2: 1.435 V
• Trial 3: 1.451 V
• Trial 4: 1.470 V

Middle Blue

• Trial 1: 1.610 V
• Trial 2: 1.628 V
• Trial 3: 1.668 V
• Trial 4: 1.675 V

Left Blue

• Trial 1: 1.992 V
• Trial 2: 1.988 V
• Trial 3: 2.023 V
• Trial 4: 2.024 V

NOTE: Notice how we took four trials in this case due to the odd fluctuations in our data. We found that our voltages kept increasing for each trial. We are not completely sure of what this means. Why do our stopping potentials keep increasing as we take more data? My only explanation is the temperature of the lamp. The lamp was exceedingly warm by this point since it had been on for several hours. Is it possible that the lamp was emitting higher frequencies due to the fact that it had been on for too long? Is it possible that over time the lamp begins to pump a bit too much electric current into the mercury gas that it begins to emit higher frequencies? If it was only mercury in the lamp, why would it begin emitting higher frequencies?

I decided to scrap the third and 4th trials in my data analysis since the voltages just continued increasing for whatever reason.

Data Analysis

See my data anlaysis worksheet

File:Planck Analysis.xls

Experiment 1

Trial 1

Vstop vs. Transmission	Charge Time vs. Transmission

Trial 2

Vstop vs. Transmission	Charge Time vs. Transmission

Question 1: Describe the effect of the varying intensity on the stopping potential.

• As one can see from my plots the stopping potential varies on the order of a a few thousands of a Volt as we vary the intensity via the transmission filter. During the experiemtn we noticed that the voltage fluctuates at this same range for no apparent reason (maybe moving my hands around, or breathing) and so we can conclude that these variations in the potential are meaningless. That of course means that the stopping potential, and therefore the kinetic energy of the photo electrons is not dependent on the intensity of light.

Question 2: Describe the effect that different colors of light had on the stopping potential.

• The shorter wavelength light produces higher stopping potentials. This validates the fact that higher energy frequencies (shorter wavelength) have more energy to give to the photoelectrons, thus the photoelectrons receive more energy from higher frequencies and are able to leave the metal with a higher kinetic energy.

Question 3: Does this support wave thoeory of light or quantum?

• The old wave theory of light predicted that the kinetic energy of the photons would depend on the intensity of the incident light. Since we have shown this is not the case we have proven the wave theory of light invalid. The quantum theory of light, based on this experiment, is the new doctrine...that the kinetic energy of photo-electrons depend on the incident frequency, not intensity. We can show that this is most certainly the case by simply looking at teh stopping potentials of each color...

Color	Max Voltage Trial 1	Max Voltage Trial 2
Yellow	0.714 V	0.711 V
Green	0.849 V	0.830 V
Blue	1.488 V	1.499 V
Violet	1.710 V	1.710 V
Ultraviolet	2.053 V	2.030 V

A trend can be seen that the higher the frequency (highest is ultraviolet at 8.20E14 Hz) of incident light, the higher the kinetic energy of the photoelectrons as indicated by the stopping potential.

Question 4: Explain why there is a slight drop in the measured stopping potential as the light intensity is decreased.

• My Yellow line plot is the best example fo this, where the stopping potential does indeed drop beginningat about 20% intensity transmission. The lab manual says this is due to the high impedence amplifier that lets us measure the stopping potential right from the anode of the plate using a voltmeter. Charge leaks off, meaning that if it takes longer for the capacitor to charge up, it will leak more...kind of like a bath tub that drains. If you fill it up at a higher rate the leaking is neglible. But if you fill it up slow, the draining makes a bid difference. At low intensity light, the capacitor takes a while to charge up and thus the current drain is noticed.

Conclusion of Experiment 1:

We have validated the photon theory of light and can now proceed to determine the exact relationship between the frequency of incident light and the Kinetic Energy of these photo-electrons being emitted...

Determination of h

Einstein's nobel prize relationship between incident frequency of light and the kinetic energy of the emitted photons is...

[math]\displaystyle{ hf=W_{o}+KE }[/math]

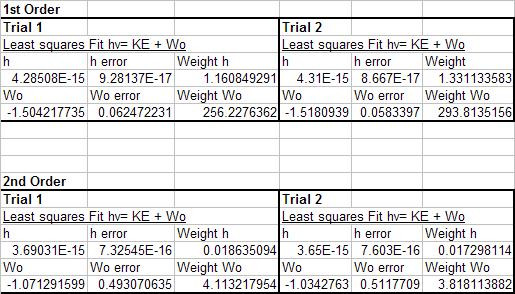
where we set out to determine the constant h by altering the equation to put it into a form that allows us to use the method of linear least squares...

[math]\displaystyle{ Vo=\frac{h}{e}f - \frac{W_{o}}{e} }[/math]

Plots with linear least squares best fit lines...

1st Order Trial 1	1st Order Trial 2

2nd Order Trial 1	2nd Order Trial 2

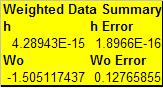
According to Taylor, when we have two measuremtns with inconsistent or unequal uncertainties then we can not take a simple average of the two numbers and expect a "best" estimate. We must take the weighted average which accounts for the fact that more precise measurements should be given more weight.

^{SJK 18:41, 18 December 2008 (EST)}

18:41, 18 December 2008 (EST)
However...I don't think the weighted average is justified, since there is clearly a disagreement between the two data sets (caused in large part by the 2nd order green band problem).

[math]\displaystyle{ \bar{x} = \frac{ \sum_{i=1}^n w_i x_i}{\sum_{i=1}^n w_i}, }[/math]

where we first find the "weight" of the value by inverting the square of the uncertainity...

[math]\displaystyle{ w_i = \frac{1}{\sigma_i^2}. }[/math]

this is done in my excel worksheet whose results are displayed above.

Therefore, my final weighted results for the value of plancks constant is...

where h is in eV*s and Wo is in V.

The accepted value of h is 4.136E-15 eV*s.

And the percent error of my value to the accepted value is...

[math]\displaystyle{ \delta = \frac{|v_{\text{approx}}-v|}{|v|}\times{}100. }[/math]

=3.6%