User:Johnsy/Lipoprotein Modelling/Model Analysis

Model Analysis

De Novo Synthesis Pathway and Degradation

Let us start by considering a simple system taking into account only cholesterol synthesis from HMG-CoA and it's degradation to either bile acids, steroid hormones, or other cholesterol derivatives. We can also model the action of statins as a competitive inhibitor of the enzyme HMG-CoA reductase, the main limiting enzyme of cholesterol biosynthesis. One of the key assumptions that is made is that the level of enzyme is constant (quasi-steady state approximation). Although this does not hold due to the genetic component, we will investigate the use of delay differential equations when considering a further extension to the model.

The equation we first consider is: [math]\displaystyle{ \frac{d[IC]}{dt} = \frac{V_1[H_0]}{K_{m1}+[H_0]+\frac{k_{m1}}{k_{i1}}[Statin]} - d_{ic}[IC] }[/math]

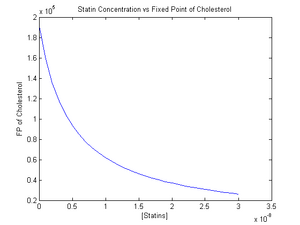
Solving for the fixed point of the equation is straightforward and we are left with the following steady state transfer function. [math]\displaystyle{ [IC]* = \frac{V_1[H_0]}{d_{ic}(K_{m1}+[H_0]+\frac{k_{m1}}{k_{i1}}[Statin])} }[/math]

The parameters in the equation are shown below with their approximate values and references.

1. V₁ - The V_max rate for HMG-CoA reductase, [math]\displaystyle{ 64 \times 10^{-9} M }[/math] (Theivagt)
2. K_m1 - The michaelis-menten constant for HMG-CoA reductase, [math]\displaystyle{ 20 \times 10^{-6} M }[/math] (Theivagt)
3. K_i1 - Dissociation constant for average statin, [math]\displaystyle{ 1.9 \times 10^{-9} M }[/math] (Flambers)
4. d_ic - Degradation rate of cholesterol, estimated [math]\displaystyle{ 2 \times 10^{-4} min^{-1} }[/math]
5. H₀ - Average amount of HMG-CoA in the cell, assumed constant, [math]\displaystyle{ 30 \times 10^{-6} M }[/math] (Corsini)

The graph in Figure 1 shows the effect of an increase in statin levels versus the steady state concentration of cholesterol.

Figure 1. Statin vs. Steady State Concentration of Cholesterol