User:Ginevra Cochran/Notebook/Physics 307L/Electron diffraction
Steve Koch 22:45, 21 December 2010 (EST):Good primary notebook, and looks like good measurements.
Purpose
The purpose of this lab is to study what happens when electrons act as waves and to attempt to verify the de Broglie hypothesis, as well as to measure the spacing of planes in graphite.
Safety
In this lab, as in most others, it is important to be careful around electricity and avoid touching frayed or ungrounded wires. In this lab, we were advised by the manual not to let the anode current exceed 25mA, but we had little control over this.
Equipment
- electron diffraction tube
- Wavetek 85XT digital multimeter
- Cabrera precision calipers
- BNC cables
- TEL 2501 universal stand
- 3B DC power supply (Model U3310)
Setup
We connected C5 on the universal stand to the negative on the HV supply. F4 went to the positive on the heater supply and the low voltage bias. G7 went to the positive lead on the HV supply, and we connected F3 on the universal stand to the negative on the heater supply.
Procedure
We switched on the main power supply after checking to be sure it was set to 0 volts, then switched on the low voltage bias. After waiting a few minutes for everything to heat up, we set our initial voltage to be 4kV, as this was the highest voltage we found we could reach without causing the graphite to glow. Using the calipers, we measured the diameters of the two rings that appeared on the phosphorus screen. We decreased our voltage by .1 kV and remeasured the inner and outer diameter, continuing this to 2.5kV, after which the rings became too difficult to discern clearly. We did this three times. At no point during a set of measurements did we find it necessary to adjust the trajectory of the beam using the magnet.
Data
{{#widget:Google Spreadsheet |key=0AqzpS6URre5adHNubHNZZXdqM1JBcjhod3JqQlZwMWc |width=750 |height=250 }}
Analysis
{{#widget:Google Spreadsheet |key=0AqzpS6URre5adFEwck9NXzgtS1JSUFhzZEtFZ0JnelE |width=750 |height=250 }}
The de Broglie hypothesis is [math]\displaystyle{ \lambda = \frac{h}{p} }[/math]
- The graphite lattice spacing can be found using the Bragg condition.
- [math]\displaystyle{ 2dsin(\theta) = n \lambda \,\! }[/math]
- For small angles, this relationship between the angle of diffraction and the length of the gun is [math]\displaystyle{ \frac{Rd}{L}=\lambda }[/math] where D is the spacing between the maxima on the screen.
- [math]\displaystyle{ \lambda = \frac{h}{p} = \frac{h}{\sqrt{2mE_{k}}}=\frac{h}{\sqrt{2meV_{a}}} =\frac{Rd}{L} }[/math]
Since [math]\displaystyle{ R=D/2 }[/math],
- [math]\displaystyle{ d=\frac{2hL}{D\sqrt{2meV_{a}}} }[/math]
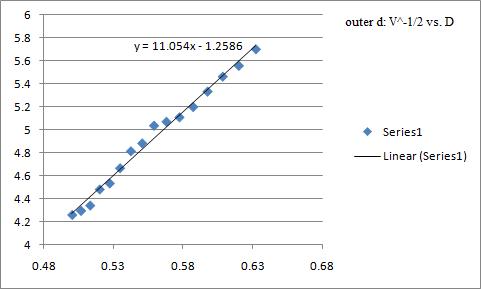
I graphed d versus [math]\displaystyle{ V^{-1/2} }[/math], and obtained fairly linear results, which support the de Broglie hypothesis.
inner d: V^-1/2 vs. D 
outer d: V^-1/2 vs. D
To correct for the thickness of the glass tube, we adjusted D to be
- [math]\displaystyle{ D_{new} = D_{obs} - 3mm*D_{obs}/2L \,\! }[/math], since the radius of curvature is 1.5 mm.
Since the electrons from the particle beam do not travel all of L, but only to the screen, we corrected L also.
- [math]\displaystyle{ L_{new} = L - 6.6cm*(1-cos(sin^{-1}(D_{obs}/2R)))\,\! }[/math].
Using a Google spreadsheet, I calculated the average values for [math]\displaystyle{ d_{inner}\,\! }[/math] and [math]\displaystyle{ d_{outer}\,\! }[/math].
- [math]\displaystyle{ d_{inner} = 0.19524 +/- 0.001 nm\,\! }[/math]
- [math]\displaystyle{ d_{outer} = 0.11153 +/- 0.0006 nm\,\! }[/math]
Error
Calculating the percent error against the accepted values [math]\displaystyle{ d_{inner} = 0.213 nm\,\! }[/math] and [math]\displaystyle{ d_{outer} = 0.123 nm\,\! }[/math].
- [math]\displaystyle{ \% error=\frac{d_{inner}-d_{measured}}{d_{inner}}\,\! }[/math]
- [math]\displaystyle{ \% error_{inner} = 8.34 %\,\! }[/math]
- [math]\displaystyle{ \% error_{outer} = 9.33 %\,\! }[/math]
The error in this lab was probably incurred by inaccuracy in measuring the diameters as they grew fuzzier, as opposed to due to calculation.
Sources
Cristhian Carrillo was my lab partner for this experiment. I referenced Professor Gold's manual. My photos are from Alex Andrego's lab notebook.
