User:Emran M. Qassem/Poisson
Overview
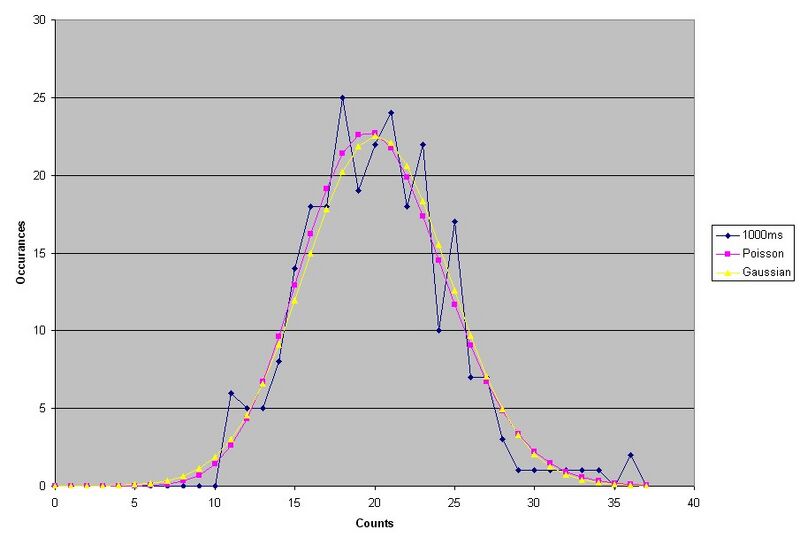
In this lab, we measured how much background radiation we get per time interval X and break each amount into bins and count how many times we find a "X interval" that fits into that "bin". Plotting this gives us a Poisson distribution. This will help us better understand the Poisson distribution and how it compares with a Gaussian distribution.
Procedure
We used a software provided to us on the computer and set it up to the recommended settings as explained in the lab manual and let it run collecting the data. We saved the data to files and imported the data into Microsoft Excel. We then plotted the data and plotted Poisson curves against our data. In the last graph where we had a much larger intervals which made the Poisson pretty much the same as the Gaussian. The equations we used:
- Poisson function:
- [math]\displaystyle{ \Pr = \frac{e^{-\lambda} (\lambda)^k}{k!} }[/math]
- Gaussian function:
- [math]\displaystyle{ f(x)=\frac{1}{\sqrt{2 \pi \sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}},\,\! }[/math]
- [math]\displaystyle{ f(x)=\frac{1}{\sqrt{2 \pi \sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}},\,\! }[/math]
Results
Our graphs and data had the general trend of the Poisson distribution, but were very jagged.
Error
The jaggedness of our data is a result of the number of channels we were using. Since we only used 256 channels, we did not get a lot of data points, thus resulting in data that looks to be far off from the Poisson distribution. If we had used a larger number of channels, as other lab groups had done, we would have got graph that had less error.
Conclusion
In this lab, I learned that the Poisson distribution is the same as a Gaussian distribution, just with the center shifted to the left, as the majority of data points occur close to 0, and you cannot have negative occurrences. I also saw from this lab that using 256 channels, much less than other lab groups, showed us how the distribution behaves and that it is not just a function, but it is a property of measuring data.