User:Emran M. Qassem/FormalReport
Using an Oscilloscope to Measure the Flight Time of Light
Auther: Emran Qassem
Email: eqassem@unm.edu
Experimentalists: Emran Qassem and Randy Lafler
University of New Mexico Physics Department
Undergraduate
Abstract
Attempting to measure the speed of light using a time of flight method with a light emitting diode, sending the light through a cardboard tube with a photomultiplier tube at the other end to detect photon arrival, we used an oscilloscope to measure the transmit signal and the arrival signal. The time difference measured and varying the distance between the transmitter and receiver gave a slope that represents the speed of light. Using the least squares method to find the slope, we have measured the speed of light to be 26.8 (7) cm/ns, which is in poor agreement of the accepted value. This implies there must be some systematic error or some fault in our measurement methods.
Introduction
The speed of light is a universal constant that we use in many calculations. Its constancy is key in explaining the Theory or Relativity. Michelson’s experiments to show the existence of Ether were the starting point for Einstein’s theory of relativity.[1] The speed of light has been measured many times with many different methods such as using a laser and measuring frequency and wavelength. [2] We are quite sure of its value to an accuracy of 299,792,458m/s.[3] The time of flight method has been done as well using a time to amplitude converter (TAC) as described in professor Gold’s lab manual, but has the problem of time walk.[4] Having found an oscilloscope that had the ability to measure down to 2 nanosecond resolution, we attempted to measure the speed of light without a TAC, thus eliminating time walk. If we had come up with good results, we could have possibly found a better method for measuring the speed of light than the TAC method.
Methods and materials
-
Figure 1: PMT: Photo Multiplier Tube.
-
Figure 2: PMT Connectors: This is the back of the PMT showing the connectors. The red is for -2000 volt power, the thinner wire is ground, the and the thicker wire is the signal.
-
Figure 3: -2000 volt power source: This is the TAC (time to amplitude converter) but it also has the -2000 volt source in it which powers the PMT.
-
Figure 4 Cardboard Tube: This is the inside of the tube looking in from the LED side, showing the meter stick which is attached to the LED.
In this experiment we used the a cardboard tube of approximately 5 meters in length (figure 4), a 200 volt power source (Harrison Laboratories Model #6207A 0-160 Volts/ 0-0.2 Amps) connected to an LED (photon emitting diode) attached to the end of a meter stick, a -2000 volt power source (EG&G Ortec Model 567 Time-to-Amplitude Converter/Single channel Analyzer, figure 3) connected to the PMT (Nano N-134 Photo Multiplier Tube), and a high resolution oscilloscope capable of measuring and displaying 2 nanosecond time differences.
We placed the PMT into one end of the cardboard tube connecting the appropriate BNC wire for -2000 volt power (red wire), ground (short connector wire), and signal (long connector thick wire, figure 1,2,3). We connected the signal wire to channel one of the oscilloscope. On the other end of the cardboard tube, we attached a few meter sticks together (for at least 4 meters of length, Figure 4) and attached the LED to one end of the meter sticks. On the LED, using BNC wires, attached 200 volt power and ground, as well as the signal BNC wire. The signal wire was attached to channel 2 of the oscilloscope.
We pushed the meter sticks all the way in so that the PMT and LED were almost touching. We powered on the 200 volt power supply, then the -2000 volt power supply, then the oscilloscope. We then adjusted the oscilloscope to 2 nanosecond separation and adjusted the trigger to go on the spike of the LED signal. We set the oscilloscope to average. We rotated the PMT so that we got the largest amplitude signal. We set up vertical measure bars on the oscilloscope so that we could measure the time difference between the LED signal and the PMT signal. We put the LED signal measurement line at the peak of the signal and left it there. The PMT signal measurement line was placed at the initial downward slope of the peak. We noted the current distance and the time difference.
In an attempt to find the best method, we ran the experiment 3 different ways. In the first method, we pulled the meter sticks out a distance of 50cm each time for 6 times for a total of 7 measurements, leaving the oscilloscope and PMT position the same, and adjusting the PMT downward slope line measurement on the oscilloscope to gather the time difference. We took these measurements a total of 3 times, pushing the meter sticks in, then out, then in.
In the second method, we did the same procedure, except we attempted to keep the peak of the first shelf of the PMT signal on the oscilloscope at the same visual amplitude by rotating the PMT to max intensity and then adjusting the oscilloscope voltage resolution so that the peak appears visually to be at the same place.
In the third method, we did the same procedure, as in the first and second methods, except we attempted to keep the peak of the shelf of the pmt signal on the oscilloscope at the same visual amplitude by adjusting the oscilloscope voltage resolution as well as rotating the PMT to lower the intensity.
Results and Discussion
To calculate the speed of light from our data, we fit a line to the data points using the LINEST Excel function (least squares, Table 1, Figure 5, 6). The slope gives us the value for the speed of light which we calculated. We did 5 trials, the first 3 with the same method, all resulting in similar values of 24 (1) cm/ns, 23.2 (7) cm/ns, and 24 (1). All of these values are much lower than the accepted value of 30 cm/ns for the speed of light. There must have been some kind of systematic error or fault in the way we were doing our measurements. In an attempt to correct this, we tried a slightly different method as described above. In trial 4, keeping the amplitude at maximum for the PMT and adjusting the oscilloscope so that the curves amplitude looks almost the same visually every time was an attempt to make our measurements the same each time as we were using the beginning of the downward slope of PMT signal to measure the time difference. We could not keep a visual representation on the oscilloscope that looked exactly the same every time because the maximum intensity changed as the LED traveled further away. The results we got were a little bit better, but still off by 4 sigma from the accepted value. In trial 5, we started with the LED all the way at 300 cm away, and adjusted back. We started with the PMT intensity at maximum by rotating it, and then adjusted the oscilloscope voltage resolution as well as reducing the PMT intensity to make the PMT signal appear to be exactly the same visually every time. This time we were able to keep the PMT signal curve looking exactly the same, but we lost a lot of intensity. The results were less than satisfactory at 35 (1), 5 sigma away from the accepted value.
All calculations and graphs are done in Microsoft Excel 2003: Speed of Light 2 XL Doc
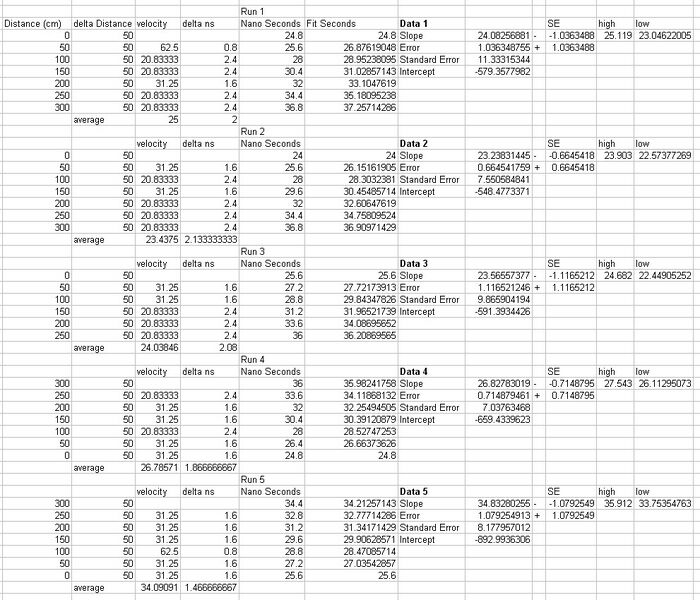
- Table 1 This table shows all the data we collected as well as the calculated values and error. The distance column represents the position of the LED with respect to the PMT. the delta distance column is the change in distance between one measurement and the next. The Nano seconds column represents the time measured on the oscilloscope between the LED signal pulse and the PMT signal pulse. The delta ns column represents the nanoseconds between the previous time measurement and the next time measurement. The Velocity column is just a simple calculation of change in distance divided by change in time.
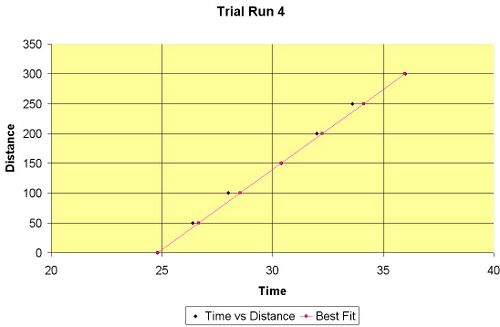
- Figure 5 This is the graph of the 4th trial.
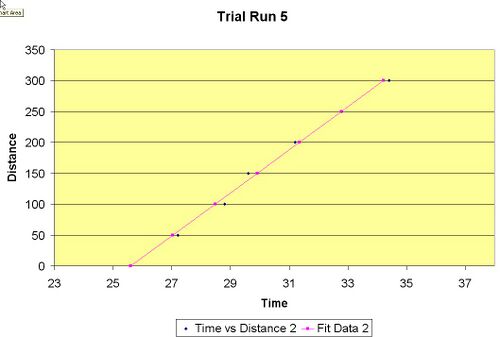
- Figure 6 This is the graph of the 5th trial.
Conclusions
The accepted value of the speed of light is 30 cm/ns and our best value is 26.8 (7) cm/ns. Off by 4 sigma, this is a poor result. This implies there is some systematic error or that our method of measuring is faulty. We noticed that the 4th and 5th trials are below and above the accepted value. This draws me to conclude that the amplitude and measurement method is very important in finding the time difference. When we were measuring the downward slope, we noticed that increasing the voltage resolution would make the beginning of the slope appear sooner. Also, the signal was being averaged, as there was a lot of noise and many little spikes at throughout the curve. This causes me to believe that as the intensity of the PMT signal and thus the amplitude on the oscilloscope caused the appearance of initial downward slope to change a little bit, therefore causing our measurements to be faulted by systematic error. Therefore, if we had instead used half max for the PMT signal curve, we might have got better results.
Acknowledgments
I thank Randy as I could not have done this without his help as my lab partner. I would also thank Dr. Koch for his instruction and for the idea of doing the experiment this way. I also thank Jesse Smith for an excellent example of a formal report.
References
- Holton, Gerald “Einstein, Michelson, and the ‘Crucial’ Experiment” Isis. Vol 60, No. 2 (Summer, 1969) pp. 132-197
- Evenson, M. K. "Speed of Light from Direct Frequency and Wavelength Measurements of the Methane-Stabilized Laser."" Quantum Electronics Division, National Bureau of Standards. (Sep. 11 1972) pp. 1-4. http://prl.aps.org/pdf/PRL/v29/i19/p1346_1.
- Codata http://physics.nist.gov/cgi-bin/cuu/Value?c
- Gold, Michael "Lab Manual" pp 65-71. http://www-hep.phys.unm.edu/~gold/phys307L/manual.pdf
- Smith’s Formal Report http://openwetware.org/images/4/4a/Jesse_Smith_Phys307L_Formal_Report.pdf



