User:Arianna Pregenzer-Wenzler/Notebook/Junior Lab/Electron Diffraction Summary
Electron Diffraction Summary
Purpose
In this experiment we are making use of the fact that particles (in our case electrons) have wave properties. Using a beam of electrons and the results of x-ray diffraction which showed that the diffraction pattern of x-rays through a lattice crystal could allow for the understanding of the way that the atoms in the crystal were spaced, we can use the Bragg condition for constructive interference, d*sinθ = mλ to determine the spacing between atoms in a graphite target.
Using the de Broglie relation between the wavelength of our electrons and their kinetic energy, which can be calculated from the accelerating potential of the electron beam, and relating the distance between the m=0 and 1st maxim (m=1) and the distance traveled by the electrons to sinθ we can experimentally determine distance d, the atomic spacing, using the following equation:
- d = 4*π*L*h/D*(2eV*m)
Results
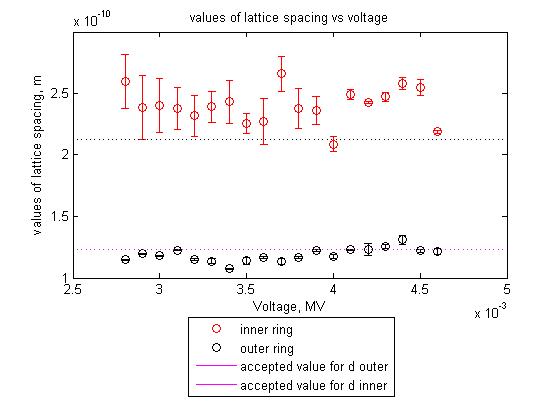
For graphite there are two different atomic spacings d which correspond to its lattice structure.
The accepted values of these spacing, as given by the lab manual are:
- d = .123 nm
- d = .231 nm
Using an average of the values of D measured at a voltage range from 4.6kV to 2.8kV, and computing d for each voltage and then taking the average d as my best guess with my error as the SEM I computed:
value from outer ring
- d = .118(30) nm
value from inner ring
- d = .24(24) nm SJK 03:05, 18 December 2008 (EST)

03:05, 18 December 2008 (EST)
I assume this is a typo? (the error is same as the value)
Both these values fall within the range of the accepted values with a 35% confidence interval, so on paper they look good, but the graphs tell a different story. My guess is that it would be pretty hard to get far from the accepted value for d using this particular apparatus, and making multiple trials.
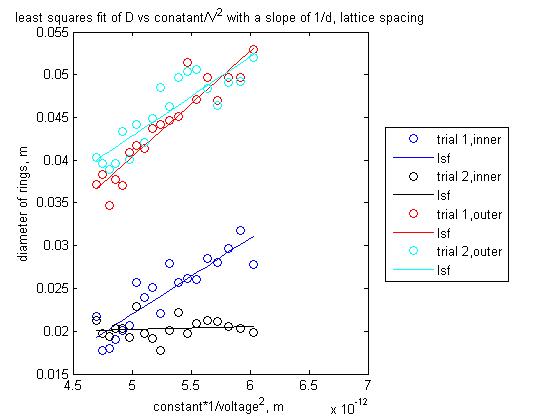
Using a least squares fit to calculate 1/d as the slope of D = constant*1/V^.5 I computed a value for d for each of two trials, with very poor results. I do not have error on these values for d, as I have not yet learned how to find them in matlab, and I did not go back and re-do the linear fit in excel, where I know how to get the error. Here are my calculated results, then I will let the graphs tell the story of the error.
SJK 03:10, 18 December 2008 (EST)

The graphs look really nice! I don't understand what these four values to the left indicate? d = 0? I think the problem with your linear fit is you should force it through the origin (i.e. no intercept) as Paul did, since there is no expected offset in the theory. This will produce better results and show the systematic error as well. I can't figure what happened with that data set that looks like it has no slope.
values from outer ring:
- d = .112 nm
- d = 0
values from inner ring:
- d = .081 nm
- d = .107 nm
Final Comments
I need to give credit to fellow student Paul Klimov, because I made use of his lab notebook for this lab as my initial source for theory. After reading Paul's notebook entry I followed up with my University Physics Text and the notes from my phys 262 class taught by professor Morgan-Tracy.SJK 03:08, 18 December 2008 (EST)

Good job giving credit here...Paul kicked some serious ass on this one.
Your first results above are entirely consistent with the accepted values, right? So why would you call the systematic error serious?
We had some serious systematic error in this lab probably due to an old electron diffraction tube, but despite poor experimental results I learned a lot from doing the data analysis and trying to get a better picture of the underlying theory.