User:Andy Maloney/Notebook/Lab Notebook of Andy Maloney/2010/01/19/Phase grating
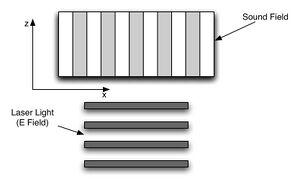
Phase grating
A plane wave electric field can be described as
[math]\displaystyle{ E=E_o\exp[i\beta] }[/math]
propagating in the z direction, where [math]\displaystyle{ \beta=\omega t-kz }[/math] is some phase and [math]\displaystyle{ E_o }[/math] is the amplitude of our electric field. Once the electric field passes through the chamber it will acquire another phase in the x direction due to the sound field's sinusoidally varying refractive index. Thus we have that the phase of the electric field coming out of the AOM looks like
[math]\displaystyle{ \beta=\omega t-kz+\frac{\phi}{2}\sin(k_sx) }[/math]
where [math]\displaystyle{ \phi/2 }[/math] is the amplitude of the acquired phase and [math]\displaystyle{ k_s=\frac{2\pi}{\lambda_T(\nu)} }[/math] is the wave number for the sound and [math]\displaystyle{ \nu }[/math] is the frequency of the sound wave. This gives us our new electric field exiting the AOM to be
[math]\displaystyle{ E'=E_o\exp\left[i\left(\omega t-kz+\frac{\phi}{2}\sin\left(\frac{2\pi}{\lambda_T(\nu)}x\right)\right)\right] }[/math]
This is pretty nasty. To try and reduce some of the complications, there is an expansion called the Jacobi--Anger expansion (Arfken) which states that
[math]\displaystyle{ \exp\left[i\frac{\phi}{2}\sin\left(\frac{2\pi}{\lambda_T(\nu)}x\right)\right]=\sum_{m=-\infty}^{\infty}J_m\left(\frac{\phi}{2} \right)\exp\left[im\frac{2\pi}{\lambda_T(\nu)}x\right] }[/math]
where [math]\displaystyle{ J_m\left(\frac{\phi}{2}\right) }[/math] is a Bessel function of the phase amplitude [math]\displaystyle{ \left(\frac{\phi}{2}\right) }[/math] and diffraction order [math]\displaystyle{ (m) }[/math]. Thus our electric field looks like (using the above expression)
[math]\displaystyle{ E'=E_o\exp\left[i\left(\omega t-kz\right)\right]\times\sum_{-\infty}^{\infty}J_m\left(\frac{\phi}{2} \right)\exp\left[im\frac{2\pi}{\lambda_T(\nu)}x\right] }[/math]
Remember that we are interested in the far field diffraction pattern. This means that we need to take the Fourier Transform of the electric field. Taking the Fourier transform with respect to x gives (after much simplifications)
[math]\displaystyle{ \tilde{E}=\left(\sum_{-\infty}^{\infty}J_m\left(\frac{\phi}{2}\right)\right)E }[/math]
What we see is the modulus squared of the electric field, so the intensity pattern you see in the far field should look like
[math]\displaystyle{ \eta(m,\phi)=\left|J_m\left(\frac{\phi}{2}\right)\right|^2 }[/math]
where again, [math]\displaystyle{ m }[/math] is the order of diffraction beginning at 0 not 1 due to the way the Bessel functions are defined, and [math]\displaystyle{ \left(\frac{\phi}{2}\right) }[/math] is the phase amplitude of the sound wave. This just means how strong the sound field is, or rather how loud it is.