User:Alex G. Benedict/Notebook/Physics 307L: Junior Lab/Speed of Light Lab
Speed of Light Lab
SJK 21:09, 25 October 2010 (EDT)
This is a pretty good primary notebook. Very nice data and spreadsheet. Good description of the analysis, I could follow what you did and was able to point out better avenues. The description of procedure could have been helped a lot, likely with the use of photos of the PMT signal, as noted below.
Note, I see now that Joe's notebook has more detail for the procedure, including photos, so that is good.
This lab was performed by myself and my partner Joseph Frye User:Joseph_Frye on September 27, and October 4, 2010. I would like to thank Brian Josey and Kristin Harriger, for their advice on data collection.
Set Up
There was actually not any set up required for this lab, since it was already assembled in the senior laboratory. For instructions on how to set up the lab see Dr Gold's manual, linked the last lab notebook or the Phys 307L website.
Equipment:
Tektronix Oscilloscope (Model TDS 1002)
Bertan Power Supply (Model 215, 3000V, 5mADC)
Canberra Delay Module (Model 2058)
Ortec TAC/SCA Module (Model 567)
Harshaw NIM Bin (Model NQ-75)
Harrison Laboratories Power Supply (Model 6207A, 160V, 0.2A)
Photomultiplier Tube (PMT)
LED circuit
Procedure
SJK 21:08, 25 October 2010 (EDT)
A picture of the PMT signal on the oscilloscope and a description of what feature(s) you were referencing and trying to keep constant would help a lot. This would be necessary for future reproducibility, I would think. As well as for discussing possible sources of systematic error.
The procedure for this lab consisted of starting the LED at some arbitrary distance from the photomultiplier, then moving it towards the photomultiplier at 10cm increments. Every time it was moved forward we tried to ensure that the oscilloscope was measuring about the same intensity for the light received by the photomultiplier tube by twisting the photomultiplier tube to adjust the angle of the polarizing filter.
On the first day we were keeping track of the distance from the PMT, and recording data using 25cm increments. On the second day we changed our procedure to work with arbitrary distances from the PMT. Instead of keeping track of the distance of the LED from the photomultiplier we just made note of the relative change in the distances, believing that the slope of the line is the most important part of the data since that should be the speed of light. The voltage measured is representative of the time it takes to reach the PMT. We know from the previous work of Josey and Harriger that the conversion factor of voltage to ns is 1V=10ns.SJK 20:10, 25 October 2010 (EDT)
This conversion factor will depend on the "range" and "multiplier" settings.
Data & Analysis
Here is the spreadsheet of the data. {{#widget:Google Spreadsheet |key=0AsLE8iWrtjlSdG55d1hPNVp1c20waXMtLXhEX3F5U0E |width=1200 |height=600 }}
SJK 21:06, 25 October 2010 (EDT)
Very nice data--great that you were able to take 10 very careful trials.
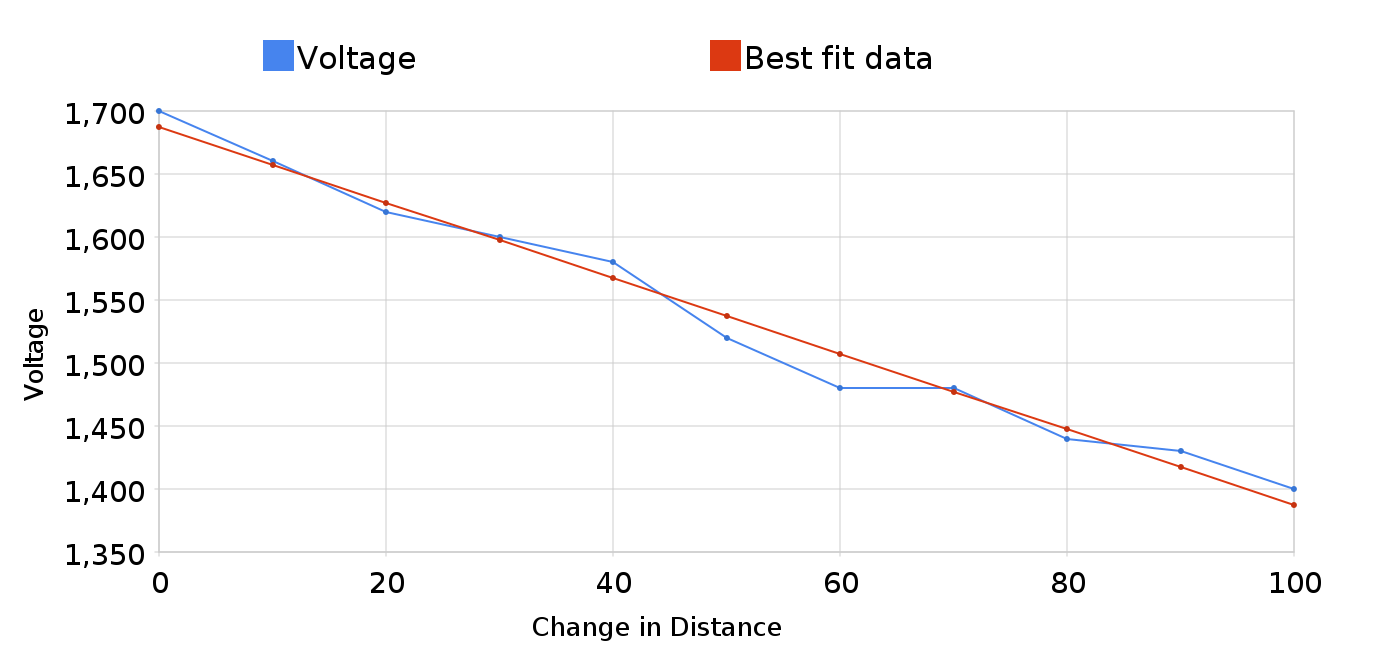
The data from the first day is not the best since we were recording too few data points for each trial, and were using a bad technique, it is plotted below vs the best fit line through the points.
The slope of the line in the picture is 0.20079999999999 +/- 0.1258206130436 which actually contains the speed of light(about 0.3 in those units) within the uncertainty. So we known with about 68% confidence that the speed of light is in the interval [7.4,32.59] cm/ns.
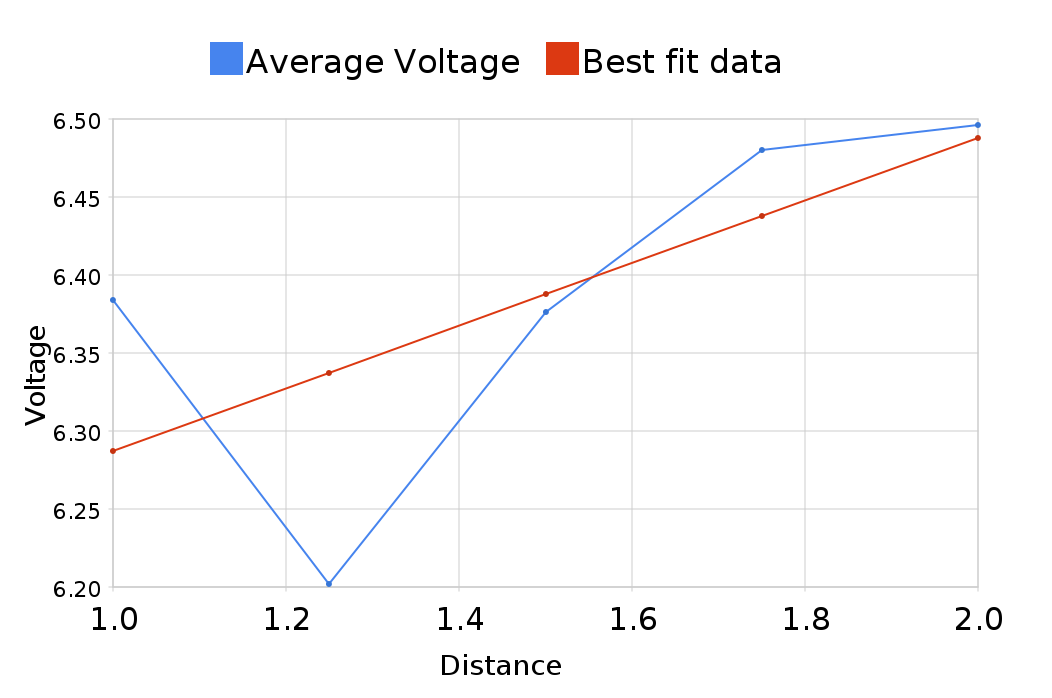
For the next day we changed our technique to be distance arbitrary. The data for this had lower uncertainty, since we were using more points. The average slope for this data was -3.26848484848484 +/- 0.24476146068253, where the uncertainty is taken to be the maximum of the the uncertainties of each fitSJK 21:03, 25 October 2010 (EDT)
As you probably realize now, saying the final uncertainty is equal to the most uncertain result does not correctly provide a 68% confidence interval. There are a couple routes you can go. One is to compute the mean of the slopes (as you do now) and the standard error of that mean. I think this gives you an uncertainty of .13 cm / ns. You could also compute a weighted mean and propagate the uncertainty using the formula we saw in class (total uncertainty = sqrt(1/sum(1/sig^2)). This gives a final uncertainy of .05 cm / ns and the weighted mean is slightly different at 3.25 cm/ns. However, at this point, you'd be presented with a puzzle: The individual measurements differ from each other by more than is expected from the uncertainty of the slopes. I don't know why, but it could be because the slopes seem more precise than they are, due to granularity of the voltage reading. Just a guess. At this point, I'd be inclined to use the SEM of the slopes and not do a weighted mean. So I'd report (3.27 +/- 0.13) cm/ns.
There's room for other arguments, but using the biggest individual uncertainty is not correct. Suppose you took that measurement first. Taking more data, you would only expect the overall uncertainty to decrease, not stay the same or increase.
The minus sign is irrelevant and comes from the fact that the distance from the LED to the PMT was decreasing, so with 68% confidence we know the speed of light is within the interval [30.24,35.13] cm/ns.
A sample plot from this day is given below for trial 8:
The actual value of the speed of light is 29.9792458 cm/ns
