The Benefits of Small Length Scales in Microscale Systems - Kush Basu
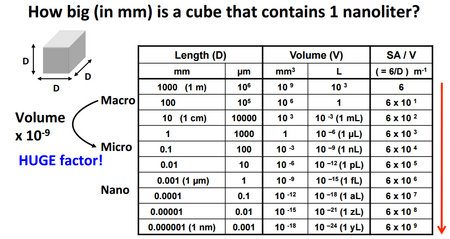
There are many different benefits to working on the microscale including making systems more portable, safer, cheaper, and quicker. Two of the most significant factors that are impacted by the difference between macro and micro length scales (seen in Figure 1) are heat and mass transfer in systems 1.
Actually knowing how easy it is to provide heat to a system or how fast the heat can be transported from the system is a huge parameter in determining the efficiency and safety of the process. For mass transfer, knowing how certain products will move within a system or between different streams is huge for determining the purity of systems and their effectiveness as well. These are both important phenomenons that occur when trying to make any system, however there are some distinct differences when going into the microscale.
Background
It is evident that on the microscale, the volume of the system is significantly smaller for smaller lengths considering volume is essentially the cube of a decimal number. The small volume limits the amount of mass in the system, which under the right conditions, is much easier to move. Also, as the volume decreases, the surface area to volume ratio increases drastically (Figure 1). Because heat transfer happens across the surface area, a greater surface area allows a much greater heat gain or loss throughout the volume of the system. As proven mathematically, the rates of heat and mass transfer increase drastically as length scale decreases to the point that even very slight changes in length lead to big changes in rate. Due to this large change in heat and mass transfer over small changes in length, very sharp heat and mass gradients form within microscale systems. There are numerous applications for these different gradients in research and industry based processes.
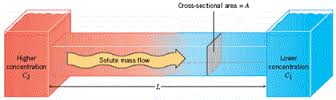
Mass Transfer
In a similar fashion to how significantly the rate of heat transfer is impacted by working on the micro scale, the mass flux of systems drastically increases as size decreases. This is governed by Fick’s laws of diffusion.
Fick's First Law
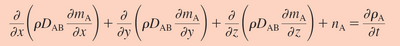
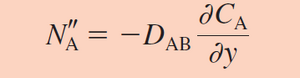
Fick's first law relates the concentration of a solute species to the diffusion flux of that species. This law states that the flux will move along a concentration gradient, from an area of high solute concentration towards one with a lower solute concentration. This concentration gradient is mathematically calculated as the partial derivative of solute concentration with respect to distance. Because distance is once again in the denominator of the governing transfer equation, working on the micro scale compared to the macro scale improves the transfer of mass exponentially. This gradient term is then multiplied by the diffusion coefficient which is specific for each system and conditions.
Heat Transfer
At the micro scale, the form of heat transfer that contributes most to the system is conduction. Conduction is the transfer of heat associated with diffusion of heat energy through random motion of molecules. The transfer occurs through the direct collision of molecules of higher energy with molecules of low energy. This from of heat transfer is possible due to the laminar flow profiles that exist at the microscale. Heat transfer also operates in a similar mechanism that mass transfer does, moving along a gradient. However here, the gradient is of temperatures rather than concentrations.1.
Fourier's Law
Conduction for any material is governed by Fourier’ Law. This is a constitutive equation relating the rate of heat transfer for an object to an intrinsic thermal conductivity coefficient as well as the temperature change and distance the conductivity occurs over. It is interesting to note that the conductivity coefficient k, which is an intrinsic transport property of a material, is generally used only for conduction in one direction (Figure 3) but is actually a tensor so it applies to heat transfer in 3 directions (shown in Equation 3) 2. Flow in traditional microfluidic devices is usually considered only in one or two dimensions, however more modern devices also make use of adding a third dimension to devices which is when the tensor aspect of the coefficient is utilized2. The application of using 3 dimensions for microfluidic devices are that it allows channels to split and cross over one another. This enables for such mechanisms as allowing one channel to be actuated by a valve on a separate level, leaving the second channel unaffected. Another use for 3-D microfluidic devices is for increasing the rate of passive mixing as a large curvature is sometimes required to mix fluids within a laminar profile.
Fourier' s Law:
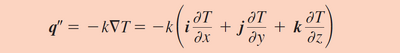
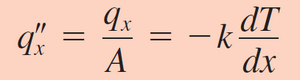
A simplified version of Fourier's law is used more often. Equation 4 relates the relation between heat transfer rate and heat flux as solved by Fourier's in one direction and at steady state.
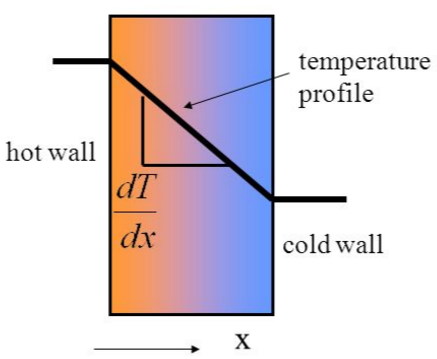
In the second equation, the important factor that relates to microfluidics is the x term in the denominator of the equation (Figure 3). For macroscale systems, such as pipe flow for factory sized reactors, the length scale is on the scale of meters. This means that the size of the system extremely limits macro scale systems. However, for microfluidic devices, which are devices ranging from 10-6 to 10-9 meters, the q value raises significantly with all other factors (i.e. the thermal conductivity coefficient of the material and the temperature difference) remaining the same. While there will be some changes in the conductivity coefficient and even the temperature change going from a macro system to a micro one, if those values were kept the same, scaling a system from being 10 meters to 10 microns would result in over a 6 fold increase in the rate of heat transferred.
Applications
Mass Transfer
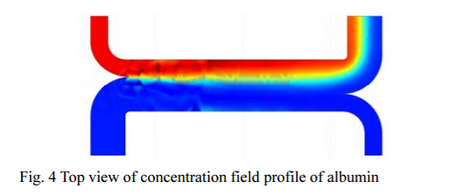
As shown above, by working on the microscale, not only is the rate of transferring mass across a system faster, but it can also be more finely tuned using the very large concentration gradients of these systems. A very cool example of this is the idea of using microscale devices as a means of separating components without using means such as adsorbents or membranes. An example of this that has been tested has been separating waste urea from blood without the use of membrane. The only way that this could even be possible is using a glomerulus microchannel, where the laminar flow profile prevents mixing between the blood and a solution of albumin, urea and glucose. The large molecule of albumin has difficulty traveling through the two fluids creating a concentration gradient. This allows almost all of the small molecules within the blood (namely Urea) to travel from the blood to the albumin mixture over a a very short length and very effectively 4. The actual gradient of albumin can be seen in Figure 4. Another application of a short msas transfer gradient in microfluidics is in protein crystallization and the use of counter diffusion (diffusion of two different species from opposite directions to come into contact) between the protein and precipitants. The only way to fine tune the gradients of both the protein and precipitate (which helps enable the crystallization of the protein to a certain extent) is through only through mass diffusion, without convective mixing and this is only possible at the microscale.
Heat Transfer
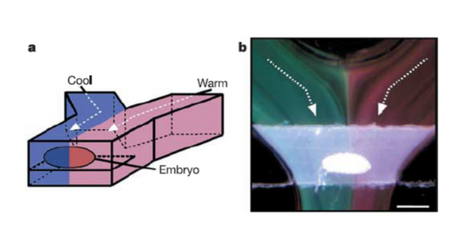
There are also several applications for high thermal gradients at the microscale. Because of the laminar flow profile of microscale systems, there is little mixing between fluids in straight/parallel channels. Because of this, it is possible to have a single hot stream and a cold one exist right next to each without a huge temperature gradient in between (due to the very small distance in between them). This allows for the testing of as single object, for example a fruit fly embryo to be simultaneously be applied to a hot temperature on one side and a cold temperature at the other, and to see the results these have on the embryo (Figure 5)5. Another huge application for the sharp temperature gradient of microsystems is the vitrification of protein crystals through cryo-cooling 3. In order to solidify protein crystals without deforming their structure in ice, it is necessary to essentially super-freeze water past the state of ice and into a glass-like state. To do this, the protein crystal in solution must be supercooled instantaneously and the only way to cool something that fast is with the incredibly high rate of heat loss that is characteristic in microscale systems.
References
1. Sun, Bing. (2015). Application of microfluidics technology in chemical engineering for enhanced safety. Process Safety Progress. 35(4), 365-373. http://onlinelibrary.wiley.com/doi/10.1002/prs.11801/pdf
2. Bergman, Theodore L., Lavine, Adrienne S., Incropera, Frank P., Dewitt, David P. Fundamentals of Heat and Mass Transfer, 7th edition. (2012). John Wiley & Sons Inc.
3. E. Garman. (1999). Cool data: quantity AND quality Acta Crystallogr. D, 55, pp. 1641–1653. https://doi.org/10.1107/S0907444999008653
4. Lee, SJ. & Choi, BK. Int. J. Precis. Eng. Manuf. (2012) 13: 307. https://doi.org/10.1007/s12541-012-0039-x
5. Luchetta, Nature. 2005 Apr 28; 434(7037): 1134–1138. https://doi.org/10.1038/nature03509
