Surface Wetting - Jocelyn Yuen, Chris Ortins

In microfluidics, surface tension is a useful force that is used to drive flow in below sub-millimeter ranged devices. At this size, the effects of surface tension begin to dominate classical mechanics and can overcome Newtonian forces such as gravity and inertia[1]. This characteristic allows surface tension to govern some flows at this scale.

In many microfluidic devices, however, the use of microvalves including macro devices and machines used to actuate and control the flow behavior throughout the device still provide practical issues. Some of these complications include the need to utilize magnetic, mechanical, and pneumatic systems to control flow, increasing the size and costs of the overall integrated device[2]. More recent methods have been taking advantage of the enhanced surface tension properties in microfluidics as an alternative to control flow in these devices. The high surface-to-volume ratio of these devices make surface properties of these channels critical to controlling flow behavior[2]. By adjusting some of these surface properties, the ability to control flow without a means of mechanical materials may be used to control interfaces by creating a gradient in hydrophobicity[6]. Some examples of methods to modify the surface of the channels include self-assembled monolayer (SAM) chemistry, absorption of polymers, multistream liquid laminar flow, photolithographic methods, and plasma treatment[2].

Example of different surface properties in microfluidic channels (a) Microfluidic device fabricated with cyclic olefin copolymer (COC) without any surface treatment (b) COC channel where surface is coated with TiO[5] film creating a hydrophilic surface [3]

Surface Wetting

Surface wetting is described by a liquid's ability to spread across a solid surface depending on the intermolecular interactions between the two states¹. When considering molecules located in the bulk at a condensed state, these molecules are attracted to each other by interactions such as van der Waals forces or polar hydrogen bonding. In comparison to the molecules along the interface of the condensed phase with a secondary phase, these molecules experience half the attractive forces as the ones described in the previous scenario. As a result, a local dissymmetry is experienced by the molecules at the interface and causes a disturbance in the surface energy. Consequently, fluids will always act to minimize the surface area of the interface to rebalance the cohesive energy of the system. This also means that energy is needed when increasing an interfacial area. At the macroscopic scale, surface tension is the physical quantity used to describe this molecular effect and can be estimated by the cohesive energy that keeps molecules attracted to each other[5].

[math]\displaystyle{ \gamma \approx \frac {U}{2 \delta^2} }[/math]

where [math]\displaystyle{ \gamma }[/math] is the surface tension referring to two components on each side of the interface, [math]\displaystyle{ U }[/math] is the total cohesive energy per molecule, [math]\displaystyle{ \delta }[/math] is a characteristic molecular dimension, and [math]\displaystyle{ \delta^2 }[/math] surface area of that molecule. Surface tension may also be identified with surface energy which is the energy needed to increase the surface area by one unit [4].

Interfacial tension also appears between other two phases such as liquid/gas interfaces or liquid/liquid interfaces when the two fluids are immiscible. The dissymmetric energy between two fluids is usually less. With an addition of a solid surface with two fluid phases, a contact angle may be formed at the intersection of the three phases and is a useful characteristic of surface wettability [4].

Spreading parameter depiction of surface wetting where surface experiences (A) partial wetting (B) total wetting (C) complete dewetting [4]

Partially wetted surfaces: where the contact angle is less than 90° (hydrophillic surface) and the contact angle is more than 90° (hydrophobic surface) [5]

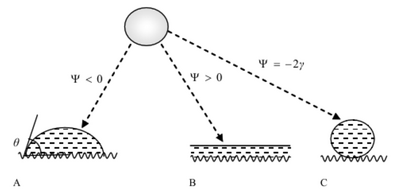
Spreading Parameter

The concept of wettability due to the interactions between particles has been defined by Thomas Young and can be understood by looking at two static scenarios of a droplet on a surface: either the drop will spread completely over the surface or form a cap as shown in the figure to the left. This phenomenon is dictated by the spreading parameter[4]:

[math]\displaystyle{ \psi = \hat{G}^*_{SA} - (\hat{G}^*_{SL} + \hat{G}_{LA}) }[/math]

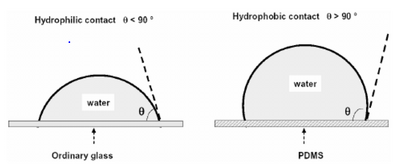
where [math]\displaystyle{ \psi }[/math] is the spreading parameter, Ĝ*_SA and Ĝ*_SL are specific energies at the rough solid/air and solid/liquid interfaces respectively, and Ĝ*_LA is the specific energy at the smooth liquid/air interface, also known as [math]\displaystyle{ \gamma }[/math]. When [math]\displaystyle{ \psi \gt 0 }[/math] the surface experiences total wetting and the liquid completely spreads to lower its surface energy. When [math]\displaystyle{ \psi \lt 0 }[/math] the droplet sticks to the surface with partial wetting. A contact angle develops between the solid surface and the liquid/air interface where [math]\displaystyle{ \theta \gt 0 }[/math]. In partial wetting scenarios, when the contact angle is [math]\displaystyle{ \theta }[/math] < 90° the surface is said to be hydrophillic and when the contact angle is [math]\displaystyle{ \theta }[/math] > 90° the surface is said to be hydrophobic. In the most extreme situation where [math]\displaystyle{ \psi = -2\gamma }[/math], the surface experiences complete dewetting or superhydrophobicity [5].

In application to microfluidics, PDMS (silicone) is typically hydrophobic while glass is hydrophilic. Both of these are typical substrates used in microfluidic devices.

Main radii of curvature depicting laplace overpressure [4]

Surface patterning of a microfluidic channel where both hydrophilic and hydrophilic surfaces are created [9]

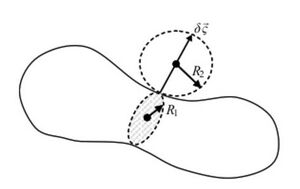
The Laplace Pressure

Surface tension causes overpressure in droplets and bubbles [4] and is related to the curvature of the interface[5]. This is described in Laplace's formula:

[math]\displaystyle{ p_L = \gamma (\frac{1}{R_1} + \frac{1}{R_2}) }[/math]

where p_L is the overpressure from media 1 to 2, [math]\displaystyle{ \gamma }[/math] is the interfacial tension, and R₁ and R₂ are the main radii of curvature of the surface at a certain point.

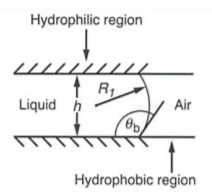
Consider surface patterning a microfluidic channel with two SAMs of trichlorosilane were used to create one hydrophilic surface and one hydrophilic surface. When a liquid stream is introduced into the microchannel, the water surface creates a curved liquid/gas interface and a pressure drop is induced due to surface free energy. According to Laplace's law, the concave side of an interface always has a pressure greater than the convex side. This characteristic of surface tension and curvature at interfaces allow control in flow in microfluidic devices [9].

The Marangoni Effect

The Marangoni Effect is the migration of aqueous solutions along a solid or viscous medium from a high to low solid-liquid interfacial potential [8]. Marangoni flow makes use of this potential to control flow through a microchannel [7] and is induced by creating a gradient in surface tension to drive flow from a locally smaller value of surface tension to a locally higher value of surface tension [8]. Applications of Marangoni flow has thus been useful in microfluidics as flow has proven to be controlled by constructing gradients by temperature means, electrical means, or chemical means to derive the gradients in surface tension. Ferrocene surfactants, for example, are used to generate a localized excess charge on the surface allowing interfaces between two immiscible electrolyte solutions (ITIES) to experience a capillary action and flow along a microchannel[7].

Thermalwetting

Surface tension values are dependent on temperature and can be described by Eötvös rule [4]:

[math]\displaystyle{ (V_{ML})^{2/3}\gamma = \hat{k}(T_C - T) }[/math]

where [math]\displaystyle{ V }[/math]_ML is the molar volume of the liquid, [math]\displaystyle{ T }[/math]_C is the critical temperature of a liquid, and k̂ is the Eötvös constant which is equal to 2.1×-7 [math]\displaystyle{ \frac{J}{mol^{2/3}K} }[/math].

As temperature increases, the kinetic energy of the molecules increases detracting the energy away from cohesive forces. Thus, surface tension typically decreases with increasing temperature which is also a phenomenon called the Marangoni convection or thermocapillary instabilities. Upon locally heating and locally cooling along the ends of an interface, a surface tension gradient can be induced to move fluid from warmer regions to cooler regions. Thus an external source of heating systems in microfluidics may be used to drive droplets through microchannels [4].

Schematic of an electrowetting display model where M is two sections of metal, E is a liquid electrolyte, A is a gas phase, I is an insulator, V₁ and V₂ are voltage sources, and L are nonwetting ends to keep the electrolyte in the capillary. [8]

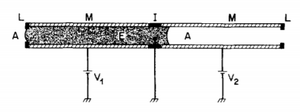
Electrowetting

By electrically altering a surface and creating a surface tension gradient, a liquid can be moved and controlled in a microfluidic channel. The surface tension modulation is created when there are an ionic conductor and an electric conductor at the interface. In electrowetting, an applied voltage is used to alter the surface tension of the system. Such an electric wetting display can be modeled in device considering two metallic capillary sections, M, separated by an insulating region "I". The two metallic regions are connected to two voltage sources, "V"₁ and "V"₂ which can control the motion of a liquid electrolyte inside the capillary. Both ends of the electrolyte must be inhabited by another phase such as gas or air, "A", and a potential difference between the two metallic sections can be altered to adjust the interfacial tension. With enough electric potential, a pressure gradient in the electrolyte will induce flow movement in a channel[8].

Schematic of Marangoni convection induced by a concentration gradient[5]

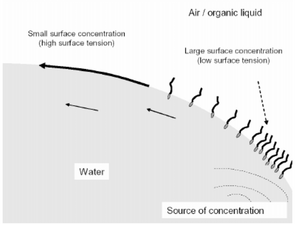
Surfactants

Surfactants can also be used to modify surfaces to change the surface tension between the two interfaces. Since surfactants are amphiphilic in nature, they tend to stick at interfaces with their hydrophilic heads attracted to more polar phases and their hydrophobic tails attracted to more organic phases. As the concentration of surfactants increases, the number of surfactant molecules at the interface becomes more saturated also decreasing the surface tension. Thus a Marangoni flow may also be induced upon creating a concentration gradient along the surface of microfluidic channels[5].

Microfluidic Interfaces

Applications of microfluidic interfaces including (a) Floating Interfaces (b) Pinned Interfaces (c) Moving interfaces (d) Secondary Interfaces[6]

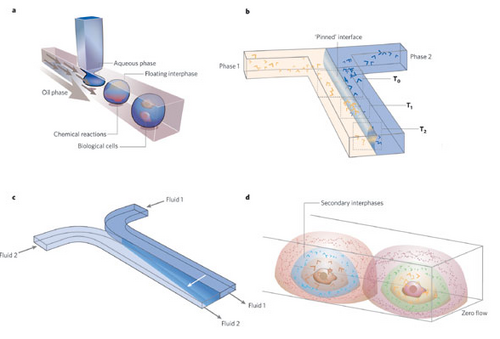
Surface tension provides unique interfacial behaviors and fluid control in microfluidics. Some examples include³:

• Floating Interfaces

Consider two immiscible fluids where droplets of one are immersed in another. This creates a floating interface which may act as a semipermeable container wall

• Pinned Interfaces

Two immiscible fluids flowing next two each other in a microchannel where their contact creates a pinned interface and may act as a membrane

• Moving Interfaces

Two miscible fluids flowing next two each other in a microchannel where diffusion between the two causes controlled mixing and an apparent moving interface

• Secondary Interfaces

Consider a concentration of solute in a droplet with no flow. Diffusion of the solute may create a secondary interface within the droplet providing may functional roles

Surface Wetting Applications

Wetting Morphologies at Microstructured Surfaces

Being able to efficiently work with small amount of liquids is an integral skill in industries including biomedicine and molecular biology. This study uses open microfluidic systems which have free liquid/vapor interfaces because these systems have the advantage of being more accessible and easier to clean. The focus of the research is the filaments that develop in the grooves and their geometry that can remain constant throughout the length of the groove. The certain morphologies were were obtained by matching surface topography and wettability by using two parameters: the aspect ratio (X) of the groove geometry and the contact angle (θ). The liquid/ vapor interfaces that dictate the shape of the liquid re characterized by the mean curvature, M, and contact angle. The mean curvature is found using the interfacial tension, Σ, and Laplace Pressure, P_La, using the Laplace equation: 2MΣ = P_La¹⁰

Sideviews of wetting morphologies in surface grooves with rectangle cross-sections. The top row shows substrates with contact angles above 45°, while the bottom below 45°. The top row shows the liquid forming corner droplets (cD), pinned droplets (pD), overspilling droplets (D), and extended filaments F). The liquid forms corner wedges (cW), pinned wedges (pW), overspilling droplets with pinned wedges, and filaments with pinned wedges when the contact angle is below 45° [10]

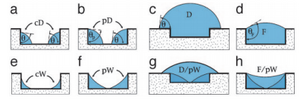
PDMS Microfluidic Channels

Surface wetting can be use to create microfluidic channels of desired quality. An experiment was done to create cylindrical PDMS channels with tangential chord angles (TCAs) close to 90° by exploiting support materials and varying their surface contact angle (SCA). The TCA is final angle of the solid channel while the SCA amounts to the angle θ involved in the Young's relation for a liquid in air¹³:

Cross-section of a channel wear a is the tangential chord angle, W is the width of the hydrophilic green domain compared to the hydrophobic purple domain. The grey on the bottom is the supporting material with the light blue showing the final channel. [13]

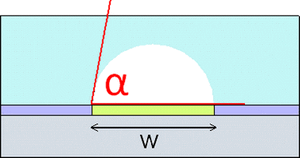
[math]\displaystyle{ cos(\theta) = \frac{(\gamma_s − \gamma_{sl})}{\gamma_{lv}} }[/math]

a. Method one with aqueous solution in the middle of two PDMS strips coated with CHF₃. The aqueous center component creates a channel definition then PDMS is poured in to create. the channel. b. The second method uses a shadowmask and degradation to create the hydrophilic/hydrophobic contrast, thus allowing the aqueous salt solution to form channel definitions in the degraded OTS where the PDMS is poured over to make the channels [13]

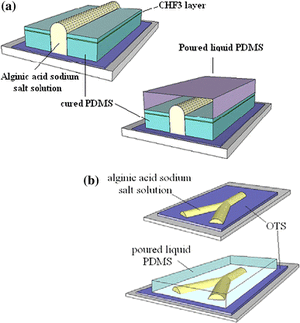
γs denotes the surface tension of the solid surface, γsl is the solid-liquid surface tension, and γlv is the liquid-vapor surface tension. The creation of these channels was based on optimizing the wetting parameters. The optimization created hydrophilic and hydrophobic steps to create the channel pattern definition with alginic acid sodium salt aqueous solution. The first method uses PDMS coated with CHF₃ on a silicon wafer. The PDMS is cut in strips with the middle taken out and the alginic acid sodium salt aqueous solution is poured in the middle. Since the hydrophilic aqueous solution does not spread to the hydrophobic strips, the channel definition is formed and PDMS is then poured over the top to create the channel. The second method uses octadecyltrichlorosilane (OTS) coated surface that is degraded with UV and O₃. A shadow mask is used to cover the OTS surface except for the places to be degraded to create a hydrophobic/hydrophilic contrast, which allows for more complex channels. After the OTS surface is degraded the aqueous salt solution is poured and created channel definition on the degraded OTS. Results showed that the first method was more effective with TCAs up 70°, while the second method sees its best channels with TCAs of only 55°¹³.

Thermal-Responsive Anisotropic Wetting Microstructures for Manipulation of Fluids in Microfluidics

PNIPAAm-modified Si stripes on silicon slides were made as substrates for manipulating the flow motion of fluid on a chip. PNIPAAm is a thermally responsive polymer which can be used to dictate the flow of a fluid. The polymer has a lower critical solution temperature and when the temperature of the system goes above and below this temperature the wettability of the liquid switches between strong and weak anisotropy. The flow in the microchannels was both anisotropic and isotropic at different times with different temperatures. The three parameters that influenced the thermal-responsive flow motion are applied pressure, the thickness of the polymer, and the dimensions of the microchannels. This study concluded that this system could be used as a thermal-responsive microvalve after applied pressure tests were conducted, the system temperature was able to be tuned, and the assistant gas was added. This technology could be used in many practical biomedical practices including immunodetection and protein analysis¹¹.

Thermal-selective valve function showing anisotropic (red) flow and isotropic (blue) flow at different times and temperatures [11]

Effect of wetting on capillary pumping in microchannels

Being able to control flow in a microfluidic system is very important and one way liquid moves in these small spaces is the difference in Laplace pressure. If two drops with the same contact angle in a channel the smaller drop has a greater Laplace pressure since it is defined by the liquid-vapor surface tension divided by the radius of the drops curvature. However, wetting properties can be manipulated using two parameters, radius of contact line (R_w) and contact radius (θ), if the drops are spherical caps and the pressure can be calculated using this equation¹²:

[math]\displaystyle{ \frac{2\gamma}{R_w} sin(\theta) }[/math]

This equation allows for the potential of larger drops to flow towards small drops since the Laplace pressure is so dependent on the contact angle. If the contact angle of the large drop is close to 90° and a smaller drop has a smaller contact angle, then the Laplace pressure of the large drop would be larger and flow would be towards the smaller drop. Results were found by analyzing movies using a CCD camara at 125 frames/s. It was found that backflow occurred when there was a large difference in the surfaces under the drops and the pressure of the larger drop was larger than the pressure of the smaller drop. Since smaller initial contact angles of the smaller drops resulted in more backflow it was concluded that wetting properties can be used for active pumping¹².

Principle of electrowetting based lenses and applications to imaging

Optical parts are smaller than ever and when they are need in the 1-10mm range, manipulating liquid droplets may be an effective method of developing the lenses. The biggest obstacle facing these types of lenses is stabilizing the optical axis. Electrowetting is used for the liquid-liquid interface by changing the relative wettabilities of the liquids by applying a voltage. The densities of the liquids must be exact so any orientation of axis is possible and can be controlled by slightly changing liquid composition. The most important aspect of stabilizing the optical axis is centering the liquid drop, which was done using a dielectric thickness gradient as well as geometry. An equation for the contact angle of the oil drop on the planar surface, including the the insular film thickness (e) and dielectric constant is: cos(θ)=cos(θ₀)- 1/2 εε₀/(eγ)(V²). The results showed that the centering methods worked very efficiently. Stabilizing the optical axis can be done by centering the liquid-liquid interface and this type of lens could be used as an optical component of a more complex system¹⁴.

References

1. Went, F. W. The Size of Man. American Scientist. 1968, 56 (4), 400–413.
2. Wang, S.; Wang, T.; Ge, P.; Xue, P.; Ye, S.; Chen, H.; Zibo, L.; Zhang, J.; Yang, B. Controlling Flow Behavior of Water in Microfluidics with a Chemically Patterned Anisotropic Wetting Surface. "Langmuir", ""2015"", 31 (13): 4032-4039. http://dx.doi.org/10.1021/acs.langmuir.5b00328
3. Lee, J.; Kim, S. K.; Park, H.; Kim, T. S. TiO₂ coated microfluidic devices for recoverable hydrophilic and hydrophobic patterns. "Journal of Micromechanics and Microengineering" ""2015"", 25. http://dx.doi.org/10.1088/0960-1317/25/3/035032
4. Bormashenko, E. Y. Wetting of Real Surfaces; De Gutyr Studies in Mathematical Physics; De Gutyr: Berlin, 2013
5. Berthier, J.; Silberzan, P. Microfluidics for Biotechnology; Artech House Integrated Microsystems series; Artech House: Boston, 2010
6. Atencia, J.; Beebe, D. J. Controlled Microfluidic Interfaces. Nature, ""2005"" Sep 29; "437"(7059): 648-55 http://dx.doi.org/10.1038/nature04163
7. Lee, H. J.; Fermin, D. J.; Corn, R. M.; Girault, H. H. Marangoni Flow in Micro-channels. Electrochemistry Communications, ""1999""; "1"(5): 190-193 http://dx.doi.org/10.1016/S1388-2481(99)00038-7
Principals For Active Control of Liquids on Submillimeter Scales; Science: New York, 1999; 283(5398): 57-60
8. Tadmore, R. Marangoni flow revisited. "Journal of Colloid and Interface Science", 2009, 332(2), 451-454 http://dx.doi.org/10.1016/j.jcis.2008.12.047
9. Zhao, B.; Moore, J. S.; Beebe, D. J. Surface-Directed Liquid Flow Inside Microchannels. "Science", ""2001"", "291"(5506), 1023-1026 Stable URL: http://www.jstor.org/stable/3082289
10. Seemann, R.; Brinkmann, M.; Kramer, E.; Lange, F.; Lipowsky, R. Wetting morphologies at microstructured surfaces. PNAS. February 8, 2005. https://dx.doi.org/10.1073/pnas.0407721102

11. Yu, N.; Wang, S.; Liu, Y.; Xue, P.; Ge, P.; Nan, J.; Ye, S.; Liu, W.; Zhang, J.; Yang, B. Thermal-Responsive Anisotropic Wetting Microstructures for Manipulation of Fluids in Microfluidics. Langmuir 2017 33 (2), 494-502. https://dx.doi.org/10.1021/acs.langmuir.6b03896

12. Javadi, A.; Habibi, M.; Taheri, F.S.; Moulinet, S.; Bonn, D. Effect of wetting on capillary pumping in microchannels. Scientific Reports volume 3, Article number: 1412 (2013). https//dx.doi.org/10.1038/srep01412

13. De Ville, M., Coquet, P., Brunet, P., & Boukherroub, R. (n.d). Simple and low-cost fabrication of PDMS microfluidic round channels by surface-wetting parameters optimization. Microfluidics And Nanofluidics, 12(6), 953-961. https://dx.doi.org/10.1007/s10404-011-0929-8

14. Berge, B. Liquid lens technology: principle of electrowetting based lenses and applications to imaging. Micro Electro Mechanical Systems, 2005. https//dx.doi.org/10.1109/MEMSYS.2005.1453908