Stripe Formation Patterns
This page is contributed by Ton Subsoontorn
Example Patterns
Specifications
| Theoretical | Empirical | |
|---|---|---|
| Pixel Dimension | 25 ums | |
| Pattern Size | 100 ums | |
| Accuracy | ||
| Precision |
Mechanism
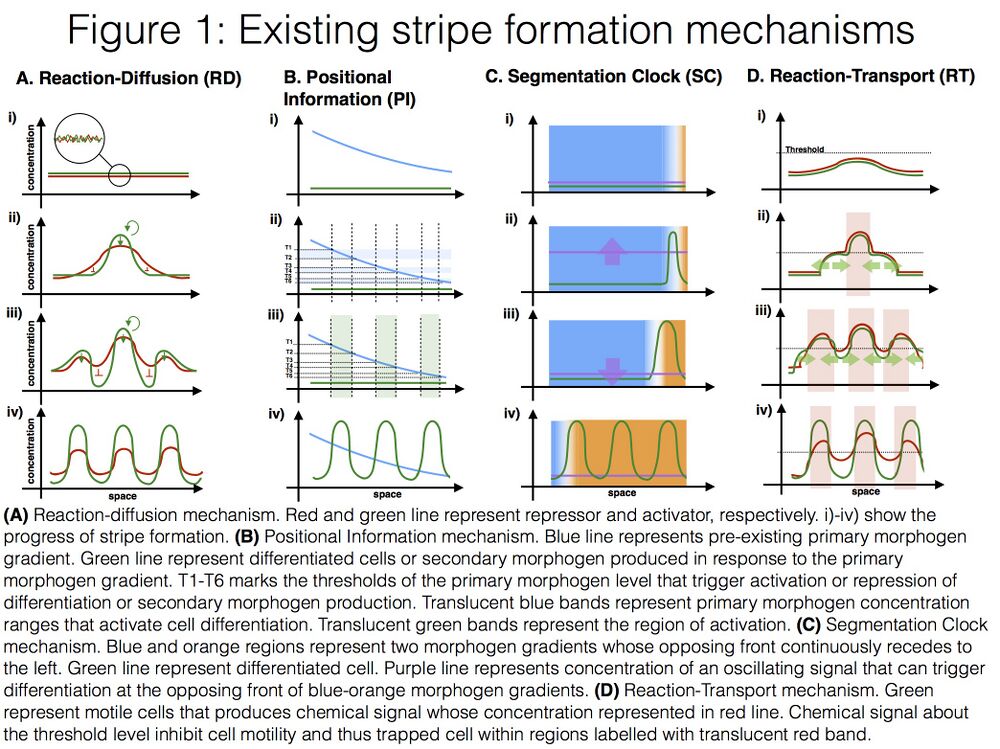
Early theoretical works in developmental biology feature the two archetypes of stripe forming mechanisms: Turing’s reaction diffusion (RD) model [Turing1952] and Wolpert’s positional information (PI) model [Wolpert1969]. RD generates patterns by amplifying local fluctuation of pattern forming agents (e.g. morphogens) (Fig 1A). Reaction kinetics as well as diffusion rate of morphogen determines which fluctuation modes will be amplified and, consequently, which shape and size of pattern will arise. PI generates patterns by having progenitor cells “read” their positions from a global morphogen gradient and differentiate accordingly (Fig 1B). Shape and size of an emerging pattern are determined by how the global morphogen gradient is prepositioned and how cells interpret their local morphogen levels. The same patterns could sometimes be explained by both RD and PI mechanisms [Green2015]. A notable example includes stripe formation in limb bud which determine the locations of digit and interdigit regions [Sheth2012; Miura2013]. It could be difficult or impossible to decide which mechanism is the true underlying process without looking into detailed gene regulatory networks and morphogen distributions. The main difference between RD and PI is that RD can by itself break a symmetry of an isotropic initial condition. On the contrary, PI needs anisotropic initial condition, i.e., pre-existing morphogen gradient that defines the direction and location on the pattern forming domain.
Another possible mechanism is to use segmentation clock (SC) to convert the temporal oscillation of a biochemical pacemaker into the periodic spatial pattern [Cooke1976] (Fig 1C). Similar to Wolpert’s original PI model, SC model needs an anisotropic initial condition, i.e., the presence of centralised pacemaker somewhere on pattern forming domain. However, SC generates repeating stripes sequentially using the same repeating process. This feature is more similar to RD model and not PI model which requires different stripes to respond to different morphogen levels. Yet, the other mechanism for generating stripes relies on reaction and transport (RT) of pattern forming agents [Liu2011] (Fig 1D). RT may be taken as a generalised RD. In Turing’s original RD model, pattern forming agents (e.g., morphogens) regulate one another’s production or degradation while their transport rate (e.g. diffusion coefficients) remain constant. In RT model, pattern forming agent may regulate one another’s production, degradation or transport rate. For instance, the first synthetic RT system by Liu et al has bacterial cell functions as a pattern forming agent whose transport rate (i.e. motility) is regulated by another pattern forming agent, AHL. Since individual cells produce AHL, the net AHL production at any location is positively regulated by cell concentration. Together, Liu et al system couples cell motility to cell density and consequently allows stripe pattern to emerge. Like Turing’s original RD system, RT system can break symmetry of isotropic initial condition and does not require centralised morphogen sources or pacemakers.
Reference/Resources
- Cooke, J, and EC Zeeman. "A clock and wavefront model for control of the number of repeated structures during animal morphogenesis." Journal of theoretica biology 58.2 (1976): 455-476.
- Green, Jeremy BA, and James Sharpe. "Positional information and reaction-diffusion: two big ideas in developmental biology combine." Development 142.7 (2015): 1203-1211.
- Liu, Chenli et al. "Sequential establishment of stripe patterns in an expanding cell population." Science 334.6053 (2011): 238-241.
- Miura, Takashi. "Turing and Wolpert Work Together During Limb Development." Science signaling 6.270 (2013): pe14-pe14.**commentary on Sheth2012
- Sheth, Rushikesh et al. "Hox genes regulate digit patterning by controlling the wavelength of a Turing-type mechanism." Science 338.6113 (2012): 1476-1480.
- Turing, Alan Mathison. "The chemical basis of morphogenesis." Philosophical Transactions of the Royal Society of London B: Biological Sciences 237.641 (1952): 37-72.
- Wolpert, Lewis. "Positional information and the spatial pattern of cellular differentiation." Journal of theoretical biology 25.1 (1969): 1-47.