Péclet number (Pe) - Nishanth Saldanha

Definition

The Péclet number (Pe) is a dimensionless number that represents the ratio of the convection rate over the diffusion rate in the a convection-diffusion transport system. ^[1][2]

[math]\displaystyle{ Pe = \frac{(Convection \, rate)}{(Diffusion \, rate)} = \frac {UL}{D} }[/math]

U represents linear flow in a control volume, L represents the length scale of the flow and D is the diffusion constant. This number can also be represented as a ratio of diffusive to convective time scales.

[math]\displaystyle{ Pe = \frac{(Diffusion \, timescale)}{(Convection \, timescale)} }[/math]

In diffusion dominated regimes, the Peclet number is less than 1. Such is the case with microfluidic systems, where turbulence is low. In convection dominated systems, this number is greater than one.

Derivation ^[3]

For a one dimensional system as described in Figure 1, with a specie concentration, [math]\displaystyle{ C }[/math] following relations can be made to relate flux in, [math]\displaystyle{ J_{in} }[/math] , flux out,[math]\displaystyle{ J_{out} }[/math] and control volume [math]\displaystyle{ V }[/math]. From this system, the Péclet number can be derived.

Figure 1 This is an illustration of a control volume with fluxes in and fluxes out. If sources and sinks can be neglected, these fluxes can be contributed to convection and diffusion

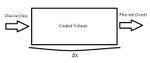
[math]\displaystyle{ V\frac{dC}{dt} = A\cdot J_{in} - A\cdot J_{out} }[/math]

This mass balance can be used to describe the flux into and out of the system. Flux is mass flow rate per unit area. Assuming inlet and outlet areas are constant, the mass balance can be simplified.

[math]\displaystyle{ \frac{dC}{dt} = \frac{A}{V}\cdot (J_{in} - J_{out}) }[/math]

If there are gradients in the system, the flux out of the system can be described as follows.

[math]\displaystyle{ J_{out} = \frac{\partial J}{\partial x}\cdot (\Delta x)+J_{in} }[/math]

Thus, the mass balance can be simplified as shown below.

[math]\displaystyle{ \frac{dC}{dt} = \frac{A}{V}\cdot \frac{\partial J}{\partial x}\cdot (\Delta x) }[/math]

Due to how the system is defined, [math]\displaystyle{ \frac{A}{V} = \frac{1}{\Delta x} }[/math]. Thus,

[math]\displaystyle{ \frac{dC}{dt} = \frac{\partial J}{\partial x}\rightarrow \frac{\partial C}{\partial t} =\triangledown J }[/math]

This equation is also described in three dimensions.

The assumption of negligible sources and sinks are made, so as to focus the system on diffusion and convection. Thus,

[math]\displaystyle{ J = J_{convection}+J_{diffusion} }[/math]

Mass flow rate, [math]\displaystyle{ Q }[/math], can be defined as [math]\displaystyle{ Q = C \Delta x\cdot A }[/math]. Since the convection is the prime source of this mass flow rate in this system, convective flux, [math]\displaystyle{ J_{convection} }[/math] is defined as such.

[math]\displaystyle{ J_{convection} = \frac{Q}{\Delta t\cdot A} = \frac{C \Delta x }{\Delta t} \rightarrow \frac{\partial x}{\partial t}C }[/math]

Diffusion equation can be derived from first Fick's law as shown below. [math]\displaystyle{ D }[/math] is the Diffusivity constant.

[math]\displaystyle{ J_{diffusion} = -D \frac{\partial C }{\partial x} }[/math]

Diffusive flux and Convective flux can be combined into the overall mass balance.

[math]\displaystyle{ \frac{\partial C}{\partial t} = -\frac{\partial \left [ J_{convection}+J_{diffusion} \right ]}{\partial x} = -\frac{\partial \left [ \frac{\partial x}{\partial t}C + -D \frac{\partial C }{\partial x} \right ]}{\partial x} }[/math]

Because the relation below can be applied, where [math]\displaystyle{ u }[/math] equals velocity of a particle, the mass balance can be simplified and described in multiple dimensions

[math]\displaystyle{ \frac{\partial x}{\partial t} = u }[/math]

[math]\displaystyle{ \frac{\partial C}{\partial t} = D\frac{\partial^{2} C}{\partial x^{2}} - u \frac{\partial C}{\partial x}\rightarrow \frac{\partial C}{\partial t} + u \frac{\partial C}{\partial x}= D\frac{\partial^{2} C}{\partial x^{2}} \rightarrow \frac{\partial C}{\partial t} + u \triangledown C= D \triangledown^{2} C }[/math]

Dimensionless numbers, as shown below can be used to restate the mass balance. [math]\displaystyle{ U }[/math] equals the convective linear flow rate.

[math]\displaystyle{ C^{*} = \frac {C}{C_{max}}; U^{*} = \frac{u}{U}; t^{*} = \frac {t}{t_{0}} }[/math]

When these numbers are applied, the balance is described as shown.

[math]\displaystyle{ \frac{C}{t_{0}}\frac{\partial C^{*}}{\partial t} + \frac{UC}{L}u^{*} \frac{\partial C}{\partial x}= \frac{DC}{L^{2}}\frac{\partial^{2} C}{\partial x^{2}} }[/math]

[math]\displaystyle{ \frac{L^{2}}{D\cdot t_{0}}\frac{\partial C^{*}}{\partial t} + \frac{UL}{D}u^{*} \frac{\partial C}{\partial x}= \frac{\partial^{2} C}{\partial x^{2}} }[/math]

The first term in the above balance is referred to as the unsteady term. In time invariant flows, this term equals zero. The ratio between the remaining two terms (i.e. the diffusive and convective terms), equals the Peclet number, as described below.

[math]\displaystyle{ Pe = \frac {UL}{D} }[/math]

References

[[1]] "Advection and diffusion of an instantaneous release". Heidi Nepf. 1.061 Transport Processes in the Environment. Fall 2008. Massachusetts Institute of Technology: MIT OpenCourseWare, License: Creative Commons BY-NC-SA.

[[2]] Incropera, F., DeWitt, D., Bergman, T., Lavine, A. Fundamentals of Heat and Mass Transfer”; Wiley: New York. 2011

[[3]] "Derivation of basic transport equation". Ali Ertürk. Lagoon Ecosystem Modelling (ECOPATH/ECOSIM): From Hydrodynamics to Fisheries. June 21- 23, 2011, University of Klaipeda and Leibniz Institute for Baltic Sea Research Warnemünde