Physics307L F09:People/sosa/Poisson
 Poisson Statistics Lab Poisson Statistics Lab
|
<html><img src="/images/9/94/Report.png" border="0" /></html> Notebook |
ObjectivesLab Partner: Manuel Franco In this lab we are going to detect random cosmic rays using the PMT and then we will see if those events fit the Poisson distribution. We will also learn how the Poisson distribution relates to the Normal and Binomial distributions. Equipment
Some images of the materials used Great pictures!
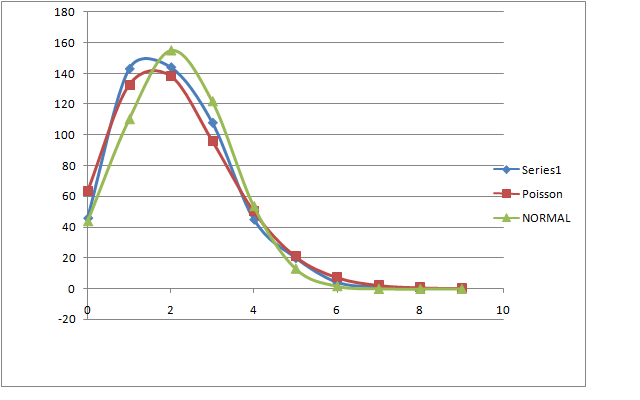
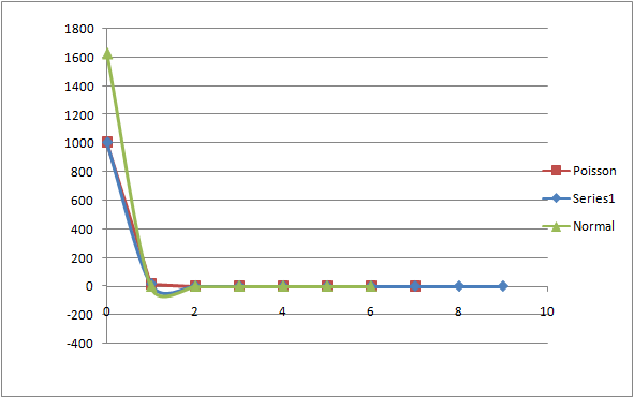
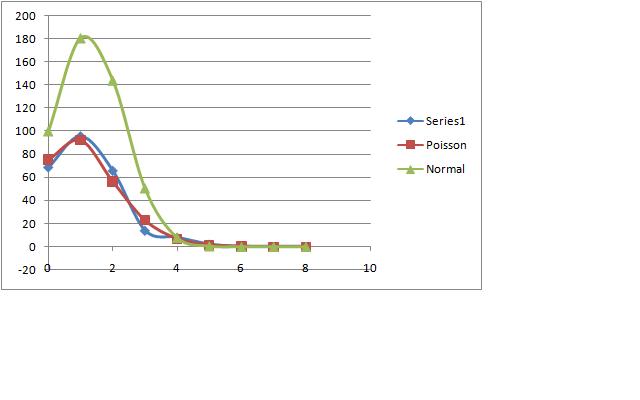
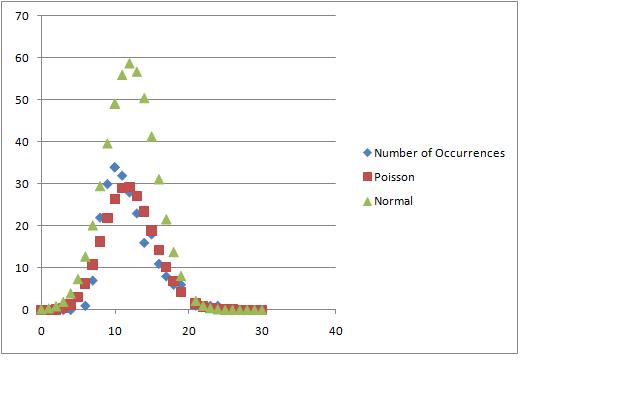
ProcedureFirst we familiarized ourselves with the instruments. We located the PMT and the scintillator which are one single unit. We then observed the high voltage power source and we set it up to 1000 V as suggested in the manual. We the proceed to manipulate the MCA to set it up in the MCS(Multichannel Scaling). We saw that the hydra cable was already ready. Then we started to manipulate the software and learn how to use. After mastering the use of the software we proceed to take many measurements. DataAll the colected data can be accesed in my notebook notes Data AnalysisThe excel spreadsheet used to analize the data can be found here. File:PoissonCalculations.xlsx 100 ms, 512 bins. 80 ms, 1024 bins. 800 ms, 256 bins. 1ms,256 bins.SJK 12:48, 11 November 2008 (EST)  You used the wrong normalization constant for the normal distribution on at least some of them. You use 512*NORMDIST() when 512 should be the number of channels. E.g., 256 channels in the final graph. When doing this, the fits are much better. ConclusionI don't really now if the graphs are correct since our we realized in the lab that the detection of cosmic rays was seriously flawed. However we can observe that some graphs do fit really well. I am not quite sure why this is, maybe just a coincidence. Anyway, even though our measurments were not the best, it does not prevent me for learning something. So here are some of the things I learned:
data fits a poisson distribution if the standard deviation of the data is equal or close to the standard deviation of the average. SJK 12:25, 11 November 2008 (EST) A lot of this is directly copied from wikipedia, and thus you need to put quotation marks and cite the source! I see that you cite the wikipedia article below, but that is not enough, since this is a direct quotation (copied exactly)...the way you formatted it, and since it was the majority of your conclusions, it looked like it was your own words.
Referenceshttp://en.wikipedia.org/wiki/Poisson_distribution Dr. Gold's manual. I based my analysis of the Poisson distribution on Annie's(from last year)analysis.
| |