Physics307L F09:People/Muehlmeyer/Balmer
Introduction
The gas tube is filled with a monoatomic gas, which has an electric discharge passing through it. This electric discharge excites the atoms of the gas through collisions with its electrons and the gas atoms are thus put into a higher energy state where their total energy is greater than it is in a normal atom. As it returns back to its normal state, it gives off that excess energy gained from the electric discharge and emits electromagnetic radiation. This electromagnetic radiation can be viewed using a prism, where we break up its spectrum into its component wavelengths.
Quantum mechanics tells us that the energy levels of these excited atoms are discrete, meaning that we will observe discrete wavelengths in the spectrum. Each substance has its own set of discrete wavelengths, a unique "signature" that is the basis of the art of spectroscopy.
In this case we will use Hyrdogren, which contains only one electron, and we will observe the part of its spectrum that falls within the range of visible light.
Balmer used the Hyrdogren spectrum to make an empirical formula that would represent the wavelengths of these spectral lines. The formula developed a relationship that was further developed by Ryderberg who found it easier to work with the reciprocal of the wavlengths. The Balmer formula became...
[math]\displaystyle{ \frac{1}{\lambda}=R(\frac{1}{2^{2}}-\frac{1}{n^{2}}) }[/math]
Where n=3 for the first line (largest wavelength), n=4 for the next line, etc. These numbers are now termed the principal quantum number, and represent the discrete energy levels above ground state.
Rydberg's constant today is considered to be: [math]\displaystyle{ R=1.0967758\cdot 10^{7} m^{-1} }[/math]
Which we will attempt to approximate in this lab.
We will do so by plotting [math]\displaystyle{ \frac{1}{\lambda} }[/math] VS. [math]\displaystyle{ \frac{1}{2^{2}}-\frac{1}{n^{2}} }[/math]
The slope of this line will give us Rydberg's constant. We will use the least squares method to find the slope.
Results
If you would like to see more details of my analysis please refer to my lab notebook:
or my excel data worksheet
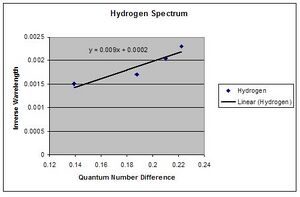
My Hydrogen Rydberg Constant:
[math]\displaystyle{ R=9.9(3)\cdot 10^{6} m^{-1} }[/math]
Which has a 9.37% difference to the actual value.
Comparison with Deuterium
We would like to know how our value for the Hydrogen Rydberg constant is different to the value of the Rydberg constant for Hydrogen's isotope Deuterium. We obtained data for Deuterium and proceeded with the same analysis...
My Deuterium Rydberg Constant:
[math]\displaystyle{ R=1.02(2)\cdot 10^{3} m^{-1} }[/math]
Deuterium (or "heavy hyrdrogen") is an isotope of Hydrogen. It contains a proton AND an nuetron, meaning that its nuclear mass is twice that of hydrogen.
The Balmer series equation for Hydrogen assumes the mass of the atomic nucleus to be infinitely large compared to the mass of its electron. However, in reality, this is not the case, and we must correct for the finite nuclear mass. This is done using the reduced mass, which takes the mass of the electron into account and creates a center of mass for the nucleus-electron system. SJK 19:19, 18 December 2008 (EST)

I'm not sure that's true that it's not corrected.
Deuterium's nuclear mass is doubled, meaning that yes, it will indeed have a different Rydberg value from Hydrogen, only because its spectrum is slightly different. We see that our Rydberg constant for deuterium is larger than the Rydberg constant for Hydrogen. You can see that this would be the case from the data. The spectral lines for Deuterium are shifted slightly to shorter wavelengths than that of Hydrogen.
Our comparison is in complete agreement with quantum mechanics and the correction for reduced mass.
Conclusion
We successfully obtained a ball park approximation to the Rydberg constant, and validated some quantum mechanical theory in our Deuterium comparison. I am slighly at odds with my linear least squares standard deviation. It outputted a large error value, which only allows me to display a Rydberg constant with one decimal place. Looking at our data, I do see that it had large deciations from my linear fit. There could have been some systematic error in our data taking, or in the equipment itself. Regardless, we did approximate the Rydberg constant to within 10%. I would say this is a descent success.