Physics307L F09:People/Mondragon/Notebook/070912
Mass of the Electron(first week)
Mass of the Electron(second week)
A procedure and introduction to this experiment can be found here
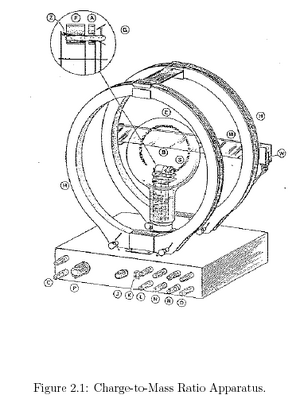
see comment

Excellent use of error estimates on your radii! A comment: you also should estimate the error on your "x" values (coil current or accelerating voltage)...this is important, too, for estimating the error in your final estimate.
Introduction
Electrons are boiled off a a cathode and are accelerated through an electron gun into a magnetic field at right angles to the velocity vector of the ejected electrons. The magnetic field is produced by two Helmholtz coils outside a nearly evacuated glass bulb that contains the electron gun and a tiny amount of helium gas. The magnetic field causes the electrons ejected from the electron gun to change their direction of travel, causing the electrons to travel in a circle until they hit the electron gun again. The electron travel path is observable if the apparatus is observed in a darkened room because as the electrons travel, some may excite the helium molecules in the bulb, resulting in a faint glow along the electrons' travel path. The radius of the circular travel path is strongly determined by the charge-to-mass ratio of an electron, the accelerating voltage of the electron gun (since this determines the initial velocity of the electrons once they enter the magnetic field), and the current fed into the Helmholtz coils (since this determines the strength of the magnetic field).
Objective
- Observe the motion of electrons in helium when in a magnetic field (B)
- Measure the radius of curvature of the electron ring with varying acceleration potential (V) and Helmoltz coil current (I)
- Determine the charge-to-mass ratio of the electron (e/m) from the path of an electron beam traveling in a magnetic fields of variable strength
- Expand our knowledge on electron motion in a B field.
Equations
A pair of Helmholtz coils produces a nearly uniform magnetic field. The field is perpendicular to the coils and has a magnitude given by the equation
[math]\displaystyle{ B=\left(\frac{4}{5}\right)^{3/2}\frac{\mu_0 N I}{a} }[/math]
in which [math]\displaystyle{ I }[/math] is the current running through the coils, [math]\displaystyle{ N }[/math] is the number of turns of wire in one of the coils, [math]\displaystyle{ \mu_0=4 \pi \times 10^{-7} \tfrac{N}{A^2} }[/math] is the permeability constant, and [math]\displaystyle{ a }[/math] is the radius of either coil. The apparatus we were using was configured so
[math]\displaystyle{ B=(7.8\times 10^{-4} \frac{\mbox{weber}}{\mbox{amp-meter}^2}) }[/math]
<img
style="width: 112px; height: 91px;" alt=""
src="http://ztec-inc.com/misc/form%202.PNG">
<img style="width: 120px; height: 73px;" alt=""
src="http://ztec-inc.com/misc/form%201.PNG">
<img style="width: 746px; height: 132px;" alt=""
src="http://ztec-inc.com/misc/form%204.PNG">
Procedure:
We started by setting up the test apperatus using
2 power
supplys and 1 multimeter. The supplys were used to supply the
test
apperatus with both the helmoltz coil current and the accelerating
potential. The multimeter actually measures the helmotz current (no
larger than 2A). After seeing the electron beam we started just playing
around with the settings just to get a feel for the setup and the test
apperatus. After we felt comfortable with the equipment, we started
taking measurements on the electron beam. The measurement procedure is
outlined in Professor Golds lab handbook. One thing that was not
documented was the use of the "focus" knob on the apperatus. We
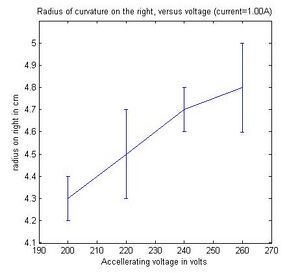
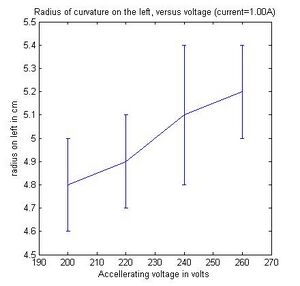
first first fixed the coil current to 1A, veried the accelerating
potential (V) from 200V, incremented the potential by 20V up to
260V measureing the radius of curvature at each incrument. We
determined the measurement error by observing the uniform width of the
beam from measurement to measurement. The same type of procedure was
done with data set #2 except this time we fixed the accelerating
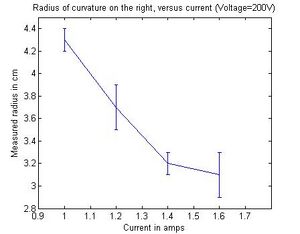
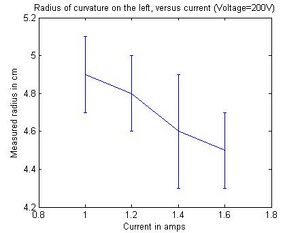
potential at 200V and varied the coil current starting from 1A to 1.6A
in .2A increments. In both data sets, before we measured the radius of
the beam, we adjusted the "focus" knob to "clean-up" the beam.
Observations:
In a magnetic field of strength B, the Lorenzts force acting on than electron with velocity v is F = ev x B. If the magnetic field is uniform, as it is in the Helmholtz arrangement, the electron follows a spiral (helix) path along the magnetic lines of force, which becomes a circle of radius r if v is perpendicular to B. As we increased the coil current we noticed that the ring was getting smaller (r was decreasing). By increasing the current the magnitic field became stronger and since the radius of of the electron path is proportional to the strength of the B field (from the equations above)and the e/m ratio decreases as well. The reason why we are able to see a visible light trail is because some of the electrons collide with helium atoms. The atoms are excited and ten radiate visible light. Furthermore, when we fixed the coil current and varied the accelerating voltage, the radius r increased significantly as did the e/m ratio which was translated a decrease in B field strength allowing the electron to be loosely bound. Something that we didn't now was that A unique feature of the e/m tube is that the socket rotates, allowing the electron beam to be oriented at any angle (from 0-90 degrees) with respect to the magnetic field produced by the Helmholtz coils.
Discussions:
-Using Lorentz equation to determine the work done by the electron -Determining whether or not we should include certain measurements in our running average estimation for radius of curvature -Why would might it be important to also include error measurements in accelerating voltage and coil current. What would be the advantages?
{http://ztec-inc.com/misc/Lab%202%20e_m%20calculation.xls RawData]
Fixed Acceleration Potential
(V) ***Note: The B
field had to be calulated to accomidate change in coil current. See Raw
Daa
| Accelerating Voltage (V) | Coil Current (A) | Radius Left (cm) | error | calculated E/M ratio | propagated error | Radius Right (cm) | error | calculated E/M ratio | propagated error |
|---|---|---|---|---|---|---|---|---|---|
| 200 | 1.00 | 4.9 | 0.2 | 2.7e11 | 2.2e10 | 4.3 | 0.1 | 3.6e11 | 1.7e10 |
| 200 | 1.20 | 4.8 | 0.2 | 2.0e11 | 1.7e10 | 3.7 | 0.2 | 3.3e11 | 3.6e10 |
| 200 | 1.40 | 4.6 | 0.3 | 1.6e11 | 2.1e10 | 3.2 | 0.1 | 3.3e11 | 2.0e10 |
| 200 | 1.60 | 4.5 | 0.3 | 1.3e11 | 1.7e10 | 3.1 | 0.2 | 2.7e11 | 3.4e10 |
| 200 | 1.00 | 4.8 | 0.2 | 2.9e11 | 2.4e10 | 4.3 | 0.2 | 3.6e11 | 3.3e10 |
| 220 | 1.00 | 4.9 | 0.1 | 3.0e11 | 1.2e10 | 4.5 | 0.1 | 3.6e11 | 1.6e10 |
| 240 | 1.00 | 5.1 | 0.2 | 3.0e11 | 2.4e10 | 4.7 | 0.2 | 3.6e11 | 3.0e10 |
| 260 | 1.00 | 5.2 | 0.3 | 3.2e11 | 3.6e10 | 4.8 | 0.1 | 3.7e11 | 1.5e10 |
=Summary
[math]\displaystyle{ Insert formula here }[/math]