Physics307L F09:People/Knockel/Notebook/071121
Electron diffraction
experimentalists: pinky and the brain
Goal
Electrons are waves that can diffract when going through crystals. Graphite is an allotrope of carbon where the carbon forms sheets of hexagonal patterns. The sheets of hexagonal carbon stack in a specific way that forms a crystal lattice that causes diffraction of electrons. I want to calculate certain dimensions of this lattice by measuring the diffraction of electrons through it when the electrons are aimed perpendicular to the sheets.
I have no clue what exactly I am measuring since 3D crystal latices form very complex diffraction patterns, but I know I am measuring some dimension of the crystal and calling it d. Maybe the physically significant measurement is 2*d or maybe 1/2*d, but this minor scaling can be done quickly (you won't have to redo the experiment and calculations...).
Equipment

- Cathode ray tube (CRT) that fires electrons through a few graphite sheets and has a fluorescent coated as a target. (Model TEL 2507)
- Multimeter for measuring current on the order of 0.25 mA = 250 [math]\displaystyle{ \mu }[/math]A
- Caliper for measuring diffraction rings
- The following power sources:
- high voltage up to 5 kV (for the accelerating voltage in the CRT)
- Up to 50 V (for something that makes everything work somehow)
- About 6.3 V AC (for the heating element in the CRT)
Setup
This is not important since figuring out a very specific technical device is not the purpose of the lab. Basically, we following a very elaborate circuit diagram from Dr. Gold to hook up the power supplies in a way that gives power to everything in the CRT. We also hooked up the multimeter so that it monitors the current to make sure that too many electrons are not sent through the graphite to destroy it (no more than 0.25 mA are allowed).
This took us a really long time. Even longer because the equipment we were initially given (power supplies and multimeters) were broken.
Procedure
Graphite is polycrystalline, which means that there are many subdivisions that each have a different orientation. These many subdivisions create circles of diffraction because each subdivision diffracts the light in a different direction. There happens to be 2 circles that are formed around the central beam (the central beam is made up of the electrons that went straight through the crystal without being diffracted).
All we are going to do is alter the voltage (V) that accelerates the electrons and measure the size of the circles (r). This [math]\displaystyle{ r }[/math] is the linear distance between where the central beam of electrons hits the screen and one of the circles, as measured by the caliper. This is not exactly the radius of the circle or any highly meaningful measurement because the fluorescent target is curved, but I will force it to be useful since it's the best measurement I can get. These measurements results can be used to find the slope of the line formed by graphing r(V-1/2), which can be used to find a dimension of graphite (d).
The weaker (about 50 V) power source would only complicate voltage measurements, so we kept it in the circuit but did not use it to create a voltage.
Seeing the rings was difficult, especially at a low accelerating voltage. This is most likely the source of almost all random error. We used a less dense spacing of voltages when the voltages were low since this data is not too great. We stopped increasing the voltage when the power supply could go no farther.
Nik had to take the data since I sucked at seeing the rings. The rings were fuzzy, so we took the measurement from the center of the fuzz (the brightest point).
Equations
As we all should but do not remember, the formula for the m=1 diffraction order is
[math]\displaystyle{ sin(\theta)d=\lambda\, }[/math],
where [math]\displaystyle{ \theta }[/math] is the angle of diffraction and [math]\displaystyle{ \lambda }[/math] is the wavelength of the diffracted particles. We eventually want to turn this into an equation containing only 3 variables: [math]\displaystyle{ d }[/math], [math]\displaystyle{ V }[/math], and [math]\displaystyle{ r }[/math].
[math]\displaystyle{ \lambda }[/math] in terms of [math]\displaystyle{ V }[/math]
The accelerated electrons convert all of their potential energy (PE=eV, where e is the charge of the electron) into kinetic energy (KE=p2/(2m), where m is the mass of the electron and p the momentum). Setting KE=PE and solving for [math]\displaystyle{ p }[/math] gives
[math]\displaystyle{ p=\sqrt{2meV} }[/math].
De Broglie's cute equation [math]\displaystyle{ \lambda }[/math]=[math]\displaystyle{ h }[/math]/[math]\displaystyle{ p }[/math] (h is Planck's constant) gives
[math]\displaystyle{ \lambda=\frac{h}{\sqrt{2meV}} }[/math].
The wavelength of the electrons depends on the accelerating voltage in the above way.
[math]\displaystyle{ sin(\theta) }[/math] in terms of [math]\displaystyle{ r }[/math]
I will make two approximations to do this:
- [math]\displaystyle{ sin(\theta)=tan(\theta) }[/math]
- The center of the fluorescent target is the point that is farthest away from the graphite on the opposite side of the CRT. I will assume that the distance (L) between the graphite and this point is the distance of a flat target instead of a curved target. I make this assumption so I can say that [math]\displaystyle{ tan(\theta)=r/L }[/math].
Both of these assumptions are reasonable for small [math]\displaystyle{ \theta }[/math].
As a result,
[math]\displaystyle{ sin(\theta)=\frac{r}{L} }[/math].
[math]\displaystyle{ r }[/math] as a function of 1/√[math]\displaystyle{ V }[/math]
Plugging in our [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ sin(\theta) }[/math] expressions into the topmost equation and solving for [math]\displaystyle{ r }[/math] gives
[math]\displaystyle{ r=slope\cdot\frac{1}{\sqrt{V}} }[/math],
where
[math]\displaystyle{ slope=\frac{Lh}{\sqrt{2me}\cdot d} }[/math].
Solving for [math]\displaystyle{ d }[/math] gives
[math]\displaystyle{ d=\frac{Lh}{\sqrt{2me}\cdot slope} }[/math].
Using these equations to find the slope from a linear fit and then [math]\displaystyle{ d }[/math] from the slope is not perfect because of the two approximations I made. The first approximation makes my [math]\displaystyle{ d }[/math] too small, and my second makes it too large (I know this because I also worked out much more exact formulas using chord lengths and other bullshit, but these formulas were WAY too messy for their slight benefit in accuracy). My second approximation makes [math]\displaystyle{ d }[/math] larger than the first approximation decreases it, so I should expect answers that are too large. I should also expect that, for the circle with larger [math]\displaystyle{ r }[/math] and therefor smaller [math]\displaystyle{ d }[/math], the systematic error should overshoot the actual value more than it overshoots the [math]\displaystyle{ d }[/math] for the smaller circle.
Values
The following are some fundamental constants needed to do the calculations:
- [math]\displaystyle{ h=6.626\times10^{-34} }[/math] J*s
- [math]\displaystyle{ m=9.1094\times10^{-31} }[/math] kg
- [math]\displaystyle{ e=1.6022\times10^{-19} }[/math] C
And the CRT length is
- [math]\displaystyle{ L=0.130(2)\, }[/math] m
Data
The "radii" were taken in inches up to three decimal places (eg 0.837 in), but I am converting these to meters (r1 is the smaller radius and r2 is the larger radius).
| V (V) | r1 (m) | r2 (m) |
|---|---|---|
| 2500 | 0.0167 | 0.0293 |
| 3000 | 0.0137 | 0.0262 |
| 3200 | 0.0135 | 0.0245 |
| 3400 | 0.0133 | 0.0229 |
| 3600 | 0.0127 | 0.0220 |
| 3800 | 0.0125 | 0.0212 |
| 4000 | 0.0121 | 0.0203 |
| 4200 | 0.0121 | 0.0208 |
| 4400 | 0.0110 | 0.0201 |
| 4600 | 0.0104 | 0.0198 |
| 4800 | 0.0103 | 0.0192 |
Calculations
In the following calculations, d1 corresponds to r1 and d2 to r2. MKS units are used to scale the figures. The error in the slopes is the standard error returned by Excel, and the error of the d's is the propagation of that error and the error in L. Also, although I significantly round the numbers I provide, I have not so in my calculations.
Finding d1
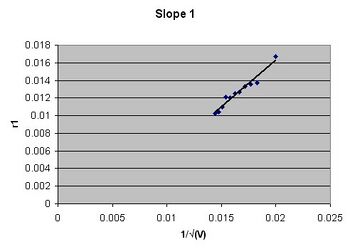
[math]\displaystyle{ slope1=1.06(7)\, }[/math] m*V1/2
[math]\displaystyle{ d1=0.151(11)\, }[/math] nm
Finding d2
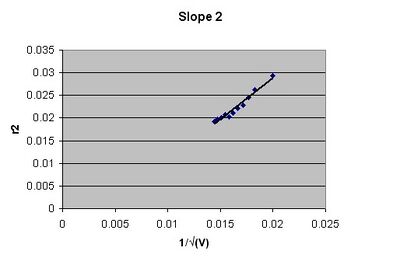
[math]\displaystyle{ slope1=1.82(12)\, }[/math] m*V1/2
[math]\displaystyle{ d2=0.088(6)\, }[/math] nm
Conclusions
The inner ring gives
[math]\displaystyle{ d1=0.151(11)\, }[/math] nm.
The outer ring gives
[math]\displaystyle{ d2=0.088(6)\, }[/math] nm.
The random error I have provided is due mainly to the fuzziness of the electron rings and Nik's imperfect (but still good) measuring abilities.
As for systematic error, this is due to approximations in deriving formulas, and it makes d1 slightly larger than it should be and d2 is affected more by this increase. This really shouldn't be a problem at all, but it's worth mentioning.
Another small source of error is that 5000 V gives the electrons a kinetic energy that is 1/100 of their rest energy, which means relativistic corrections would cause minor improvements.
I am pretty sure there is a large source of systematic error since I expected larger answers, and that it is probably the equipment. Because 1) standard multimeters cannot measure very high voltages and 2) the circuits in this experiment were stupidly overcomplicated, I am sure that the actual voltages that were accelerating the electrons were much less than those I used in my calculations, making the d values I have provided far too small. The more I think about it, the more I am sure of this. Especially because the equipment was acting goofy the whole time.
SJK 21:05, 1 December 2007 (CST)

A better diagram would be nice, but I'm not sure it's stupidly over-complicated. Not everything can be simple!
question
don't the electrons from the gun have to be in phase to diffract???
- Steve Koch 18:00, 1 December 2007 (CST):i.e. a coherent beam of electrons? Interesting question. If it were something where the absolute phase mattered in producing different diffraction patterns, then the differing phases of the incoherent electrons from the heated filament would smear out the pattern (I'm not sure what I mean by that). In this case, though, the pattern can be produced by a single electron wave interfering with itself. This has actually been demonstrated, one electron at a time. See: single electron double-slit experiment. So it's important that the wave function for a given electron remain coherent on all important paths (so for example, you can't "check" where the electron actually went without destroying the interference). To get a sensible answer, you should really talk with someone in the quantum info group :)