Physics307L F09:People/Ierides/The Balmer Series Formal Lab Report
The Balmer Series of Hydrogen and Deuterium in Atomic Physics
Author: Anastasia A. Ierides
Experimentalists: Anastasia A. Ierides, Alexandra S. Andrego
University of New Mexico, Department of Physics and Astronomy, Albuquerque NM, 87131
Physics 307L Junior Lab: December 14, 2009
aierides@nm.edu
Abstract
The importance of the Balmer series lies in the prediction of absorption/emission lines of hydrogen in the visible spectrum. The Balmer series led to the ensuing discoveries of the Lyman, Paschen, and Brackett series. These series predict the spectral lines of hydrogen in the non-visible parts of the spectrum. In order to detect the Balmer Series, of first Hydrogen and then Deuterium, we used a Constant-Deviation Spectrometer (which was calibrated using a Mercury Vapor bulb), in an environment with limited light, to measure the wavelength of the emission spectra of each. The excitation of the electrons in the atoms of each gas through electrical stimulation allows a release of photons at specific wavelengths corresponding to the Balmer series (the excitation of electrons from the first ionized state, [math]\displaystyle{ n = 2 }[/math], to the second, [math]\displaystyle{ n = 3 }[/math]). Then using a generalized form of the Balmer formula, the Rydberg formula, we used our measured wavelength to compute Rydberg's constant and to verify whether or not a deviation between the Hydrogen spectra and the Deuterium spectra could be found. Our calculated value of Rydberg's constant for each Hydrogen [math]\displaystyle{ (1.0972781 \pm 0.0025) \times10^7 }[/math] per meter and Deuterium [math]\displaystyle{ (1.0983221 \pm 0.0007) \times10^7 }[/math] per meter is in close proximity with the accepted value of [math]\displaystyle{ 1.0967758 \times10^7 }[/math] per meter.
Introduction
- The Balmer series a series of predicted and confirmed wavelengths of photons emitted from hydrogen spectrum belonging to the visible spectrum. It is the culmination of the excitation
of electrons from the n=2 state to the n=3,4,5, and 6 states in an atom causing a release of photons of corresponding energies [5].SJK 13:06, 15 December 2009 (EST)

Actually, the way you're describing it here and in your abstract is for absorption lines. Emission of photons is from the n=3,4,... states down to n=2
Also, your "background" section would need to be merged into this section for a typical formal report.
These wavelengths compose the visible part of the hydrogen spectrum and are hence called the Balmer series.

- The prediction of these spectral lines comes from the Balmer formula, written as:
- [math]\displaystyle{ \frac{1}{\lambda }=R(\frac{1}{2^2}-\frac{1}{n^2}) }[/math]
- [math]\displaystyle{ n=3,4,5,...\,\! }[/math]
- [math]\displaystyle{ \frac{1}{\lambda }=R(\frac{1}{2^2}-\frac{1}{n^2}) }[/math]
where [math]\displaystyle{ \lambda }[/math] is the wavelength to be predicted for each transition, [math]\displaystyle{ n }[/math] is the principle quantum number of the electron, and [math]\displaystyle{ R }[/math] is a constant called Rydberg's constant, derived as seen in the Appendix below [3]. This constant however is a variant one when it comes to dealing with various elements due to the reduced mass of the subatomic particles involvement in the calculation.
- The theory behind this constant and the above equation is that for every element, there is some value R for which the wavelength of each photon emitted by each transition can be
predicted. The discrepancy between the "R" values of hydrogen and deuterium is ever so slight due to the mass change of deuterium from its extra neutron, which in turn may or should cause a shift in the spectral lines [7]. To test this hypothesis, a "constant-deviation" spectrometer is used within an allowed precision to experimentally attain data to support this hypothesis [3].
- During our experiment we found that slight discrepancy in our values could be due to some oversight when using the 'scope'. There might have gear back lash from not turning the knob
all the way back before remeasuring spectra for each trial, even though we took great care in doing so. Also, the lab lasted over two days, with a week interval and during that interval another group had used the same device used for our experiment, so re-calibration for our set of data was necessary during the second day.
Background
- Before 1885, the year that the Balmer formula was founded by a Swiss school teacher Johann Jakob Balmer, physicists, although aware of atomic emissions, lacked the tools to
predict the location of each spectral line [5]. The Balmer equation is used in the prediction of each of the four visible emission/absorption lines of hydrogen with high precision. This had inspired the Rydberg equation, invented by a Swedish physicist Johannes Robert Rydberg [6]. This new equation was a generalization of the Balmer formula, which in turn "led to the finding of the Lyman, Paschen, and Brackett series used in predicting the absorption/emission lines of hydrogen found outside the visible spectrum" [5].
- According to the Rutherford Bohr model (devised by Neils Bohr in 1913 from the amelioration of a model created by Ernest Rutherford in 1911) of the Hydrogen atom, an electron
transition that occurs between the second energy level or first excited state in the atom (corresponding to n=2) and any other higher energy level results in the Balmer lines [8].
- The Balmer series has been helpful in astronomical and physical use for years due to the abundance of hydrogen in the universe. It has been used for several means such as
spectral classification, the measure radial velocities of objects in space due to doppler shifting, and the distances to those objects.
- The Balmer series is one of six series in which the spectral line emissions of hydrogen are designated. There are four different emission wavelengths of visible light by which the
hydrogen spectrum is defined. These wavelengths can be calculated using the Balmer formula (found by Johann Balmer, 1885) written above in the "Purpose" and reflect emissions of photons by transitions of electrons between principal quantum number levels from [math]\displaystyle{ n\geq3 }[/math] to [math]\displaystyle{ n = 2 \,\! }[/math] [5].
- Compared to the Hydrogen atom, which contains one proton in the nucleus, the Deuterium atom, contains a proton and a neutron in its nucleus. Thus the Deuterium atom is heavier
than the regular Hydrogen atom. By observing and classifying spectra lines of the hydrogen and deuterium atoms the Balmer series can be determined [7]. By using electrical stimulation to excite the atoms to higher energy levels we can measure the emitted photons of wavelengths equivalent to the energy of our excited electrons.
Materials and Methods
Apparatus: Constant-Deviation Spectrometer
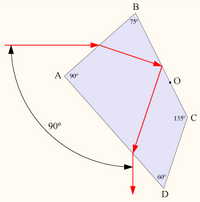
A constant-deviation spectrometer (SER. #12610) in use during this lab consists of a Pellin-Broca constant-deviation prism whose incident and exit angles are fixed with an appropriate rotation of the prism. The only requirement in this setting consists of keeping a the incident light ray and the axis of the analyzing telescope perpendicular [3].

Calibration of the Spectrometer


In order to calibrate our spectrometer we used a mercury vapor tube (S-68755-30-K). To start, the mercury tube was placed inside the spectrum tube power supply (Model SP200) and warmed for about five to ten minutes. Meanwhile, the spectrometer was adjusted such that the cross-hairs were brought into focus by adjusting the ocular to suit our vision. The slit was then brought into focus using the large ring near the center of the viewing telescope, turning the screw only in one direction to ensure that "gear backlash" can be avoided. This setup can be seen in Figure 3.
Using the spectrometer with a wide slit as seen in Figure 4, a line of the mercury spectrum could be distinguished and then, with a narrowed slit, the line was brought into focus until it was quite narrow and sharp.

Noting the orientation and value of the spectrometer dial, as seen in Figure 5, the corresponding wavelengths of light were applied as given in Table 1 [3]:
TABLE 1
Color Wavelength (nm) Deep Violet (very hard to see) 404.7 Violet 435.8 Very Weak Blue-Green skip this one Green 546.1 Yellow 1 577.0 Yellow 2 579.0 Red 690.75
The calibration of the spectrometer was then completed and the compilation of data was commenced.
Measurement of the Hydrogen and Deuterium Spectrum


After turning off the power supply and replacing the mercury spectrum tube with the hydrogen spectrum tube (S-68755-30-G), we allowed the hydrogen tube to warm up for approximately five minutes, as seen in Figure 6. Then we began to take measurements making sure not to dislodge the prism from its calibrated state. We began measuring the hydrogen spectrum by finding each spectral line, focusing it in the cross hairs, adjusting the slit width, and turning the dial to the appropriate wavelength as seen in Figure 7.
This process was repeated for a few more trials and then the bulb was replaced by the deuterium spectrum tube (S-68755-30-E) and the entire process used for the hydrogen spectral line measurements was repeated for the deuterium spectrum lines.
Results and Analysis
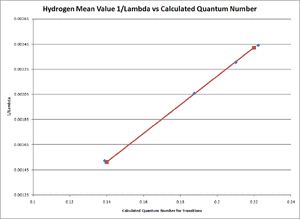
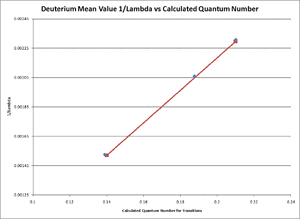
TABLE 2 is the accumulation of data taken during this experiment [12]. The transition column refers to the transition between quantum levels in an atom for electrons. The error margins were calculated using excel functions including the standard error and mean calculations.
The Balmer formula was used to compute Rydberg's constant for each hydrogen and deuterium as follows:
- [math]\displaystyle{ \frac{1}{\lambda }=R(\frac{1}{2^2}-\frac{1}{n^2}), n=3,4,5,6\,\! }[/math]
- [math]\displaystyle{ \frac{1}{\lambda }=R(\frac{n^2-4}{4n^2})\,\! }[/math]
- [math]\displaystyle{ R=\frac{4n^2}{\lambda(n^2-4)}\,\! }[/math]
- [math]\displaystyle{ \frac{1}{\lambda }=R(\frac{1}{2^2}-\frac{1}{n^2}), n=3,4,5,6\,\! }[/math]
The relationship between [math]\displaystyle{ \frac{1}{\lambda }\,\! }[/math] and the term [math]\displaystyle{ \frac{n^2-4}{4n^2}\,\! }[/math] for each hydrogen and deuterium separately were graphed linearly using excel as seen in Figure 8 and Figure 9. They resulted in a slope which was equal to the mean experimental value of the Rydberg Constant.
The mean measured experimental values for Rydberg's constant for each hydrogen and deuterium were calculate as:
- [math]\displaystyle{ R_{Hydrogen,average}\approx1.0973\pm 0.0025\times10^7 m^{-1}\,\! }[/math]
- [math]\displaystyle{ R_{Deuterium,average}\approx1.0983\pm 0.0007\times10^7 m^{-1}\,\! }[/math]
The accepted value for Rydberg's constant is given as [3]:
- [math]\displaystyle{ R_{accepted}=1.0973731568525\times10^7 m^{-1}\,\! }[/math]
Looking at our data, we came upon the realization that our measured experimental we discovered that our experimental Rydberg constant for either hydrogen or deuterium was a pretty good evaluation and computation of Rydberg's constant with a maximum difference of approximately [math]\displaystyle{ 0.001\times10^7 m^{-1} }[/math] from the accepted value, allowing for systematic and random error.
SJK 13:19, 15 December 2009 (EST)

It appears that you're comparing to the Rydberg constant for an infinitely massive nucleus. You should compare the results of H to a calculated value using reduced mass of electron and one proton, and compare D to calculation using one proton and one neutron.
Conclusions
In conclusion, in this lab we were able to measure the spectrum of each Hydrogen and Deuterium, each leading to the calculation of the Rydberg constant corresponding to each one. According to our data, although the Deuterium spectral lines varied from the Hydrogen lines in wavelength, as seen by the standard error measurement discrepancies in the Rydberg Constant of each, the variance is slight. The largest value by which the wavelengths varied was designated in the red wavelength measurement as seen in our data tables. This indicated some systematic error. Also according to our data, the wavelength measurements of each color seemed to be shifted from the Hydrogen in the Deuterium spectrum. The reason for this is the added mass in Deuterium due to the extra neutron compared to the reduced mass of just an electron and proton. In theory, no difference should be discernible with this kind of instrument. Possible reasons for these results are the two day split for data collecting, human error, systematic error, etc. Had the lab been kept in a controlled environment, one in which only the personnel working on a specific lab are allowed to adjust the instruments, perhaps systematic error could have been reduced. Overall, considering the values that were attained in a two-day period with an archaic instrument that was calibrated by other personnel between the two days of data collection, this lab could indeed be considered successful.
Acknowledgements
Please note that Alexandra S. Andrego was my lab partner for this lab. I thank her for her collaboration in the acquisition of data and helpful analysis.
Thanks to Professor Gold for using his lab manual [3] as a guide for the calibration process as well as a guide for data collection
Thanks to Antonio Rivera for the useful photos he had posted in his final lab report as well [11].
Also thanks to the many authors of Wikipedia for the useful open-access articles discussing the Balmer series [5], Rydberg's constant [6], and Deuterium [7].
Finally, I extend my gratitude to Professor Steven Koch as well as his teaching assistant, Pranav Rathi, for their extensive feedback as well as guidance throughout this lab.
References
SJK 13:10, 15 December 2009 (EST)

Kudos for very nice attribution to the sources that helped you out. You are, however, missing citations to original peer-reviewed research. (Wikipedia and hyperphysics use those original research reports to write their articles.)
[1] "Hydrogen energies and spectrum." Test Page for Apache Installation. N.p., n.d. Web. 13 Dec. 2009. http://hyperphysics.phy-astr.gsu.edu/Hbase/hyde.html#c4
[2] "Hydrogen spectrum." Test Page for Apache Installation. N.p., n.d. Web. 13 Dec. 2009. http://hyperphysics.phy-astr.gsu.edu/hbase/Tables/hydspec.html
[3] "The University of New Mexico Dept. of Physics and Astronomy." PHYSICS 307L: 'Junior Laboratory Manual Fall 2006'. Professor Michael Gold. http://www-hep.phys.unm.edu/~gold/phys307L/manual.pdf
[4] "User:Anastasia A. Ierides/Notebook/Physics 307L/2009/09/28 - OpenWetWare." Main Page - OpenWetWare. N.p., n.d. Web. 13 Dec. 2009. http://openwetware.org/wiki/User:Anastasia_A._Ierides/Notebook/Physics_307L/2009/09/28
[5] "Balmer series - Wikipedia, the free encyclopedia." Wikipedia, the free encyclopedia. N.p., n.d. Web. 14 Dec. 2009. http://en.wikipedia.org/wiki/Balmer_series
[6] "Rydberg constant - Wikipedia, the free encyclopedia." Wikipedia, the free encyclopedia. N.p., n.d. Web. 14 Dec. 2009. http://en.wikipedia.org/wiki/Rydberg_constant
[7] "Deuterium - Wikipedia, the free encyclopedia." Wikipedia, the free encyclopedia. N.p., n.d. Web. 14 Dec. 2009. http://en.wikipedia.org/wiki/Deuterium
[8] "Bohr model - Wikipedia, the free encyclopedia." Wikipedia, the free encyclopedia. N.p., n.d. Web. 14 Dec. 2009. http://en.wikipedia.org/wiki/Bohr_model
[9] "Balmer series." Department of Mathematics, Texas A&M University. N.p., n.d. Web. 14 Dec. 2009. http://www.math.tamu.edu/~comech/balmer/balmer.html
[10] "Pellin-Broca prism - Wikipedia, the free encyclopedia." Wikipedia, the free encyclopedia. N.p., n.d. Web. 14 Dec. 2009. http://en.wikipedia.org/wiki/Pellin-Broca_prism
[11] "Physics307L F07:People/Rivera/Notebook/Formal Report - OpenWetWare." Main Page - OpenWetWare. N.p., n.d. Web. 14 Dec. 2009. http://openwetware.org/wiki/Physics307L_F07:People/Rivera/Notebook/Formal_Report
[12] "Physics307L:People/Andrego/FormalReport - OpenWetWare." Main Page - OpenWetWare. N.p., n.d. Web. 14 Dec. 2009. http://openwetware.org/wiki/Physics307L:People/Andrego/FormalReport
Appendix
Derivation of the Rydberg Equation [5]
We can start from the equation of total energy of an electron in the nth energy state derived from the Bohr model:
- [math]\displaystyle{ E_\mathrm{total} = - \frac{m_e e^4}{8 \epsilon_0^2 h^2}. \frac{1}{n^2} \ }[/math]
The change in energy of an electron transitioning from one energy state with a value [math]\displaystyle{ n }[/math] to another is:
- [math]\displaystyle{ \Delta E = \frac{ m_e e^4}{8 \epsilon_0^2 h^2} \left( \frac{1}{n_\mathrm{initial}^2} - \frac{1}{n_\mathrm{final}^2} \right) \ }[/math]
Using [math]\displaystyle{ \frac{1}{ \lambda} = \frac {E}{hc} \rightarrow \Delta{E} = hc \Delta \frac{1}{\lambda}\,\! }[/math] to change the units to wavelength, we get
- [math]\displaystyle{ \Delta \left( \frac{1}{ \lambda}\right) = \frac{ m_e e^4}{8 \epsilon_0^2 h^3 c} \left( \frac{1}{n_\mathrm{initial}^2} - \frac{1}{n_\mathrm{final}^2} \right) \ }[/math]
where
- [math]\displaystyle{ h \ }[/math] is Planck's constant,
- [math]\displaystyle{ m_e \ }[/math] is the rest mass of the electron,
- [math]\displaystyle{ e \ }[/math] is the elementary charge,
- [math]\displaystyle{ c \ }[/math] is the speed of light in vacuum, and
- [math]\displaystyle{ \epsilon_0 \ }[/math] is the permittivity of free space.
And the Rydberg constant for Hydrogen is found as:
- [math]\displaystyle{ R_H=\frac{m_e e^4}{8 \epsilon_0^2 h^2}\,\! }[/math]
List of Used Constants
- [math]\displaystyle{ \mu\,\! }[/math] is the reduced mass of an atom
- [math]\displaystyle{ e=1.602\times10^{-19} C\,\! }[/math]
- [math]\displaystyle{ \epsilon_0=8.854\times10^{-12} F\cdot m^{-1}\,\! }[/math]
- [math]\displaystyle{ c=2.998\times10^8 m\cdot s^{-1}\,\! }[/math]
- [math]\displaystyle{ h=6.626\times10^{-34}J\cdot s\,\! }[/math]
- Rydberg's constant for hydrogen is calculated to be approximately:
- [math]\displaystyle{ R\simeq1.0967758\times10^7m^{-1}\,\! }[/math]