Physics307L F09:People/Gleicher/Formal
Measuring Planck's constant and an unknown work function via the photoelectric effect to discover relationship between the energy and frequency of light
Erron Gleicher
University of New Mexico Department of Physics and Astronomy
800 Yale Blvd. NE, MSC07 4220
Albuquerque, New Mexico 87131-0001
egleiche@unm.edu
Abstract
Planck's constant is a value that not only relates the frequency of light to its photon energy, but is also an important value in the field of quantum mechanics. I measured Planck's Constant and an unknown metal's work function using an apparatus that shined light of varying frequency on the metal and determined the maximum kinetic energy of the photo-ejected electrons for that frequency. After plotting frequency vs. kinetic energy, a least squares fit determined Planck's constant, h, and the work function of the metal. My measurements for Planck's constant using an average of the two orders is (7.24 +/- .02)E-34 J*s which gives me a 9.27% error from the accepted value for h of 6.626068 × 10-34 J*s.
The difference is outside my error bars implying that there was a systematic error in all of my measurements.
Introduction
Classically, electro-magnetic radiation was viewed as continuous waves of energy. The energy of the radiation is related to the intensity of the incident light and the intensity is proportional to the time-averaged square of the electric field. Accordingly, when a source of constant power illuminates an object for a period of time the imparted energy is dependent on the time of exposure.
Classical theory predicts that the amount of light emitted from a blackbody would increase as wavelength decreased but experiment showed that it decreased with wavelength. This is known as the "ultraviolet catastrophe" [1](under lab manual).
Background
The power output spectrum of a blackbody radiator was initially described by Wilhelm Wien in 1893 with the formulation of Wien's displacement law which stated that the maximum wavelength of emitted light would vary inversely with the temperature of the radiator (Wien, 1893):
[math]\displaystyle{ \lambda=\frac{b}{T} }[/math]
where b is Wien's displacement constant. This law was developed using thermodynamic techniques applied to EM radiation.
In 1905 a new theory was put forward by Lord Rayleigh (1842-1919) and Sir James Jeans (1877-1946). The "Rayleigh-Jeans law" states that the spectral radiance is inversely proportional to wavelength to the fourth power and proportional to the temperture (Jeans, 1905)(Rayleigh 1905).
[math]\displaystyle{ f(\lambda)=\frac{2*\pi*c*k*T}{\lambda^4} }[/math]
where c is the speed of light, k is Boltzman's constant, and T is temp in kelvins. While this described the spectral output at long wavelengths, it predicted that spectral output would tend toward infinity as wavelength approached zero. This was termed the "ultraviolet catastrophe".
Using a theory of quantized or "bundled" light energy, Max Planck (1858-1947) was initially able to reconcile the disagreement between theory and experiment regarding the emission from a blackbody radiator. In a paper originally submitted by Planck in December 1900, Planck proposed that the energy of a photon was related to the frequency by a factor of h, or Planck's constant:
[math]\displaystyle{ h*\nu=E }[/math],
Planck was awarded the Nobel Prize in 1918 for his theory of quantized EM radiation (or photon)(Planck, 1901). While initially relating the frequency of light to its energy, Planck's constant had a role in the development of quantum mechanics.
Albert Einstein (1879-1955) later used the photon concept to describe the photoelectric effect, wherein a photon impinging on a clean metal surface frees an electron from the metal. His theory stated that if a photon had more energy than the work function of a metal, then an ejected electron would be freed with a kinetic energy equal to the difference in energies.
[math]\displaystyle{ Etot=KE+\phi }[/math]
Einstein won the Nobel Prize in 1921 for his theory of the photoelectric effect. (Einstein,
In this report I attempt to compare my experimental results with the theories of quantized EM radiation and the classical vision of continuous radiation to determine which one is in better agreement with experiment. We will accomplish this using experimental equipment which utilizes the photoelectric effect to measure the kinetic energy of electrons ejected from a clean metal surface under the illumination of light of varying frequencies.
Materials and Methods
Materials
Using a mercury vapor lamp as a light source (Pasco Scientific, model no. OS-9286), the light is split by a transmission grating into its constituent lines. The different lines with varying frequencies can be focused onto our h/e apparatus (Pasco Scientific, model no. AP-9369) by varying the orientation of the grating/source with respect to the apparatus (Please see Fig 1.)
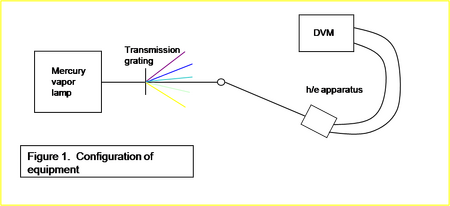
. The apparatus is described in the lab manual[2]. The outside of the apparatus has a white mask through which our light can be shone. The output of the apparatus is connected to a Keithley 131 Digital Multimeter by banana cables. The stopping voltage for the particular
frequency is directly read off by the multimeter.
Inside the apparatus is a metal with a variable applied reverse biasSJK 01:17, 7 December 2007 (CST)

ask me if this doesn't make sense...but remember how the reverse bias is actually applied by the electrons themselves?
. The apparatus has an op-amp circuit with very high impedance which allows the measurement of the voltage without draining the charging current.
If the energy of the impinging photons is greater than the work function than a current of photo-electrons is created. When a reverse biased voltage is applied, the current is reduced. If the voltage when the most energetic electrons are stopped is known, then the maximum kinetic energy of the electrons can be calculated.
Methods
To determine charging time vs. Intensity we timed how long it would take to reach a given stopping voltage for a given line while varying the amount of light that could get through a blocking filter. This was performed in the following manner:
1) The lines were sequentially focused on the apparatus mask, starting at one end of the spectrum. There were five lines in the resulting orders. They were in order of yellow, green, blue-green, blue, and blue-violet. Measuring the yellow and green lines required the use of spectral filters in front of the grating to prevent higher energy photons from hitting the apparatus.
2) The stopping voltage was determined for each line, and a stopwatch was used to measure how long it takes to reach approximately 90% of the maximum voltage.
3) Using the yellow and green lines, the intensity of the light was varied using a variable transmission filter to determine the effect of intensity on the energy transmitted. As the transmission was varied, the time to reach the 90% point was recorded.
The stopping voltage vs. frequency was measured by determining the voltage at which the photocurrent is completely stopped. This is determined by the h/m apparatus and read off using a DVM. We performed this measurement for all five lines, sequentially going from yellow to blue-violet. Two sets of data were taken.
The Determination of h involved measuring the stopping voltages of all five lines. Graphing the stopping voltage versus the frequency of the light will allow the extraction of the work function [math]\displaystyle{ \phi }[/math] and h from a least squares fit. Using several sets of data will increase the accuracy of the calculation.
Initially we were obtaining two very different values of h for the two orders we measured.
After considerable analysis a piece of lightly smoked Lexan© (polycarbonate) was used to block UV light from the green line in the second order. This considerably altered the stopping voltage and made it remarkably similar to the measured voltage for the green line in the first order.
Data Analysis
The data in this report was analyzed using Excel (Microsoft). The LINEST function was used to perform a linear regression of the data to determine the value of h and the work function Wo. The dependent variable is the energy while the independent variable is the frequency.
Results
The raw data can be found here: Physics307L_F09:People/Gleicher/Notebook/071008
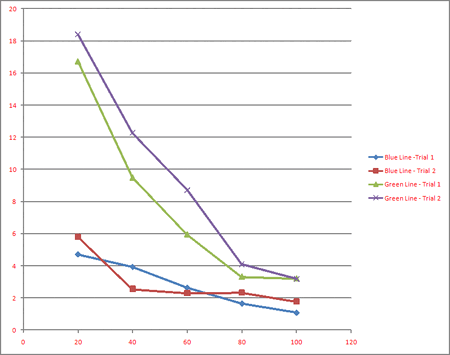
I: Charging time vs. light intensity
| Percentage | Trial 1 (s) | Trial 2 (s) |
|---|---|---|
| 100 | 1.09 | 1.78 |
| 80 | 1.66 | 2.34 |
| 60 | 2.65 | 2.30 |
| 40 | 3.94 | 2.56 |
| 20 | 4.72 | 5.81 |
Table 1: Charging time vs. intensity for the blue Line
| Percentage | Trial 1 (s) | Trial 2 (s) |
|---|---|---|
| 100 | 3.22 | 3.19 |
| 80 | 3.34 | 4.11 |
| 60 | 5.96 | 8.72 |
| 40 | 9.50 | 12.28 |
| 20 | 16.72 | 18.4 |
Table 2: Charging time vs. intensity for the green Line
SJK 23:23, 3 December 2007 (CST)

Good improvements. You have a typo in your formula (should be inversely proportional, and thus hyperbolic) You need to add labels to your graph axes. While you're at it...is there a way to plot the data so the data should be linear (change variables)?
The charging time vs transmission is shown in Figure 2 and Table 1 (color=) and Table 2 (color=). The percent transmission increases from left to right and charging time increases from bottom to top. It is apparent by the trends in the lines that increasing the transmission reduces the charging time. This can be explained by the photon theory in the following way: the photons all have the same energy but the filter reduces the amount of photons, which reduces the photocurrent, which causes the charging of the circuit to take longer.
[math]\displaystyle{ T \propto 1/I }[/math]
This data supports the theory, as shown in the previous equation.
Even though the rate at which the voltage accumulated was different for the varying transmissions, the final stopping voltages did not change.
II: Stopping voltage vs. frequency
SJK 23:59, 3 December 2007 (CST)

While you collected good data today, this section needs to be cleaned up. Too many things to list. For example, no table captions or numbers (should be numbered Table 3, 4, etc. since you have 1&2 above). One table seems to be repeated. The argument about photon theory of light is not very clear. Comparison with "accepted" value is not very strong...what is the percent error, and is the accepted value close to your range of uncertainty? If not, why do you suppose? What could still be going wrong? Some of this can go in your missing "conclusions" section.
For this section, the stopping voltages for five different lines were measured.
As the wavelength decreases the stopping voltage increases, hence the electron energy increases.
The results of my experiment support the quantum model of light. The intensity of the light did not have a real pronounced effect on the stopping voltage, whereas varying the wavelength of incident light significantly changed the stopping voltage.
At first my results for the first part of the experiment seem to support the classical theory such that the stopping voltage did vary with time, until it reached the point at which the current stopped. It is at that point that the stopping voltage becomes constant. This suggests that it indeeds takes time to reach the stopping voltage, but the final value does not increase with time. Whereas when the frequency of the impinging light is varied the stopping voltage is proportional to the frequency.
[math]\displaystyle{ KE \propto \nu }[/math]
Determination of h
By plotting several measurements from the first and second orders I hope to determine the value of Planck's constant, h, and the work function Wo.
This is the data that was taken:
First Order
| Line | Set 1 | Set 2 |
|---|---|---|
| Yellow | 0.725 | 0.726 |
| Green | 0.858 | 0.858 |
| Blue/Green | 1.510 | 1.501 |
| Blue | 1.717 | 1.698 |
| Blue/Violet | 2.112 | 2.075 |
Table 3: Stopping voltages for first order data.
Second Order
| Line | Set 1 | Set 2 |
|---|---|---|
| Yellow | 0.753 | 0.741 |
| Green | 0.849 | 0.866 |
| Blue/Green | 1.498 | 1.508 |
| Blue | 1.691 | 1.696 |
| Blue/Violet | 2.106 | 2.098 |
Table 4: Stopping voltages for second order data.
This is a link to my excel file with the calculations for Wo and h. File:Planck's constant(a).xls
(Steve Koch 23:28, 3 December 2007 (CST):Where is the link?)
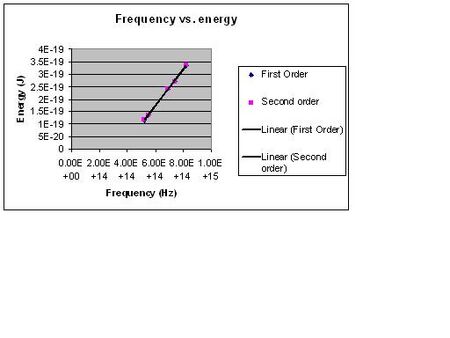
My values for the first and second order are as follows:
First Order
h = (7.23 +/- 0.1)E-34 J*s
Wo = (-2.59 +/- 0.06)E-19 J
Second Order
h = (7.15 +/- .16)E-34 J*s
Wo = (-2.54 +/- .10)E-19 J
Conclusions
My values for Planck's constant are (7.23 +/- 0.1)E-34 J*s and (7.15 +/- .16)E-34 J*s. The accepted value for Planck's Constant is 6.626E-34 J*s.
The value of the work function can be estimated by averaging the two values in the first and second order.
Wo = (-2.57 +/- .02)E-19 J.
Using the formula [math]\displaystyle{ % error= \frac{|a-b|}{b}*100 }[/math] where a is the measured value and b is the accepted value, I calculated a % error of 9.27%. The accepted value is not within my error bars.
I believe the reason for the discrepancy lies in the possibility that UV light slightly altered all the measured values for the stopping voltages. We used the Lexan© to block UV for only one line, but I believe if we had used the filter on all our measurements, we would have a value for h very close to the accepted value.
When repeating this experiment, the polycarbonate light shield should be used along with the recommended filters when measuring all of the lines.
SJK 01:21, 7 December 2007 (CST)

Your report just sort of ends abruptly here. I would move the work function result higher, and end with the discussion of most likely reason for discrepancy, followed by good idea for what to do next (if you were to do something)
References
Planck, Max. (1901). "On the Law of Distribution of Energy in the Normal Spectrum". Annalen der Physik, vol. 4, p. 553 ff.
Einstein, Albert (1905a), "On a Heuristic Viewpoint Concerning the Production and Transformation of Light", Annalen der Physik 17: 132–148.
Gold, M. (2006). PHYSICS 307L: Junior Laboratory. The University of New Mexico, Dept. of Physics and Astronomy. <http://www-hep.phys.unm.edu/~gold/phys307L/manual.pdf>
Jeans, J. H. Phil. Mag. 10, 91, 1905.
Rayleigh, J. W. S. Nature 72, 54, 1905.
Rayleigh, J. W. S. Nature 72, 243, 1905.
Rohlf, James William (1994), "Modern Physics from [math]\displaystyle{ \alpha }[/math] to [math]\displaystyle{ Z^0 }[/math]". Wiley and sons, First edition. p.65-75 & p. 77.
Wien, W. "Eine neue Beziehung der Strahlung schwarzer Körper zum zweiten Hauptsatz der Wärmetheorie". Verlag Harry Deutsch, Frankfurt am Main, 1893.SJK 00:51, 9 December 2007 (CST)

Do you know German? If so great. If not, make sure you only cite articles that you read (or read the important parts of)
Acknowledgements
I would like to thank the following people for their assistance in writing this paper: Mike Lancaster, Cary Dougherty, and Brian Ritter for helping to take data, and Dr. Koch for explaining the apparatus and motivating me to discover the source of systematic error that was effecting the values for Planck's constant.