Physics307L F09:People/Barron/Final rough
SJK 04:21, 8 December 2008 (EST)

This is a very good first draft. Many of the sections you have are very good, but there are a number of suggestions I have below. I particularly liked the ancient references you found related to data analysis and the speed of light...and I liked even more your style of putting brief descriptions of the references along with the citations. Very cool!
Speed of Light from a Cardboard Tube
SJK 03:31, 8 December 2008 (EST)

Your title made me laugh, so I suppose it suffices for capturing reader interest. Humorous titles are always risky...but this seems OK. Your contact info is good, but it would be difficult for a reader to contact you. You don't necessarily need to put your email address, but maybe a link to the department website, or the UNM directory if you don't want to put your email address.
Alexander T. J. Barron
Experiment conducted with Justin Muehlmeyer
Junior Lab, Department of Physics & Astronomy, University of New Mexico
November 17, 2008
Abstract
SJK 03:38, 8 December 2008 (EST)

I like your abstract--it is easy to read and very descriptive. It's a bit informal, which I think you should attempt to fix. For example, the phrase "which without correction nullifies any useful data taking ..." could be better said as "which must be minimized to prevent systematic error from dominating" or something like that. Also, you can strengthen the abstract by adding a motivating or impact statement to either beginning or end.
I measure the speed of light in air utilizing a time-to-amplitude converter (TAC), a photo-multiplier tube (PMT), and an LED pulse-generator in a light-tight environment. By positioning the pulse-generator at varying distances from the PMT/TAC apparatus, one can obtain various data sets corresponding to the change in distance between the two components. For each change in distance, the TAC manifests a new amplitude, corresponding to change in time readings. Plotting change in distance vs. change in time yields the perfect environment for taking a least-squares linear fit of the data, of which the slope is the speed of light in air. In the process of finding cair, I use different data-taking strategies as well as investigate a phenomenon known as "time walk," which without correction nullifies any useful data taking from this equipment set.
Introduction
SJK 04:13, 8 December 2008 (EST)

I was fascinated by the references you found and I was not aware of this kind of debate. I think you should expand a little bit on your discussion here to make it more clear. Since I was not familiar, I wasn't really sure what you were saying. Plus other things could clarified. For exmaple, what do you mean by "all experiments...involve takiing measurements of time take for light to traverse..." do you mean that all measurements are "time of flight?" Aren't the more precise methods indirect measurements: accurately measuring frequency and wavelength and thus deducing the speed? Even though you've found a couple fantastic references, it would be good to include a post-1944 reference related to our current modern-day accepted value of c.
Also, your introduction is very good as far as historical background. Next you should (1) mention where today's accepted value comes from and (2) briefly introduce your own experiment & lead into the rest of the paper.
Even after the Michelson-Morley experiment in 1887 gave reasonable doubt as the existence of the aether, certain scientists argued into the early 20th century against case for (what we now call) relativity, based on statistical uncertainty [1, 2]. Least-squares analysis specifically was targeted as covering up true values in its effort to smooth out errors, thereby burying results leading to aether-positive results. Through Einstein's theory of special relativity, and corroborating evidence, we now know almost irrevocably that the aether is not a factor in measurements of the speed of light, so good experiments involving least-squares analysis can be pursued with impunity.
All experiments measuring the speed of light involve taking measurements of time taken for light to traverse a given path[3]. The most common method up to 1944 was to partition light "packets" with periods of zero luminosity, thereby creating specific boundary times with which to measure between[3]. We follow this approach with more modern tools.
Methods and Materials
SJK 04:15, 8 December 2008 (EST)

You should make the methods past tense and "we did ___" kind of statements. Also, you should mention the manufactuer of equipment (when possible) and certain things that are missing (such as the oscilloscope, power supplies, etc.)
In order to measure the time-of-flight (TOF) of light packets, we position a moveable LED-pulse generator inside a several meter-long cardboard tube. The generator fills the entire cross-sectional area of the tube, ensuring light-tight conditions. On the opposite end of the tube, we position a fixed PMT. On the inner side of each device is a polarizer, used to maintain near-constant intensity of light received by the PMT. Constant intensity is needed to minimize the effects of "time-walk," addressed under Sources of Error below. The generator and PMT are both connected to the TAC, which measures the difference in time between the generation of the pulse and the receipt of the pulse by the PMT. The PMT is also connected to a digital oscilloscope through a second anode connection. We read the voltage output of the TAC via the oscilloscope along with the reading from the PMT.
With this setup, we can take data over a range of varying distance parameters, denoted in the following four trials. I denote change in distance as Δx:
i) large and increasing individual Δx over large total Δx,
ii) small, constant individual Δx over small total Δx,
iii) large, constant individual Δx over large total Δx, and
iv) medium Δx with no time walk correction.
For each Δx, we move the LED-pulse generator farther away from the PMT in intervals specified under Data below.
Sources of Error
Time walk is the principle source of systematic error in this experiment. It occurs due to the TAC's triggering off signals from the PMT via a fixed voltage threshold. If the signal from the PMT is small, the TAC will trigger later than it would for a larger signal. In order to combat this, we use rotatable polarizers in tandem to try and maintain constant intensity of light received by the PMT. The higher the intensity, the more photons interact with the PMT and a stronger signal results. The same is true in reverse.
We read the voltage amplitude from the TAC visually using cursors on the digital multimeter, so our measurements were not very accurate. We were aided by the averaging tool provided by the multimeter (Steve Koch: Didn't you use an oscilloscope, not a multimeter?) , which helped matters quite a bit.
Our device for measuring distance was a standard meterstick, whose accuracy compared to the standardized meter is not documented.
Data
SJK 03:46, 8 December 2008 (EST)

This note can be moved to the caption for the table. Also, this whole "data" section should be just incorporated in the results section.
NOTE: ALL ΔX VALUES MEASURED FROM THE ENDPOINT OF THE PREVIOUS MEASUREMENT
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| All voltages measured with ± .02 V measurement error. |
Results
Assume error to be standard error according to documented least-squares analysis[4], without taking error from the TAC voltage level into account.
SJK 03:41, 8 December 2008 (EST)

As I said in Justin's report, I like this method of presenting the results, even though I think it's not very common in publications. You and Justin differ in your plotting of the lower and upper bound best fit lines. I think the way he did it is correct (the intercept is correlated with the slope, so you adjust that to in order to make the lines go through the center of your data. I'm pretty sure that's the correct way to do it.
NOTE: AXES ARE SET TO "TIGHT," SO SOME DATA POINTS ARE ON GRAPH EDGES
| Trial | Graphic Representation | Trial | Graphic Representation |
|
Trial 1:
Upper Error Bound:
Lower Error Bound:
|
|
Trial 2:
Upper Error Bound:
Lower Error Bound:
|
|
|
Trial 3:
Upper Error Bound:
Lower Error Bound:
|
|
Trial 4: (no time walk correction)
Upper Error Bound:
Lower Error Bound:
|
|
SJK 03:45, 8 December 2008 (EST)

I like your graphs and tables. As I mentioned in Justin's report: make sure to number them and to refer to them by number in your text. Also, add descriptive captions to the entire table and / or the individual plots, so the reader can unerstand what is being presented without having to search through the rest of the paper.
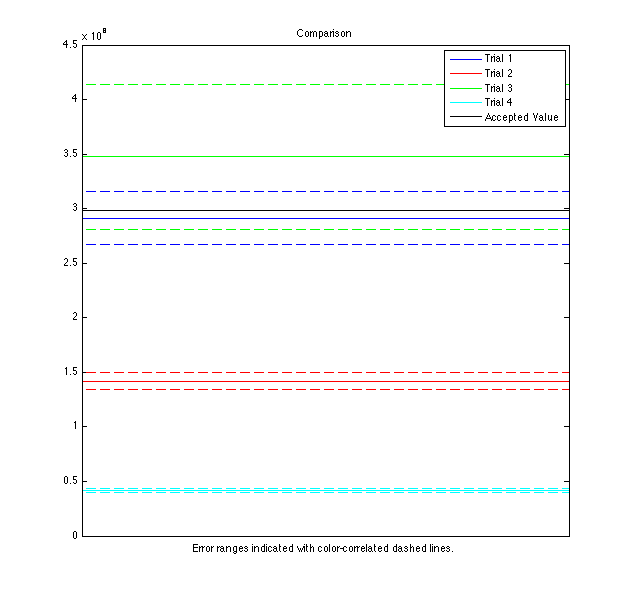
I notice that error range decreases with more measurements, but not necessarily accuracy. Here is a plot of all values with error compared to the accepted speed of light in air:
SJK 03:43, 8 December 2008 (EST)

I liked this graph when you first presented it with your informal summary. However, now I am thinking that it is a bit confusing. It would probably look better if all the data sets were not overlapping ... but if it were plotted instead with individual ranges next to each other (ask me if this doesn't make sense to you.
SJK 04:08, 8 December 2008 (EST)

the discussion is difficult to follow, and I suspect a large part of it is because of the informal nature of the discussion...more like how you would mull things over in your primary analysis notebook or your informal reports.
It appears that measurements taken over a large individual & total Δx, as in trials 1 & 3, yield the best results for c. Unfortunately, this experimental setup limits how much data can be taken this way, so the error is large. Small individual and total Δx in trial 2 yields an awful result, even though more data points narrowed the error range. The result of trial 4 illustrates how important adjusting for time walk is - c "walked" an entire order of magnitude! I wonder if taking data with small individual Δx over large total Δx would allow for the linear fit to filter out the "noise" from each small measurement in order to find the real trend of c. I believe the large amount of noise, from small x-stepping, combined with the small data range forced the trial 2 result far from its actual value.
This experiment and result illustrates the mechanics of accuracy of precision rather well. Trial 2 is not accurate at all, but is much more precise than our more accurate measurements. I believe the lesson to take away from this is that narrowing error isn't the entire battle - what good does small error do when the physical value isn't inside error bounds?
Upon comparison with the accepted value for the speed of light in air, this experiment seems fairly sound. Improvements in measurement of voltage amplitude from the TAC would be a relatively simple improvement to the process, and would increase the precision of the final result.SJK 04:05, 8 December 2008 (EST)

This would be a very good thing for you to attempt today!
Conclusion
SJK 04:07, 8 December 2008 (EST)

I am not really sure what you are saying in most of these conclusions, especially the last two sentences. As for the first sentence, why would you say it holds up fairly well? What is your criteria for assessing that?
This latest iteration of the classic time-of-flight measurement of the speed of light holds up fairly well to its predecessors[3]. Unfortunately, there is no discussion as to how many significant figures I can report truthfully in the final values. This process serves beginning experimentalists well in its simplicity and high potential for good results, as long as care is taken in the measurements.
Acknowledgements
Thanks to Miles Davis and Madonna, who really spiced up the data analysis. A big thank you to all the lab equipment- they're the real unsung heroes. Thanks finally to Justin, go team, Dr. Koch, go open science, and Aram, go physics!
References
SJK 03:58, 8 December 2008 (EST)

I really like the way you have done your references! The only time I can remember seeing comments in the references like you have done is in some review articles. Usually reference lists are very condensed lists of references, often without even the titles! Seeing what you have done here makes me realize that this should be a goal of publishing in this century, now that costs are not as strongly tied to number of pages or amount of text. It would just be so incredibly helpful if every the reference list as a rule included brief mention of which parts were used for the current paper.
Some more comments: (1) I still find it amazing that seemingly the most basic statistics were still being developed early last century and perhaps are even still under debate. Sometimes things seem so intuitive to me that I can't even understand what the debate is. In this context, Heyl's letter seems like hogwash to me now...It is interesting to imagine such a debate going on in those times. Or that you could write a letter like that and admit to not having really thought about the issue but nevertheless challenging entire fields of research. (2) Holy shit that is a thorough review on the speed of light measurements! I only have time to skim it right now, but very good find.
-
Heyl, Paul R. "The Application of the Method of Least Squares." Science, New Series, Vol. 33, No. 859 (Jun. 16, 1911), pp. 932-933. American Association for the Advancement of Science. JSTOR
Heyl argues that the method of least-squares to average out error may be flawed, specifically in the context of extended Michelson-Morley-like experiments. He proposes a "mathematical theorem," providing a rule of thumb regarding acceptable least-squares error analysis.
-
Freedman, Hugh D.;, Roger A.; Ford, and A. Lewis Young. Sears and Zemansky's University Physics: With Modern Physics. San Francisco: Benjamin-Cummings Pub Co, 2004.
-
Dorsey, N. Ernest. "The Velocity of Light." Transactions of the American Philosophical Society, New Series, Vol. 34, No. 1 (Oct., 1944), pp. 1-110. American Philosophical Society. JSTOR
Dorsey covers tomes of material in this paper, including a nicely-put summary of error analysis and the least-squares approach. He analyzes a number of historical experiments measuring the speed of light and reviews their accuracy based on procedure, equipment, and effectiveness of error documentation. There doesn't seem to be any mention of confidence intervals in a standardized way, but rather each uncertainty is reported based on logical arguments and various extremum.
-
Taylor, John R.. An Introduction to Error Analysis: The Study of Uncertainties in Physical Measurements. Sausalito, CA: University Science Books, 1996.