Physics307L F08:People/Osinski/Formal
SJK 04:28, 8 December 2008 (EST)

On the final version, you will need a descriptive title and author / contact information.
05:02, 8 December 2008 (EST): You have a lot of excellent material here, but some sections are completely missing. As you mention yourself, you do have some work remaining in terms of cutting out material and reorganizing things as I mention below. Please ask me for clarification in lab today.
Considerations for the Rough Draft
I made a number of changes to this report which I list below:
- got rid of unused data tables to emulate a more realistic publishable paper
- added units to tables and final results
- added linear fits to plots
- added a references section
- improved spelling
- corrected a misordering of labels in one of the tables
- used correct standard deviation of the mean formula for charge time errors
- redid error calculations from least squares fits for h and ω_0
- updated matlab code page
- although most real papers don't have lab notes like "we read the color wrong" I chose to leave most of these for now.
In general, more clean up needs to be done in the wording and excess information.
unfortunately I began editing the report on the original lab page so the original lab has been permanently modified. I realized this before I made any substantial subtractions to the report so that the original procedure along with the comments given by Prof. Koch are still available for comparison.
Since I had to work with the same data my values for h have not changed, but my errors have certainly become more reasonable. I intend to try to get rid of the systematic error that displaces our final result for h by attempting to measure the current leakage in the upcoming lab sessions. SJK 04:25, 8 December 2008 (EST)

This is a good idea for something to try tomorrow.
A Short Introduction to Planck's Postulate
SJK 04:34, 8 December 2008 (EST)

This introduction should be moved to after the abstract. Typically the section would be called "introduction," but you can use this title if you'd like. Your introduction reads very well. I would ordinarily argue for some mention and citation for how the modern accepted values of Planck's constant are obtained...I am not sure where you would insert that, though. Also, you will want to include specific citations to some refereed original research papers...and also make it more clear where you are obtaining this general historical info (e.g. is all of it from your textbook, or is it from a variety of sources?
It is arguably not an over exaggeration to say that Planck's constant is the most fundamental constant in quantum physics, because it arose from the earliest considerations of the quantization of energy. In response to the failure of the Rayleigh-Jeans formula to predict the finite energy density of a blackbody radiating at high frequencies (the ultraviolet catastrophe) physicist Max Planck decided to heuristically treat the energy as a function of frequency instead of representing it in terms of temperature. He could then treat the observed "hump" on the E density vs. fq graph as a version of the Boltzmann probability distribution. But Planck's great contribution came only when he realized that he could obtain the required cutoff (averageE → 0 as fq → ∞) if he modified the calculation leading from the probability distribution ((P(E)) to the average energy by treating the energy as if it were a discrete variable rather than a continuous one. With this insight he converted the integral of E*P(E) to a sum and found that the energy had to be directly proportional to the frequency. This proportionality factor would later bear his name with the minuscule value h=6.626068*10^-34 J-s.
Though Planck had been one of the first physicists to employ a discrete mathematics in describing radiation he was unsure whether or not energy was actually quantized or not. In a letter to R.W. Wood, Planck called his postulate "an act of desperation" (Quantum Physics, Eisberg & Resnick, pg. 21). It was not until later observations were made that the quantization of energy was thought to be a natural phenomenon and not just a clever mathematical interpretation. Among the most important of these observations was the fact that when light shined on a certain material electrons were emitted whose kinetic energies were independent of the light intensity and proportional to the light frequency. It was Albert Einstein, who was an early proponent of the reality of Planck's postulate even before Planck himself believed in it, who bravely made the step to arrive at a surprisingly simple linear formula (KE= hv + w) relating stopping potential to light frequency. The determination of the slope and y-intercept of this formula will be the aim of the following experimental procedure.
Abstract
SJK 04:30, 8 December 2008 (EST)

The abstract section should be directly after your title / contact information. The introduction should then follow the abstract.
You should include the uncertainty along with your value. Also, the abstract would be strengthened by some motivation sentence, probably at the beginning, which you can draw from your excellent introductory text.
We follow the procedure presented in Prof. Gould's manual to measure the charge time of the capacitor in an h/e measuring apparatus and the maximum stopping potential for various intensities and frequencies of light emitted by a mercury lamp incident on a photoelectric material. The light is separated into individual spectra with a prism, but effects of overlapping spectra are noted. A discussion on the imperfections of the measuring device is presented along with a thorough error analysis of the measurements. We find a linear relationship between frequency of light and voltage produced by the measuring apparatus which fits the formula [math]\displaystyle{ eV=h\nu-\omega_0 }[/math]. With a final result of 7.1876*10^-34Js we conclude that our experiment confirms the photoelectric effect.
Equipment and Setup
SJK 04:47, 8 December 2008 (EST)

even though they would be useful, bulleted lists of equipment are rare in formal publications (probably due to historical expense of printing). You should work these items into the procedure text. E.g., "All equipment from Pasco (CITYNAME) unless otherwise specified. We shined light from a mercury lamp (Model OS-9282) onto an h/e apparatus (AP-9368)...etc."
- Pasco OS-9282 Hg light source
- Pasco AP-9368 h/e Measuring Apparatus (Technical information is in the manual)
- Tektronix TDS 1002 digital oscilloscope
- Wavetek true RMS DMM
- Triangular Prism
A standard wall socket (120V) is used as power source for lamp and 2 9V batteries power the h/e apparatus.
Though we used the oscilloscope to to view the capacitor of the h/e Apparatus charging in real time it did not play an important role in the subsequent processes of measurement and data analysis.SJK 04:44, 8 December 2008 (EST)

if you don't end up using any oscilloscope data, then you do not need to mention it.
SJK 04:51, 8 December 2008 (EST)

From here and below, it appears that your methods are intermingled with your results and discussion. You will want to separate the methods parts (leave them up here in the methods section) from the results and discussion (make a new main heading for "results and discussion").
I. Measurement of Charge Time
SJK 04:49, 8 December 2008 (EST)

Much of this information would be helpful to a future experimenter...however, you're right in your thoughts above that you will want to delete much of the extraneous information to make it consistent with a formal report style.
In this phase of the procedure we measure the time it takes for the voltage reading of the h/e apparatus to reach a chosen value of cutoff voltage for two different frequencies of light, each of which is sent through a variable transmission filter with intensities of 20%, 40%, 60%, 80%, and 100%. We choose to make measurements using Yellow (5.18672E14Hz) and Violet (7.40858E14Hz) light incident upon the slit that opens up to the photoelectric material. It takes us three tries to get linear results and find an appropriate choice for stopping voltage for both colors. This difficulty in obtaining satisfactory results was mostly due to 1) an extra capacitance introduced by hand contact with the grounded h/e apparatus casing and 2) a failure to realign the light rays with the slit when the apparatus has moved. Cutoff voltages of 7V and 1.42V for yellow and violet light are finally chosen after realizing that the cutoff must be high enough so that a measurable charge time is required to reach it, but small enough so that it is not on the far tail of the charging scale where the voltmeter tends to jump back and forth between numbers as it slowly reaches the saturated stopping voltage.
In the following table cutoff voltage is measured in volts and time is measured in seconds.
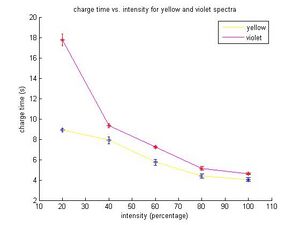
SJK 04:50, 8 December 2008 (EST)

Good caption on this figure. You will need to number your figures.
3RD TRY
Data 20% redo Color cutoff(V) time1 time2 time3 time4 time 5 Yellow 0.70 8.25 8.75 9.20 9.06 9.28 Violet 1.42 16.50 19.06 19.30 17.12 16.80 Data 40% redo Color cutoff(V) time1 time2 time3 time4 time 5 Yellow 0.70 8.00 8.42 6.72 8.75 7.59 Violet 1.42 8.72 9.68 9.68 9.75 8.84 Data 60% Color cutoff(V) time1 time2 time3 time4 time 5 Yellow 0.70 6.66 5.25 6.00 5.06 5.75 Violet 1.42 7.06 7.66 7.31 6.97 7.19 Data 80% Color cutoff(V) time1 time2 time3 time4 time 5 Yellow 0.70 4.37 5.19 4.13 4.25 4.03 Violet 1.42 4.41 5.44 5.22 5.25 5.46 Data 100% Color cutoff(V) time1 time2 time3 time4 time 5 Yellow 0.70 3.69 3.50 4.28 4.50 4.19 Violet 1.42 4.88 4.56 4.44 4.62 4.65
One of the experimentalists, Mr. Darrell Bonn, noticed that the time measurements tend to be longer when his hand is left touching the h/e apparatus after pressing the discharge button. We decide to redo the measurements of 40% and 20% for yellow and are finally satisfied with the apparent linearity of our measurements. We have noticed that, according to the Dr. Gould's manual, what we see as violet the manual terms “blue”.
II. First Measurement of Stopping Voltage vs. Frequency
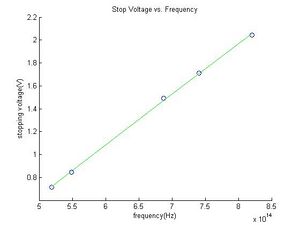
UV Violet Blue Green Yellow Max(V) 2.044 1.71 1.49 .847 with, .972 without .716 w/filter, .993/without
This behavior indicates to us that the frequency dependence of the stopping voltage is linear. Thus our experiment supports a quantum theory of light because a wave's energy is proportional to its intensity (and I recall that it is actually Intensity^2) but our measured voltages are not. If we assume that the quantum theory is correct then electrons are "knocked out" of atoms in the material because individual particle-like photons collide with them with an energy larger than their bonds. Then we would expect that even a single photon of sufficient frequency will impart enough energy on a bound electron to emit it with the same energy as a million photons would a million electrons. This expectation is confirmed by the observation that a lower intensity of light results in a lower emission current, which simply corresponds to lower number of emitted electrons, because the lower intensity light contains fewer particle-like photons.
III. Determination of h
We make measurements of stopping potential of the first and second order light bands according to the diagram on pg.38 of the procedure.
• First Order 1st run Color max(V) Ultra-Violet 2.030 As we turn the apparatus from UV to Violet we notice that V drops from Violet 1.515 2 to about 1.7 in between and then down to 1.5 on Violet. Past violet V Blue 1.707 rises again to 1.7. This is contrary to our expectations. Yellow 0.720 with filter, 1.335 without Green 1.234 with filter
We realize by closer inspection of the diagram in the procedure that we in fact were not measuring the first order light bands, so we redo the measurements at what we now believe to be the first order set of bands. This explains why the yellow line came before green and why “blue” had higher stopping voltage than “violet”.
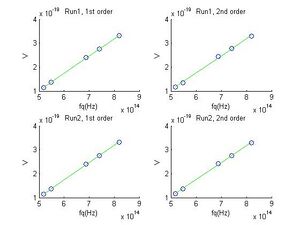
• First Order (redo) 1st run Color max(V) Ultra-Violet 2.064 Violet 1.718 Blue 1.493 Green .849 with filter, 1.007 without Yellow .717 with filter, 1.053 without Now we move to second order bands. • Second Order 1st run Color max(V) Ultra-Violet 2.062 Violet 1.731 Blue 1.520 Green 1.242 with filter, 1.335 without Yellow 0.735 with filter And the process is repeated. • First Order 2nd run Color max(V) Ultra-Violet 2.069 Violet 1.725 Blue 1.495 Green 0.850 with filter Yellow 0.714 with filter • Second Order 2nd run Color max(V) Ultra-Violet 2.061 Violet 1.725 Blue 1.515 Green 1.242 with filter Yellow 0.735 with filter
Effect of Overlapping Spectra
For some reason as of yet unknown to us the green band results in a much higher stopping potential in the 2nd order than in the 1st. We speak to Prof. Koch about this anomalous behavior and come to the conclusion that there must be an unseen factor at play. When we scan the h/e apparatus across the green band we notice that the voltage remains high even when we are in an apparent “dark” region on either side of green. When we cover the slit with both green and yellow filters we find that the stopping voltage of the green line is 0.842V! This result is very close to the measurement of the first order green line so we choose to use it instead of the out of place 1.242V. A second measurement of the second order green stopping voltage yields 0.849V. We have reason to believe that whatever unseen light made the voltage rise to 1.79V has been filtered out by this combination of filters (we also notice that the yellow filter does most of the filtering). After rereading the procedure it would be appropriate to add that the overlap of higher order UV spectra with lower order green is alluded to in section 5.3.1 of Prof. Gould's manual
Darrell has the idea that his reading glasses might work as a good UV filter rather than the yellow filter (since his glasses have clear lens UV filters). When he placed a lens over the slit we did in fact witness a stopping voltage of 0.847V for the second order green band.
Differences in Maximum Voltage as Intensity of Light Drops
With light shining upon the slit we measure the maximum voltage reached at consecutively higher intensities.
Blue Green 20% - 1.487V 0.846V 40% - 1.485V 0.850V 60% - 1.489V 0.852V 80% - 1.486V 0.852V 100% - 1.505V a noticeable difference 0.856V
We find a trend towards increasing voltage as intensity increases, but the quantum theory of light predicts that stopping voltage should only increase as a function of increasing frequency, not intensity. Rather than assuming that we have found evidence against the photoelectric effect, we believe the rise in voltage with intensity occurs because the photodiode exhibits an imperfection consisting of a current leakage. At lower intensities the total current in the apparatus is lower than at higher intensities so the leakage constitutes a larger fraction of the lower intensity current and is therefore more noticeable to the DVM. Thus the voltage reading from the unfiltered light most accurately reflects the actual kinetic energy of the emitted electrons because the current leak is small compared to the emission current.
IV. Data and Error Analysis
SJK 04:57, 8 December 2008 (EST)

Like I said above, your methods and results are currently mixed together. This section has quite a bit of good details about methods. Data analysis methods belong in the "methods" section (including mention of software and particular algorithms used for analysis). So, you should work on separating these methods from the results and discussion. As it is right now, the mixture of methods and results is really quite long and it is very hard for a reader to seek out the desired information. For example, readers often like to look at the results first and then gradually refer back to the parts of the methods that they care about. As it is written now, that is very difficult to do and thus the whole paper seems very daunting, despite your very good descriptions and data.
For convenience of viewing I have presented graphs next to their respective data sets above.
- Charge Time
We collected five data points at each intensity for both yellow and violet ("blue" in the manual, but it sure looks violet). I choose to represent the data by averaging the 5 times for each intensity and plotting both colors on the same axes with error bars. The MATLAB calling sequence for error bar plots is errorbar(X,Y,E) where E is a predetermined error. I choose to determine E by calculating the standard deviation of the mean for 'each' intensity so I will have to plot each point individually such that each of the 5 intensities will have its own error present (I could make just one plot with E set to the average std of the mean so that the error bars are all the same length, but what's 20 more minutes for extra accuracy?). After all this I calculate the mean of the standard deviations of the mean to provide an overall measure of error in the charge-time measurement. These procedures are undergone in the MATLAB code section entitled "Charge Time".
The standard deviation of the mean is calculated according to the formula
- [math]\displaystyle{ \sigma_m= \sqrt{\frac{1}{N*(N-1)} \sum_{i=1}^N (x_i - \overline{x})^2}\, }[/math]
After calculations and plots are completed I notice that the intensity vs. charge time plot for violet exhibits an unexpectedly high charge time at 20% intensity along with the largest error bar, so it is reasonable to ignore that point. The overall standard deviation of the mean including this stray point is
0.2423s
Without it the standard deviation of the mean reduces to
0.2036s
This is the value that I choose to present as the final result.
Our results show that as the intensity of light increases the time required to charge the capacitor in the h/e apparatus decreases, though this relationship does not appear to be linear as we previously thought it would. This actually makes sense because a capacitor does not charge linearly over time, but quickly at first and slowly at the end, following a negative exponential determined by the physical properties of the material and the magnitude of current coming its way. Our graph actually appears to be approximating a negative exponential of some kind. Though I cannot be sure at the moment what is the exact formula for this graph I can comment that it follows very nicely from the quantum theory of light. Were we to imagine millions of photons colliding with correspondingly millions of electrons in a material we would expect more electrons to be emitted when more photons are incident upon them (as long as the photon energy is large enough). More electrons correspond to higher current, which in turn correspond to lower charge time because the capacitor becomes saturated more quickly. A skeptic might ask why it is that the charge times for each intensity are shorter for higher energy (yellow) light than lower energy (violet) light when we would expect that emission current should only be proportional to intensity, not energy. I would respond that a higher energy light causes electrons to be emitted at higher velocities, so even though a cross-section of the yellow and violet light induced electron beams would have the same density of electrons at the same intensity, the electrons from the yellow light travel from the photoelectric material to the capacitor in a shorter time than do those emitted by the violet light. I could also comment on the skeptic's incredulity in expecting an undergraduate student to rigorously defend quantum physics.
- First Measurement of Stopping Voltage vs. Frequency
In the procedure we are asked to record the maximum stopping voltage reached during the charges and then comment on whether our findings support the wave or particle theories of light. Although we did follow this request it did not make much sense to us because we were only measuring the charge time for two frequencies. Instead of using limited data on which to base our conclusion we decided to make a separate set of measurements including each color at constant intensity. The results are plotted next to the corresponding data table above and the reasoning as to why they are in favor of the quantum theory of light is provided just below the table. Since these measurements were made for qualitative purposes only no error analysis is necessary here.
- Determination of h
We have four sets of data to analyze in this section: Two sets for the first order spectrum and two sets for the second. It should be noted that after considering the possible reasons for the existence of an unexpectedly high stopping voltage for the green band of the second order spectrum (discussed under the corresponding table above) we redid those measurements and obtained values of .842V for the first run and .849V for the second run. These values will be used in the ensuing analysis instead of those in the table. Once again, the graphs of the data are presented next to their corresponding table.
In the procedure we are asked to make plots, perform linear least square fits, and determine h and ω_o for each of the four data sets. I comply with these requests and use the frequency values provided in p.38 of Prof. Gould's manual to perform the necessary calculations which are present in the MATLAB code section entitled "Determination of h". Since our plots represent e*Voltage vs. frequency we can deduce from the equation
- [math]\displaystyle{ eV=h\nu-\omega_0 }[/math]
that the slope is h and the y-intercept is ω_o.
Procedure for Error Propagation
It is only recently that I received a copy of Taylor's informative text on error analysis. I have chosen to apply the methods of Chapter 8 (Least Squares Fitting) to my data and so I have redone this section of the error analysis completely. It will help me as well as the reader to explain the steps that will be taken.
1.) I begin by assuming a normal distribution to the stopping potential data following the relation y = A + Bx, which is going to be a very narrow distribution judging by the low deviation of the voltage data for each frequency. If we assume no substantial errors in the x variable the probability of obtaining the observed values of y (in my case eV) will be proportional to the Gaussian:
- [math]\displaystyle{ Prob_{A,B}(y_1,...,y_N) \propto \frac{1}{\sigma_y ^N} e^{-\chi^{2}/2} }[/math]
where [math]\displaystyle{ \chi^2 = \frac{\left(\sum_{i=1}^N (y_i - A - Bx_i)^2\right)}{\sigma_y ^2} }[/math]
and [math]\displaystyle{ y = eV }[/math], [math]\displaystyle{ A = -\omega_0 }[/math], [math]\displaystyle{ B = h }[/math] for this experiment.
2.) Since the best estimates for A and B are those values at which ProbAB(y1,...,yN) is maximum, or identically for which Χ^2 is a minimum, the least square fits for A and B (-ω_0 and h) are found by taking the derivative of X^2 with respect to A and B separately and then solving the resulting two equations for A and B. In the end
- [math]\displaystyle{ A = \frac{\sum_{i=1}^N x_i^2 \sum_{i=1}^N y_i - \sum_{i=1}^N x_i \sum_{i=1}^N x_iy_i}{\Delta} }[/math]
- [math]\displaystyle{ B = \frac{N\sum_{i=1}^N x_iy_i - \sum_{i=1}^N x_i \sum_{i=1}^N y_i}{\Delta} }[/math]
where [math]\displaystyle{ \Delta = N\sum_{i=1}^N x_i^2 - \left(\sum_{i=1}^N x_i\right)^2 }[/math]
I choose to perform this step using the MATLAB functions polyfit to find the coefficients (A & B) and polyval to evaluate them at at the data points for plotting.
3.) With the least squares coefficients determined I can proceed to calculating the errors of y (eV), A (-ω_0), and B (h). Taylor shows that the uncertainty for y (with x assumed to be without error) is
- [math]\displaystyle{ \sigma_y= \sqrt{\frac{1}{N-2} \sum_{i=1}^N (y_i - A-Bx_i)^2}\, }[/math]
I use this definition but divide by an extra N to make it the SDOM. This formula is generally similar to the familiar SDOM formula quoted above, except that it has a factor of N-2 in the denominator. This difference results from the fact that, in calculating uncertainty, we divide by the number of independent measured values. When we have to calculate the average of one quantity before the uncertainty we are left with N-1 independent measured values, ordegrees of freedom, but when we have to calculate the average of two quantities (A & B) then we are left with N-2 degrees of freedom. Taylor says that there are good statistical reasons to divide by the number of degrees of freedom instead of the number of measurements, but does not justify it mathematically. Qualitatively, though, this makes sense, for were we to measure just two pairs of data (x1,y1) and (x2,y2) with N=2 we could always get a straight line through two points so the idea of a linear fit for two points should be undefined, which is in this case a division by 0.
4.) With the uncertainty in y determined I finally calculate the uncertainties in the quantities that I am really interested in, A and B, or rather ω_0 and h. Taylor explains that from the two expressions for A and B above we can apply the general error propagation formula (summing partial derivatives times their respective uncertainties in quadrature) to arrive at the uncertainties for A and B (I repeat that I use the extra 1/N factor in my σ_y):
- [math]\displaystyle{ \sigma_A = \sigma_y\sqrt{\frac{\sum_{i=1}^N x_i^2}{\Delta}} }[/math]
- [math]\displaystyle{ \sigma_B = \sigma_y\sqrt{\frac{N}{\Delta}} }[/math]
where once more [math]\displaystyle{ \Delta = N\sum_{i=1}^N x_i^2 - \left(\sum_{i=1}^N x_i\right)^2 }[/math]
5.) In obtaining my final results I calculate the standard error of the mean (stdm) for each set of data, then average these errors for the total stdm of ω_0 and h.
Here are the results for the four data sets:
h1 = 7.1921e-034Js, stdm = 2.9322*10^-36Js || ω1 = 1.6097eV, stdm = 0.0123eV h2 = 7.1812e-034Js, stdm = 7.2352*10^-36Js || ω2 = 1.5954eV, stdm = 0.0304eV h3 = 7.2338e-034Js, stdm = 2.9684*10^-36Js || ω3 = 1.6246eV, stdm = 0.0125eV h4 = 7.1433e-034Js, stdm = 6.0527*10^-36Js || ω4 = 1.5807eV, srdm = 0.0254eV
The average h and omega are:
h = 7.1876*10^-34Js, stdm = 4.7971*10^-36Js
ω_o = 1.6026eV, stdm = 0.0202eV
Remarks on the Finals Results
SJK 04:58, 8 December 2008 (EST)

Note, Paul found a PASCO help page which stated the expected value of the work function (it was quite low but I don't remember the exact number...check for Paul's notebook.
The value for ω_o certainly indicates a material with a low work function (perhaps even too low when compared with values of standard materials which usually go only down to 2eV). Though my error is small I am not very happy with what it implies. Since my value is 5.6153*10^-34 units away from the accepted value of h=6.626068*10^-34 it would take many more than just two SDOMs to reach the accepted value from mine. In fact, the accepted value is about 11.7 SDOMs away from my value, so there is virtually no chance that I would obtain it with the measurement techniques I used. My hope of having a measurement with the accepted value within the 68% confidence interval (1 SDOM) is no where near being fulfilled. This overshoot is consistently reported in all four trials, so this implies that I have a good deal of systematic error in my measurements that has displaced all my data to average about a mean value higher than the accepted value. There are a number of reasons why I think this happened. These include accuracy with which we align the slit with the light rays, current leakage in the h/e apparatus, extra resistances influencing the measurements made by the DVM, and the possibility that the values of frequency given to us by the procedure which we used to make calculations were not the exact frequencies of the actual spectra shining upon our apparatus. My best guess is that the current leakage in the h/e apparatus actually resulted in the DVM getting a noticeably lower reading than it should for the lower frequency measurements because, as was stated before, the leakage constituted a larger percentage of the total current at these lower frequencies. This resulted in the left end of the V vs. fq to slump down, thus increasing the slope. I have not verified this in anyway, so it is only a guess. SJK 05:00, 8 December 2008 (EST)

The source of the systematic error will be a great thing to explore tomorrow. In your final version of the report, part of this section will become your "conclusions" and part of it will be in the "results and discussion" section.
References
SJK 04:27, 8 December 2008 (EST)

You will need some references to original peer-reviewed research in your final version. You can move me and Darrel to the acknowledgments section (which you will need to create)...anything in the references section should be specifically mentioned at least one time in the text of the paper or a figure caption.
- Quantum Physics, Eisberg & Resnick, pg. 21
- An Introduction to Error Analysis, John R. Taylor, Chapter 8
- Prof. Gould's manual
- Professor Steve Koch
- Darrell Bonn