Physics307L F08:People/Joseph/Notebook/071017
Poisson Statistics
Experimentalists: Nikolai Joseph and Bradley Knockel
SJK 00:51, 19 November 2007 (CST)

Great job on this lab! Sorry I didn't remember that you were finished. Because it's been so long, I'm not going to make a bunch of comments. A lot of the comments I made on Bradley's page would also be relevant for you: Bradley's page.
I liked your links to the hyperphysics stuff, that will be really useful. Reading through your report, I wasn't 100% sure that you were rock solid on where Poisson distribution comes from, that it converges to Gaussian, etc. With more careful writing, this would probably come across more easily. Same with discussion about your graphs, etc...it wasn't entirely clear what your conclusions were (Poisson is indeed necessary for low-counts). Very nice graphs, and I was impressed with your curiosity to take the long-time data.
Objective
By taking data that generates seemingly random data sets we hope to show that under certain circumstances the data fits a Poisson distribution. Also, a fair analysis of how the data is distributed in non-Poisson situations is in order. We are taking data that we believe to be of cosmic origin, over various apertures of time; for instance, 256 bins of 2 seconds each. The large amount of incidents being recorded over varying sized bins will give us a large variety of distributions.
Theory
When collecting large amounts of data it is wise to look at the probability distributions for that data. From the binomial distribution we can derive the Gaussian and Poisson distributions.
The Binomial Distribution
When analyzing any randomly distributed situation a binomial distribution:
[math]\displaystyle{ B(x)=\frac{N!}{x!(N-x)!}p^nq^{N-n} }[/math]
with a standard deviation of
[math]\displaystyle{ \sigma=\sqrt{pN(1-p)} }[/math]
and a mean of
[math]\displaystyle{ a=pN }[/math]
is used. With [math]\displaystyle{ N }[/math] = the number of counts, [math]\displaystyle{ p }[/math] = the probability of counts occurring, and [math]\displaystyle{ q }[/math] = the probability of counts not occurring. In all instances [math]\displaystyle{ p+q=1 }[/math], since something either happens or it doesn't, [math]\displaystyle{ p }[/math] and [math]\displaystyle{ q }[/math] must sum to 1. In context of our experiment, we have a very large [math]\displaystyle{ N }[/math] with a very small [math]\displaystyle{ p }[/math]. Undergoing several manipulations we can approximate the binomial distribution to be the Poisson distribution. More information can be found here
The Gaussian Distribution
When analyzing a situation in which there is a high probability of occurrence (large [math]\displaystyle{ p }[/math]) we use the Gaussian (or normal) distribution. The Gaussian distribution is given by
[math]\displaystyle{ G(x)=\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{\left(x-a\right)^2}{2\sigma^2}} }[/math],
with [math]\displaystyle{ a }[/math] = the mean, [math]\displaystyle{ \sigma }[/math] = the standard deviation. The Gaussian distribution is often used to model probabilities and is useful because if the standard deviation and mean are optimal then the actual mean and standard deviation values will match those given theoretically. A very good tool for understanding the Gaussian distribution can be found here
The Poisson Distribution
When analyzing a random situation in which there is a very low probability of occurrence (large [math]\displaystyle{ N }[/math] and small [math]\displaystyle{ p }[/math])we use the Poisson distribution. The standard form is given by:
[math]\displaystyle{ P(x)=e^{-a}\frac{a^x}{x!} }[/math]
with a standard deviation of
[math]\displaystyle{ \sigma=\sqrt{a} }[/math],
with [math]\displaystyle{ a }[/math] = the mean. The Poisson distribution appears only around zero and, unlike the Gaussian or binomial distributions, can only reflect positive integers. One can imagine a Gaussian distribution that has been normalized so it can only be positive values with a mean greater than zero (but not too much greater). A good tool for getting comfortable with Poisson distributions can be found here
Experiment
Setup and Equipment
We have a setup that consists of a photomultiplier tube that is attached to a NaI scintillator, both are housed in a structure of lead bricks. The arrangement is wired to a high voltage power supply (1000 volts) and then run through some sort of bridge and to a data acquisition board on a computer. The computer is running a program called PCAIII, which handles the data acquisition process. The photomultiplier tube and scintillator were connected by way of coaxial cables to the power supply which we connected to the bridge, and from the bridge into the computer. There were some erroneous cables coming from the data acquisition board that we had no need to mess with.
Procedure
Once we had all cables secured and the power supply and bridge were warmed up, we were able to start taking data. Using PCAIII we simply configured how many bins of data we were taking and how much time each bin would get ("dwell time"). We varied our bins from 256 (for 1s, 2s, and 10s) and 4096 (for 10ms, 100ms, and 100s). We experimented with the bins and determined the number of bins to be a 'resolution' of sorts. The more bins, the smoother the data became. We experimented and determined that we'd use a high number in some situations and a low number in others. It was mostly preference.
Data and Discussion
I couldn't figure out a good way to show uncertainty in the mean so I borrow from Bradley the idea of doing it thusly:
[math]\displaystyle{ a=a\pm SE }[/math]
where
[math]\displaystyle{ SE=standard\ error\ of\ the\ mean=\frac{\sigma}{\sqrt{number\ of\ bins}} }[/math]
We concluded that the uncertainty was not as much relevent to the data as it is to the process, and therefore should be considered. Since this data was gathered over several days, and from a completely uncontrollable source, there will be some fluctuation that is not necessarily error.
The data as follows.
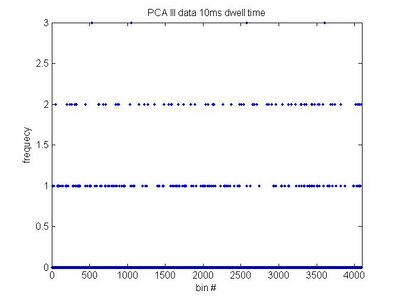
- 10 ms
- [math]\displaystyle{ a=0.07666\pm0.00527\, }[/math]
- [math]\displaystyle{ \sigma=0.3373\, }[/math]
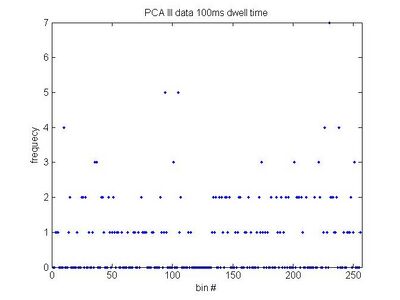
- 100 ms
- [math]\displaystyle{ a=0.6775\pm0.0157\, }[/math]
- [math]\displaystyle{ \sigma=1.006\, }[/math]
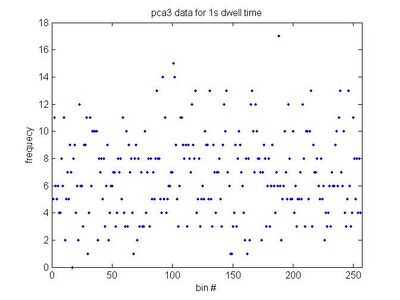
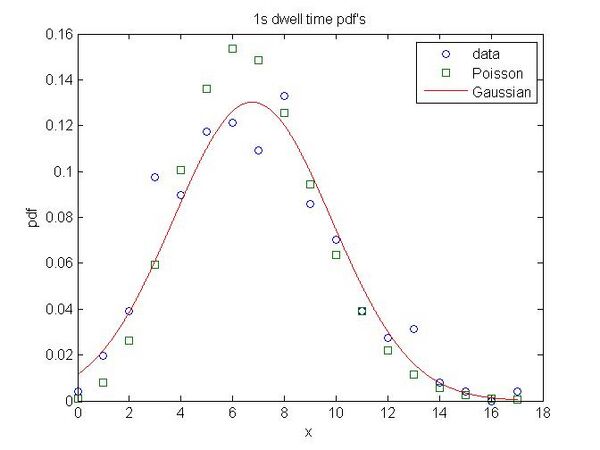
- 1 second
- [math]\displaystyle{ a=6.766\pm0.191\, }[/math]
- [math]\displaystyle{ \sigma=3.063\, }[/math]
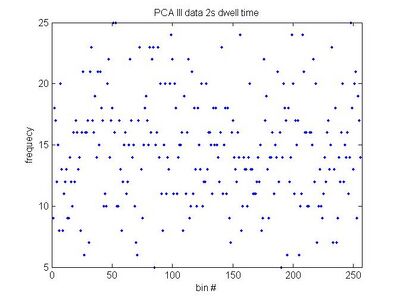
- 2 seconds
- [math]\displaystyle{ a=14.656\pm0.277\, }[/math]
- [math]\displaystyle{ \sigma=4.432\, }[/math]
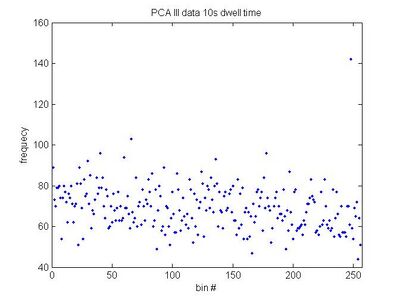
- 10 seconds
- [math]\displaystyle{ a=69.23\pm0.69\, }[/math]
- [math]\displaystyle{ \sigma=11.07\, }[/math]
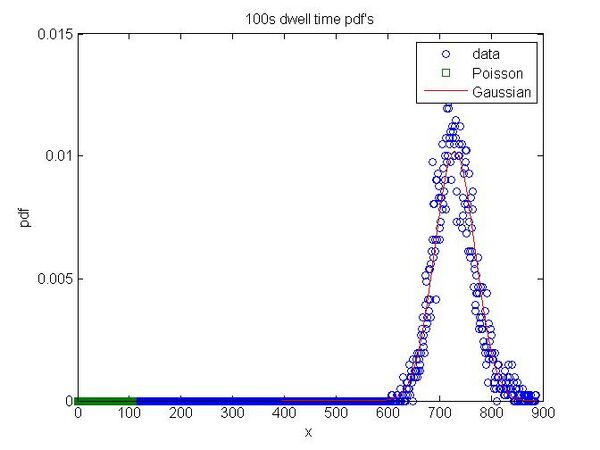
- 100 seconds
- [math]\displaystyle{ a=729.9\pm0.6\, }[/math]
- [math]\displaystyle{ \sigma=39.10\, }[/math]
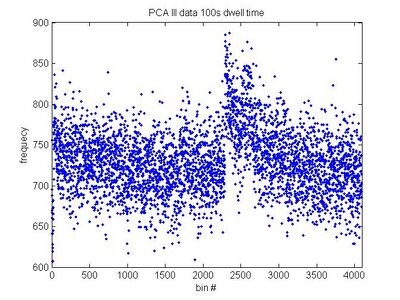
Notice the odd spike.
Error
This lab is really based on the notion of random error. The whole objective is to record events and to notice that they are distributed randomly. The source(s) of our data we presume to be of cosmic origin, but not of any specific origin that we can identify. We can't say, with any measure of confidence, what is exactly producing our data! Look at the graph for the 100 seconds data and notice the large, sharp spike. That is entirely inexplicable. Using our lead shielding and minimizing disturbances is really the best that can be done to control this experiment. With Bradley's help I was able to plot the Gaussian and Poisson distributions against our data and you can see that even though we have a good system for making predictions, the data does not always fit. On the longer time scales the data fits fine, but that isn't so much of what we are concerned about. Beside each distribution I give the error from the data in terms of either Gaussian or Poisson.
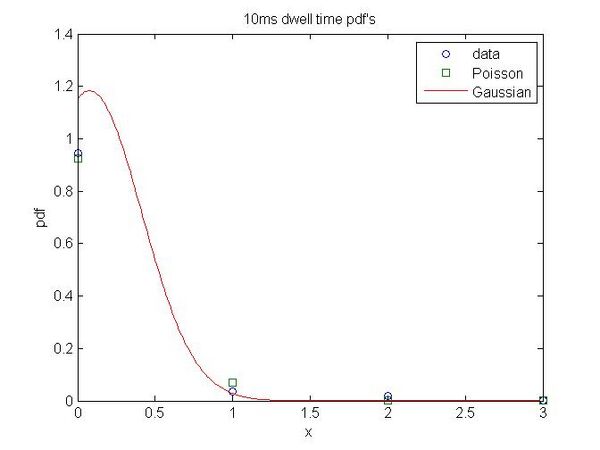
- 10 ms
- [math]\displaystyle{ Error_{Poisson}=0.0172 }[/math]
- [math]\displaystyle{ Error_{Gaussian}=0.0592 }[/math]
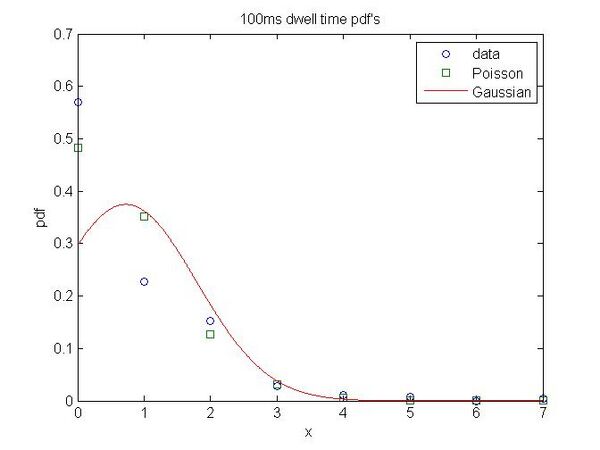
- 100 ms
- [math]\displaystyle{ Error_{Poisson}=0.0321 }[/math]
- [math]\displaystyle{ Error_{Gaussian}=0.0589 }[/math]
- 1 second
- [math]\displaystyle{ Error_{Poisson}=0.0123 }[/math]
- [math]\displaystyle{ Error_{Gaussian}=0.0082 }[/math]
- 2 second
- [math]\displaystyle{ Error_{Poisson}=0.0097 }[/math]
- [math]\displaystyle{ Error_{Gaussian}=0.007 }[/math]
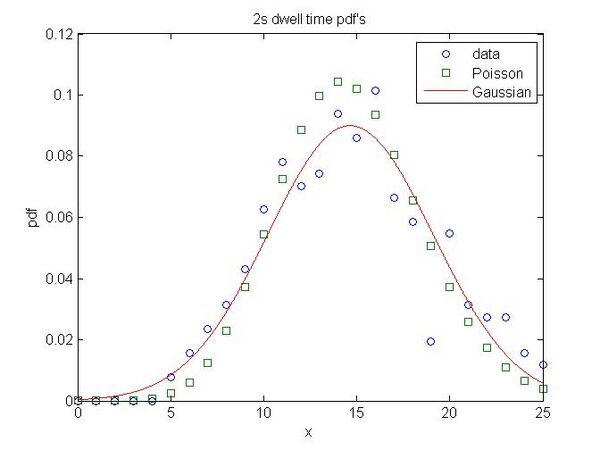
- 10 second
- [math]\displaystyle{ Error_{Poisson}=0.0032 }[/math]
- [math]\displaystyle{ Error_{Gaussian}=0.0028 }[/math]
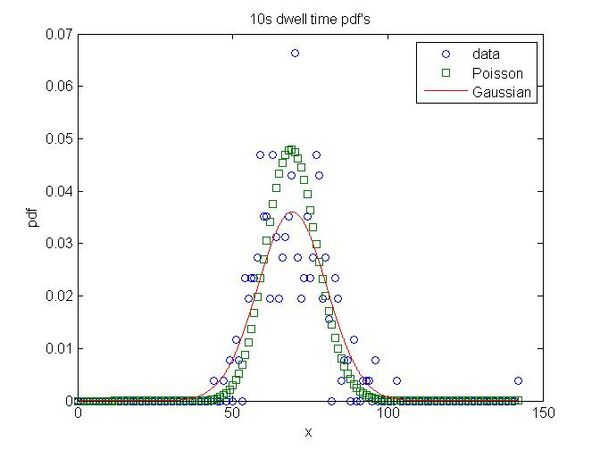
- 100 second
- [math]\displaystyle{ Error_{Poisson}=not real number! }[/math]
- [math]\displaystyle{ Error_{Gaussian}=0.002 }[/math]
Notice how quickly the Gaussian error drops off after 100 ms and also notice how the Poisson error is highest on the most Poisson looking distribution!
Conclusions
In situations where a Poisson distribution fits the data well, look for a low standard deviation. As the number of successful trials climbs, the Poisson won't be as useful and the Gaussian takes over. Unless it is your goal and you have a question to answer with it, avoid taking data from space.