Physics307L F08:People/Barron/Final final
SJK 17:30, 16 December 2008 (EST)
Excellent final report, Der!
Speed of Light from a Cardboard Tube
Alexander T. J. Barron
Experiment conducted with Justin Muehlmeyer
Junior Lab, Department of Physics & Astronomy, University of New Mexico
December 14, 2008
Abstract
I measure the speed of light in air utilizing a time-to-amplitude converter (TAC), a photo-multiplier tube (PMT), and an LED pulse-generator in a light-tight environment. By positioning the pulse-generator at varying distances from the PMT/TAC apparatus, one can obtain various data sets corresponding to the change in distance (Δx) between the two components. For each Δx, the TAC manifests a new amplitude, corresponding to change in time (Δt) readings. Plotting Δx vs. Δt yields the perfect environment for taking a least-squares linear fit of the data, of which the slope is the speed of light in air. In the process of finding the speed of light in air, I investigate the comparative effectiveness of varying rates of change in Δx. I also investigate a phenomenon known as "time walk," which introduces systematic error significant enough to render the experiment unreliable. I address and minimize this phenomenon to obtain experimental values statistically comparable to the accepted value of the speed of light in air.
Introduction
SJK 17:19, 16 December 2008 (EST)
Even after the Michelson-Morley experiment in 1887 gave reasonable doubt as the existence of the aether, certain scientists argued into the early 20th century against the case for (what we now call) relativity, based on statistical uncertainty [1, 2]. Least-squares analysis specifically was targeted as covering up true values in its effort to smooth out errors, thereby burying results leading to aether-positive results. Through Einstein's theory of special relativity, and corroborating evidence[3][4], we now know almost irrevocably that the aether is not a factor in measurements of the speed of light, so good experiments involving least-squares analysis can be pursued with impunity.
All experiments measuring the speed of light prior to 1944 involved taking measurements of time taken for light to traverse a given path[5]. The most common method up to 1944 was to partition light "packets" with periods of zero luminosity, thereby creating specific boundary times with which to measure between[5]. Such methods are labeled "time of flight" experiments. Since then, more sophisticated experiments successfully corroborated and improved upon the accuracy of older values. Lasers were at the forefront of the new experiments, which used observations of frequency to more clearly define the speed of light[6][7].
The contemporary accepted value of the speed of light is 299,792,458 m/s[8], as is defined by the specified measure of a meter, combined with the standardized measurement of a second by the Bureau International des Poids et Mesures(BIPM). This value reduces to 2.997 E 08 m/s in air at STP.
Recently, experimentalists have performed experiments aiming to challenge the canonical speed of light, trying to bend the seemingly impenetrable causality barrier resulting from the velocity maximum currently understood. The two extremes of such experiments consist of either slowing the speed of light down to an infinitesimal fraction of its normal magnitude through various creative physical media, or speeding up the group velocity of light pulses to find a speed greater than the standard[9]. Such experiments do not threaten the accepted theory of special relativity and causality, however, as no physical laws are broken via such means[10].
Even in view of all the advances in experimental methods to determine the speed of light, careful data-taking in well-designed time-of-flight experiments can yield results statistically very close to the standardized value. I accomplish this via a simple experimental setup, outlined below, and a statistical least-squares analysis.
Methods and Materials
SJK 17:23, 16 December 2008 (EST)
Your diagram kicks ass! It really makes the methods so easy to understand, very well done.
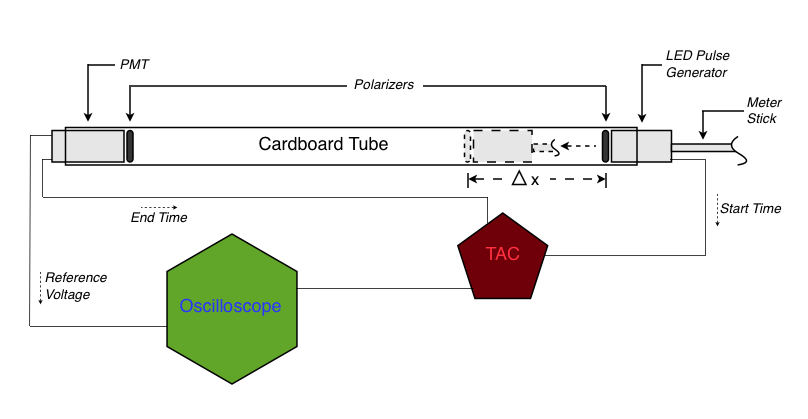
In order to measure the time-of-flight (TOF) of light packets, we positioned a moveable LED-pulse generator (custom) inside a several meter-long cardboard tube. The generator filled the entire cross-sectional area of the tube. On the opposite end of the tube, we positioned a fixed PMT (Perfection Mica Company, #N-134), which also filled the cross-section, ensuring light-tight conditions. On the inner side of each device was a polarizer, used to maintain near-constant intensity of light received by the PMT. Constant intensity was needed to minimize the effects of "time-walk," addressed under Sources of Error below. The generator and PMT were both connected to the TAC, which measured the difference in time between the generation of the pulse and the receipt of the pulse by the PMT. The PMT was also connected to a digital oscilloscope (TEKTRONIX TDS 1002) through a second anode connection, in order to maintain a reference voltage needed to counter the effect of time-walk. We read the voltage output of the TAC via the oscilloscope along with the reading from the PMT (Figure 1).
With this setup, we were able to take data over a range of varying distance parameters, denoted in the following four trials.
i) large and increasing individual Δx over large total Δx,
ii) small, constant individual Δx over small total Δx,
iii) large, constant individual Δx over large total Δx, and
iv) medium Δx with no time walk correction.
For each Δx, we moved the LED-pulse generator towards the PMT in intervals specified under Results below (Table 1).
|
|
|
Figure 1: Experimental apparatus. Light pulses initiate at the LED pulse generator, sending a start signal to the TAC. The PMT receives the pulses, creating a potential difference sent to the TAC as an end signal. The TAC generates voltage proportional to the time-of-flight of the light signals. The oscilloscope reads the voltage created by the TAC as well as the reference voltage from the PMT. In order to minimize time-walk, the PMT-polarizer unit is rotated to maintain a constant reference voltage while taking data. |
Sources of Error
Time walk was the principle source of systematic error in this experiment. It occured due to the TAC's triggering off signals from the PMT via a fixed voltage threshold. If the signal from the PMT was small, the TAC would trigger later than it would for a larger signal. In order to combat this, we used rotatable polarizers in tandem to try and maintain constant intensity of light received by the PMT. The higher the intensity, the more photons interacted with the PMT and a stronger signal resulted. The same was true in reverse.
We read the voltage amplitude from the TAC visually using cursors on the digital oscilloscope, so our measurements were not very precise. We were aided by the averaging tool provided by the oscilloscope, which helped in reading data from the oscilloscope screen.
Our device for measuring distance was a standard meterstick, whose accuracy compared to the standardized meter was not documented.
Results
| Trial 1 | Trial 2 | Trial 3 | Trial 4 (no time walk adjustment) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Table 1: Voltage readings corresponding to the time-of-flight of light pulses after each Δx. The data-taking method varied by trial: i) large and increasing individual Δx over large total Δx; ii) small, constant individual Δx over small total Δx; iii) large, constant individual Δx over large total Δx; and iv) medium Δx with no time walk correction. Note: All voltages measured with ± .02 V measurement error. All Δx measurements taken from the endpoint of the previous measurement. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Trial | Graphic Representation | Trial | Graphic Representation |
|
Trial 1:
Upper Error Bound:
Lower Error Bound:
|
|
Trial 2:
Upper Error Bound:
Lower Error Bound:
|
|
|
Trial 3:
Upper Error Bound:
Lower Error Bound:
|
|
Trial 4: (no time walk correction)
Upper Error Bound:
Lower Error Bound:
|
|
|
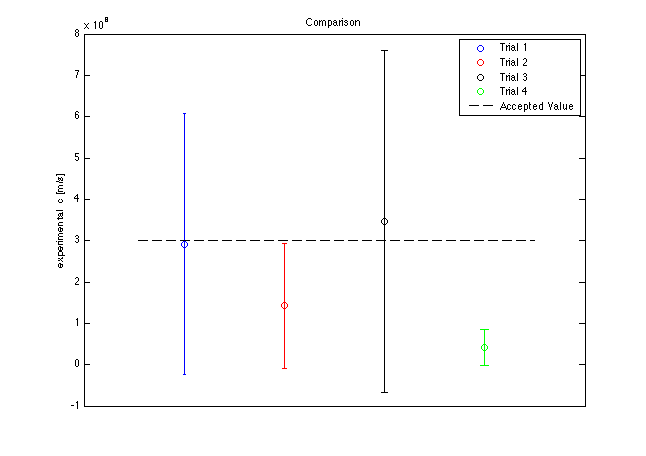
Table 2: Final experimental values and errors for the speed of light, along with corresponding graphical representations. The error range of the slope is forced through the best y-axis intercept in order to clearly show the effect of the error range from a single starting point. Assume error to be standard error according to documented least-squares analysis[11], without taking error from the oscilloscope voltage readings into account. Note: Axes are tight, so some data points are on graph edges. | |||
Measurements taken over a large individual and total Δx, as in trials 1 and 3, yielded the best results for the speed of light in air (Table 2). Unfortunately, the length of our experimental apparatus was limited, so measurements taken in consecutive movements of the meter stick limited the amount of data taken in this way. This, in turn, resulted in a large standard error. A differing method could be followed, allowing Δx measurements to be taken non-consecutively, which probably would have reduced the standard error via increased number of data. Measurements taken over small individual and total Δx as in trial 2 yielded a mean value inconsistent with the best two trials, with a standard confidence interval inconsistent with the accepted value (Figure 2). This effect is probably due to the significant amount of systematic error overwhelming the trend of light propagation observed over such a small changes in distance. Measurements taken over large total distances probably influenced the data so that the true trend could overcome systematic error unchecked in smaller-distance measurements.
|
|
|
Figure 2: Comparison of experimental results to the accepted value, by trial. SJK 17:27, 16 December 2008 (EST)Yes, I like this version of the figure a lot better. It's a great way of illustrating the results. Trials 1 and 3, corresponding to large individual and total measurements in Δx, yielded the best results. Trial 2, which measured over small individual and total Δx, yielded results outside one standard confidence interval. Trial 4 manifested a speed at least 4 σ away from the accepted value for the speed of light in air, illustrating the necessity of time-walk correction. Note: The accepted value was calculated via the refractive index of air at STP. Though the experiment was conducted at higher elevation and differing temperature, the divergence of the accepted value due to this inaccuracy is insignificant compared to the error range of the data. |
The result for trial 4 illustrates quite clearly the importance of time walk correction in this experiment. The systematic error created from neglecting this phenomenon resulted in accuracy at least 4 σ away from the accepted value. Despite a fairly precise data set, which narrowed error below that of better measurements, the final value via trial 4 is unacceptable.
Conclusion
Upon comparison with the accepted value for the speed of light in air, this experiment seems fairly sound. Correction of time-walk was essential to garnering quality data, and was the chief source of systematic error. Other sources were not thoroughly investigated, but manifested themselves in sufficient quantity to make one data trial unacceptable. The experiment could be improved further with the use of a data acquisition card or another computer interface to measure voltage from the TAC. Use of experimental controller programs such as Labview would enable highly accurate monitoring of the reference voltage, which would reduce the effect of time-walk more effectively. Individual values of TAC voltage would could be correlated with the reference voltage automatically through the program interface, so that only high-quality data would be taken. Individual voltage measurements taken this way would provide a solid data set for a more accurate statistical analysis. A higher-quality device for measuring distance would realize more precise measurements, improving statistical analysis, as well as improving accuracy via calibration to the accepted unit value of the meter.
Acknowledgements
Thanks to Miles Davis, Madonna, and Psapp, who really spiced up the data analysis. A big thank you to all the lab equipment- they're the real unsung heroes. Thanks finally to Justin, go team, Dr. Koch, go open science, and Aram, go physics!
References
-
Heyl, Paul R. "The Application of the Method of Least Squares." Science, New Series, Vol. 33, No. 859 (Jun. 16, 1911), pp. 932-933. American Association for the Advancement of Science. JSTOR
Heyl argues that the method of least-squares to average out error may be flawed, specifically in the context of extended Michelson-Morley-like experiments. He proposes a "mathematical theorem," providing a rule of thumb regarding acceptable least-squares error analysis.
-
Freedman, Hugh D.;, Roger A.; Ford, and A. Lewis Young. Sears and Zemansky's University Physics: With Modern Physics. San Francisco: Benjamin-Cummings Pub Co, 2004.
-
Heyl, Paul R. "The Present Status of the Theory of Relativity." The Scientific Monthly, Vol. 23, No. 1 (Jul., 1926), pp. 65-70. American Association for the Advancement of Science. JSTOR
Heyl reverses his opinion in his earlier cited article, outlining the experimental evidence against the existence of the aether. He makes a point of drawing attention to important experiments other than that of Michelson-Morley which led to the aether-negative consensus.
-
Hodgson, P. E. "Speed of light and relativity." Nature 271 (1978): 13. Nature
Hodgson briefly outlines the connection between special relativity and the measured speed of light, then outlines how one can show the speed of light to be independent of the speed of its source.
-
Dorsey, N. Ernest. "The Velocity of Light." Transactions of the American Philosophical Society, New Series, Vol. 34, No. 1 (Oct., 1944), pp. 1-110. American Philosophical Society. JSTOR
Dorsey covers tomes of material in this paper, including a nicely-put summary of error analysis and the least-squares approach. He analyzes a number of historical experiments measuring the speed of light and reviews their accuracy based on procedure, equipment, and effectiveness of error documentation. There doesn't seem to be any mention of confidence intervals in a standardized way, but rather each uncertainty is reported based on logical arguments and various extremum.
-
Blaney, et al., T. G. "Measurement of the Speed of Light." Nature 251 (1974): 46. Nature
Blaney et al. discuss their latest experiment in measuring the speed of light using lasers at a new frequency. Their results match others' using the same general method, as well as canonical values. They close by claiming their results as proof of the effectiveness of the laser and frequency methods of measuring the speed of light.
-
K., D. "Measuring Optical Frequencies and the Speed of Light." Nature 239 (1972): 65-66. Nature
D. K. summarizes new experiments to ascertain the speed of light using gas lamps and lasers.
-
Bureau International des Poids et Mesures. The International System of Units (SI). Brochure. 8th ed. Author, 2006. BIPM
-
Wang, L. J. "Gain-assisted superluminal light propagation." Nature 406 (2000): 277-79. Nature
Wang explores his findings in superluminal light packet propagation, in which he manipulates laser pulses through an atomic caesium gas so that their group velocities exceed c. If mentally translated to vacuum, the peak of each pulse appears to have left the gas-filled cell before entering it. He then explains that this does not supersede causality or the laws of special relativity, due to the physical intricacies of group velocity.
-
Ball, Phillip. "Going over c." Nature. Nature News. 20 July 2000. Nature News
Ball states that recent experiments challenging the fundamental theoretical moorings of the speed of light are merely bent, not broken.
-
Taylor, John R.. An Introduction to Error Analysis: The Study of Uncertainties in Physical Measurements. Sausalito, CA: University Science Books, 1996.
